埋管失稳分析的阿姆斯图兹法影响因素及应用条件

陈玮 张伟 张小飞 刘林林

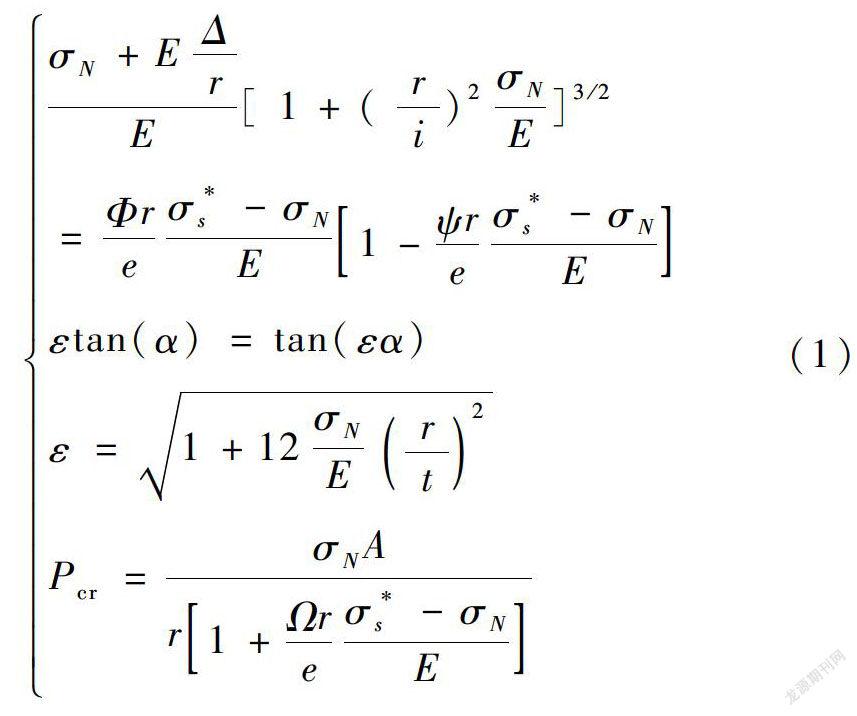
摘要：为给出埋藏式压力管道抗外压稳定分析的阿姆斯图兹法（简记阿氏法）使用建议，剖析了其临界外压计算的影响因素和应用条件。统计了阿氏法主要影响因素，即埋管径厚比、缝隙率和屈服强度的国内工程实例的数据，进而研究了这3种影响因素在工程实例范围内对阿氏法临界外压计算值的影响规律。对比了阿氏法简化公式与原公式的计算精度，结合强度破坏模式开展了阿氏法应用条件研究，给出了基于管道径厚比数值的阿氏法选用建议，并用试验数据进行了验证分析。研究表明：径厚比小于35时，需同时考虑抗外压稳定和抗外压强度校核，抗外压稳定的临界外压宜采用阿氏法原公式分析;径厚比在35～60之间时，建议采用阿氏法原公式以保证计算精度;径厚比大于60时，可采用阿氏简化公式提高计算效率。

关 键 词：埋藏式压力管道; 抗外压稳定; 阿姆斯图兹法

中图法分类号： TV732.4 文献标志码： ADOI：10.16232/j.cnki.1001-4179.2019.01.030

外压失稳是地下埋藏式压力钢管的主要破坏模式，阿姆斯图兹法（简称阿氏法）是求解抗外压稳定关键指标——临界外压的常用方法[1-2]。阿氏法基于埋管单波失稳机理给出了通过管道径厚比r/t、管道与外包混凝土间初始缝隙值Δ、管材屈服强度σs求解临界外压P cr的计算方法[3]，并已在国内外多个压力管道设计规范中推荐使用[4-7]。然而，由于阿氏法在单波失稳机理、控制方程建立、P cr求解中均存在假定与简化，应用中需要明确阿氏法的适用范围[8]，因而需要对该法的影响因素和应用条件开展研究。

一些研究者已开展了埋管P cr的影响因素研究。在r/t对P cr的影响方面：研究者已基于理论和试验研究指出了r/t与P cr 间总体呈反比关系规律;El-Sawy和Sweedan[9]、Vasilikis和Karamanos也采用有限单元法验证了该反比关系[10]。在Δ对P cr 的影响方面，Wang和Koizumi[1]、Valdeolivas和Mosquera[11]、马文亮等研究了Δ/r对P cr的影响[12]，给出在不同取值范围时的影响规律。在σs对P cr 的影响方面，Valdeolivas和Mosquera[11]、张伟等[13]、陈希等研究表明[14]，一定范围内提高可少量提高P cr 。伍鹤皋等[2]、刘启钊等[15]、Svoisky和Freishist[16]、El-Sawy也开展了阿氏法的影响因素研究，表明阿氏法P cr计算结果符合前述研究的基本规律，P cr随r/t与Δ/r增大而减小，并随σs增大而小幅增加。上述研究为合理应用阿氏法提供了良好的参考[17]，同时也可见，这些研究未分析阿氏法简化公式与原公式受r/t、Δ/r与σs的不同影响规律，也未结合影响因素的工程范围给出阿氏法的应用条件，易导致阿氏法应用不合理的问题。

鉴于此，本文基于国内外水电站埋管r/t、△/r和σs的工程统计数据，针对求解P cr的阿氏法原公式与简化公式，开展了前三者对P cr的影响规律研究，并研究了阿氏法的应用条件。

1 阿氏法临界外压计算公式与影响因素

1.1 阿姆斯图兹法临界外压计算的原公式

阿氏基于单波失稳机理，得到临界外压 P cr 的控制微分方程组，引入计算假定后，可以得到含失稳区半圆心角α、管壁环向应力σN和计算参数ε的三参数计算公式[3] ：

σN+E ΔrE[ 1+（ri）2 σNE]3/2 = Φre σ*s-σNE 1- ψre σ*s-σNEεtan（α）=tan（εα）ε=1+12 σNErt2P cr = σNAr 1+ Ωre σ*s-σNE（1）

式中，E为材料弹性模量;i为截面回转半径;e为截面管道最外纤维距中性轴距离;μ为材料泊松比，钢材可取0.3;t为管壁厚度;A为管壁截面面积;中间计算参数如下：

Φ= ε2βπδ，δ=（ε2-1）[1-cos（εα）]β= ε- 1ε[εαcos（εα）-sin（εα）]ψ= -γ4βδ，γ=ε×εα+εαsin2（εα）sin2（α）-sin（εα）cos（εα）-εsin2（εα）cos（α）Ω= -cos（εα）1-cos（εα），σ*s= Kσs1-μ+μ2K=1.5-0.51/1+ 0.002Eσs2（2）

1.2 阿氏法临界外压计算的简化公式

当 5<ε<20时，阿氏認为Φ、ψ、Ω随ε变化较小，可取ε=20 时的数值：

Φ=1.73，ψ=2.25，Ω=0.175（3）

将式（3）代入式（1），得到阿氏法 P cr  简化公式：

12ri2 σN+E Δrσ*s-σNσNE 3/2 =1-0.45 rt σ*s-σNE

P cr = tσNr 1-0.35 rt σ*s-σNE（4）

将管道参数r/t、Δ/r与σs代入式（4）求得P cr ，该公式无需迭代计算，便于工程应用，被多国规范采用。

1.3 临界外压影响因素及其工程范围

由式（1）与式（4）可见， r/t、Δ/r和σs是采用阿氏法计算P cr  的主要影响因素，即：

P cr =frt， Δr，σs（5）

本文充分调研国内外实际管道工程274组数据后， 得到r/t、Δ/r和σs的工程范围统计数据，见图1。

从图1可见，r/t工程范围介于25～300之间;Δ/r主要介于（0～14）×10 -4 之间，个别达到55×10 -4 ;σs介于225～700 MPa之间，300 MPa级的16 Mn钢此前应用相对广泛。

2  r/t、Δ/r和σs对临界外压的影响规律

2.1  径厚比r/t的影响

假设管道材料采用16Mn钢，取325 MPa，分别用阿氏原公式与简化公式计算r/t在典型工程范围内的埋管P cr ，同时给出了阿氏法简化公式相对原公式的偏差，见图2。

由图2（a）和2（b）可见，P cr 计算值随着r/t增加呈不断减小趋势，这一规律与以往试验结果和分析结果相同。此外，由图2（c）也可见，简化公式得到的P cr 整体较原公式结果偏小，尤其当r/t<60时，偏差可达10%，因此建议对于这类r/t较小的管道采用原公式求解P cr 。同时也可见r/t≥60时，简化公式与原公式的偏差较小，可以采用简化公式计算P cr 。

2.2 缝隙率 Δ/r的影响

管道材料采用16Mn钢，σs取325MPa，分别用阿氏原公式与简化公式计算Δ/r在典型工程范围内的埋管P cr ，计算结果如图3。

由图3（a）和3（b）可见， P cr 计算值随着Δ/r增加呈减小趋势，且减小幅度不大。此外，由图3（c）也可见，简化公式得到的P cr 整体较原公式结果偏小，偏差η基本在5%以内，可以采用简化公式计算P cr 。

2.3 屈服强度 σs的影响

考虑工程范围内Δ/r的影响不大，忽略其影响，分别采用阿氏原公式与简化公式计算埋管σs对P cr 的影响，计算结果如图4。

由图4（a）和4（b）可见，当r/t较小时，P cr 随着σs的增大而明显增加;r/t增大，σs对P cr 的影响逐渐减小，r/t>200时对P cr 的影响基本可以忽略，即提高材料强度不能增加埋管抗外压稳定能力。此外，由图4（c）也可见，简化公式得到的P cr 整体较原公式结果偏小，η随σs增大而减小，但η在2.5%以内，可以采用简化公式计算P cr 。

3 阿氏法临界外压计算公式的应用条件

3.1 阿氏法简化公式的应用条件

由图2（c）、3（c）和4（c）可知，阿氏法简化公式相对原公式存在偏差，偏差η主要与r/t和Δ/r有关，也受σs影响，以偏差η=5%作为简化公式可应用的判别标准，得出σs分别取325，450 MPa和700 MPa时的应用条件，如图5。左上方区域表示简化公式较原公式误差超过5%的部分，右下方则为误差在5%以内的部分。

由图5可以判断阿氏法原公式与简化公式计算P cr 的应用条件，当点（r/t，Δ/r）落在简化公式应用边界左侧，η>5%，建议使用阿氏法原公式计算P cr 以保证精度;当点（r/t，Δ/r）落在简化公式应用边界右侧，η<5%，可以使用阿氏法简化公式高效计算P cr 。同时，阿氏法简化公式的适用范围随σs的增大而增大。

3.2 阿氏法稳定破坏的应用条件

当管道结构r/t和Δ/r较小时，外水压作用可能先使管道发生强度破坏，而不是外压失稳破坏，若以管壁受压屈服作为强度破坏的判定标准，不发生外压强度破坏的极限外压Pl为

Pl= σstr（6）

以Pl=P cr 作为阿氏法可应用的判别标准，得出σs分别取325，450 MPa和700 MPa时的应用条件见图6。图中同时也给出了阿氏法原公式和简化公式的应用条件。

由图6可以判断管道发生强度破坏和稳定破坏的应用条件为：当点（r/t，Δ/r）落在强度破坏边界左侧时，管道发生强度破坏，需使用式（6）计算Pl，进一步开展管道强度设计与安全评价;当点（r/t，Δ/r）落在强度破坏边界右侧，管道发生稳定破坏，可使用阿氏原公式或简化公式计算P cr ，進一步开展管道抗外压稳定设计与安全评价。

同时可见，强度破坏区域随钢材强度增加显著小，σs在450MPa以下时，r/t约在30以下时发生强度破坏，而σs达700 MPa时，不存在强度破坏区域。需要说明的是，如取允许应力，则强度破坏区域将会显著增加，按埋管基本荷载膜应力区安全系数1.5考虑时[5-18]，阿氏法应用条件如图7所示。

由图7可见，考虑安全系数后，Δ/r=0时，为325，450MPa和700 MPa时发生强度破坏的r/t边界分别为60，47和33，r/t低于该边界时需按强度破坏进行设计与评估，超过该强度破坏边界时按阿氏简化公式求解P cr ，并进一步进行抗外压设计与评估。需要注意的是，由于工程实际中Δ/r数值难以量化，因此当管道r/t在图7强度破坏边界左侧时， 宜同时进行强度和稳定性分析，稳定性分析的P cr 建议采用阿氏法原公式求解。

4 影响规律和应用条件的试验验证

根据搜集到的埋藏光面管试验数据，比较临界外压P cr 试验值与阿氏法原公式和简化公式计算值的结果，并给出各公式偏差在不同r/t范围内的均方根RSM，以此反映各公式计算值与试验值的接近程度。RSM越小，计算值与试验值越接近，见图8。

由图8可见，3560时，阿氏原公式、简化公式与试验P cr 的RSM一致，说明此时使用简化公式计算P cr 能保证精度，故可采用简化公式提高计算效率。

5 结 论

研究了埋藏式压力管道抗外压稳定分析的阿姆斯图兹法的影响因素及应用条件，得出以下结论。

（1） 埋藏光面管临界外压P cr 的主要影响因素是r/t、Δ/r和σs。其基本影响规律为：P cr 随r/t与Δ/r增大而减小;P cr 受σs的影响相对前两者较小，r/t>200时σs对P cr 的影响基本可以忽略;同时，P cr 在r/t较小时，也需考虑强度破坏模式的影响。

（2） 对国内外水电站压力钢管工程调研表明：r/t工程范围介于25～300之间;Δ/r主要介于（0～14）×10 -4 之间，个别达到55×10 -4 ;σs主要介于225～700MPa之间。

（3） 给出了不同r/t、Δ/r和σs时的阿氏法P cr 计算公式应用条件。偏安全地考虑，当r/t小于35时，需同时考虑外压稳定和强度校核，外压稳定宜采用阿氏原公式分析;当r/t在35～60之间时，推荐采用阿氏原公式以保证计算精度;当r/t大于60时，推荐采用阿氏简化公式提高计算效率。

参考文献：

[1]Wang J H，Koizumi A. Experimental investigation of buckling collapse of encased liners subjected to external water pressure[J].Engineer Structures，2017（151）：44-56.

[2]伍鹤皋，周彩荣，付山，等.埋藏式压力钢管加劲环抗外压稳定分析方法探讨[J].水力发电学报，2015，34（12）：19-23.

[3]Amstutz E.Buckling of pressure-shaft and tunnel linings[J].Water Power，1970，22（11）：391-400.

[4]ASCE 79-2012.ASCE manuals and reports on engineering practice No.79 “Steel penstocks （second edition）”[S].Virginia： American Society of Civil Engineers，2012.

[5]NB/T35056-2015 水電站压力钢管设计规范[S].北京：中国电力出版社，2015.

[6]Technical Standards for Gates and Penstocks （2007 Edition）[S].Tokyo：Technical Committee of Hydraulic Gate and Penstock Association of Japanese，2007.

[7]ATV-M 127-2.Structural Analysis for Rehabilitation of Sewers and Pipelines by Lining and Reassembling Methods[S].Hennef： German Water Association，2000.

[8]张伟，刘林林，陈玮，等.埋藏光面管抗外压稳定分析的阿姆斯图兹法及其应用研究[J].广西大学学报：自然科学版，2017，42（4）：1561-1571.

[9]Khaled M El-Sawy，Amr M I Sweedan.Elastic stability analysis of loosely fitted thin liners-A proposed simplified procedure and evaluation of existing solutions[J].Tunneling and Underground Space Technology，2010，25：689-701.

[10]Daniel Vasilikis，Spyros A. Karamanos.Stability of confined thin-walled steel cylinders under external pressure[J].International Journal of Mechanical Sciences，2009（51）：21-32.

[11]Valdeolivas J L G，Mosquera J C.Three-Dimensional FEM Parametric Analysis of Stiffened Steel Liners in Hydroelectric Pressure Tunnels[J].Journal of Pipeline Systems Engineering and Practice，2016，7（1）：04015019.

[12]馬文亮，刘东常，刘桂芳，等.考虑初始缝隙因素作用钢管抗外压稳定计算的一种半解析有限元法[J].华北水利水电学院学报，2005，26（1）：31-34.

[13]张伟，杨江琪，李伟.考虑初始缝隙的埋藏式光面管临界外压经验公式[J].人民长江，2016，47（14）：60-63.

[14]陈希，郑津洋，缪存坚，等.应变强化后容器的外压屈曲分析[J].压力容器，2015，32（8）：14-20， 6.

[15]刘启钊，谈为雄，刘焕兴，等.埋藏式钢管外压稳定计算[J].水利水电技术，1980，11（2）：29-39.

[16]Svoisky F M，Freishist A R.External pressure analysis for embedded steel penstocks[J].Water Power&Dam Construction，1992，44（1）：37-43.

[17]Khaled M El-Sawy.Inelastic stability of liners of cylindrical conduits with local imperfection under external pressure[J].Tunneling and Underground Space Technology，2013，33：98-110.

[18]SL 281-2003 水电站压力钢管设计规范[S].北京： 中国水利水电出版社，2003.

引用本文：陈 玮，张 伟，张小飞，刘林林.埋管失稳分析的阿姆斯图兹法影响因素及应用条件[J].人民长江，2019，50（1）：163-169.

Influential factors and application conditions of Amustutz′smethod for evaluation of critical external pressure of embeded pipe

CHEN Wei 1，2，3 ，ZHANG Wei 1，2，3 ，ZHANG Xiaofei 1，2，3 ，LIU Linlin4

（1. School of Civil Engineering and Architecture，Guangxi University，Nanning 530004，China; 2.Key Laboratory of Disaster Prevention and Structural Safety of China Ministry of Education， Guangxi University，Nanning 530004，China ; 3.Guangxi Key Laboratory of Disaster Prevention and Engineering Safety，Guangxi University， Nanning 530004，China;4. Shandong Bureau of Yellow River，Jinan 250011，China）

Abstract：To give reasonable application recommendations of Amustutz′s method （AM） in buckling analysis for embeded pipe， the influential factors and application conditions in evaluation of critical external pressure were illuminated. Statistics on the domestic and abroad engineering sectors of AM′s main influential factors， i.e. radius-thickness ratio， gap ratio and yield strength of tunnel linings were collected. The influences of the three factors on AM′s results were clarified in practical cases. The calculation accuracy of AM′s simplified formulas was compared with that of original formulas， and application conditions were analyzed considering strength failure mode. The application recommendations of AM were given in term of radius-thickness ratio and verified by experiment. It can be concluded that the performance against buckling and anti-external pressure strength should be checked when the radius-thickness ratio is less than 35， and the AM′s original formulas are suggested in the buckling check. The AM′s original formulas are also suggested for ensuring the calculation accuracy when the radius-thickness ratio is 35 to 60， and the AM′s simplified formulas are suggested when the radius-thickness ratio is larger than 60.

Key words： buried pressure pipeline; anti-external pressure stability; Amstutz′s method