“物理模型与建模”在高中生物教学中的应用
郭卫华
摘 要:伴性遗传发病率和能量传递一直以来都是高中生物中的重难点及高考中的高频考点.教学中通过构建简易物理模型,既有利于重难点的突破,又能激发学生的学习兴趣,真正将“做中学”落实到课堂中.
关键词:伴性遗传;能量传递;物理模型
物理模型在高中生物学习中常被提及,在教学中构建生物学模型有助于学生系统地、完整地学习和理解新知识,更有助于学生运用生物学模型去解决生物学问题[1].教学中笔者首先通过抽奖游戏将“抽象问题具体化”,把难以把握又存在复杂关系的伴性遗传发病率的问题,转变成直观的具体问题让学生去思考;再运用“剪切”纸片方式构建纸片模型,清晰再现了能量传递的过程.构建两次物理模型,帮助学生突破难点的同时,显著提高了学生的有意注意和参与度,促进学生小组讨论与合作学习,大大提高了课堂学习的效率.
1 构建“抽奖模型”突破伴性遗传发病率计算
1.1 抽奖模型的构建
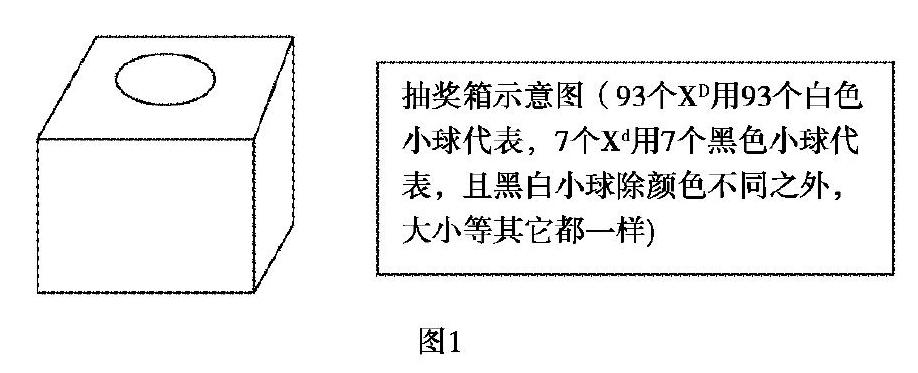
(1)抽奖箱设计:先以伴X隐性遗传病为例,Xd为致病基因,构建抽奖箱(如图1).具体方法是:用一个不透明的纸箱,上方挖一个仅可以伸进手的小洞,纸箱中放入93个白色小球(代表93个XD基因),7个黑色小球(代表7个Xd基因).奖箱中的XD基因与Xd基因的比例代表人群中XD基因与Xd基因的比例.
(2)抽奖原则及程序:女生有两条X染色体,抽两次奖组合在一起代表其基因型.男生只有一条X染色体,故只抽一次,然后与Y染色体组合在一起代表其基因型.抽奖程序为:①抽奖者先将手放置在抽奖箱口,但不要放入;②抽奖前闭眼,然后由抽奖监督员摇晃奖箱3次;③抽出一个球展示给记录员,做好记录;④每次抽奖后再将球放回原奖箱.最后,统计全班男生和女生的“发病率”,进行比较.
1.2 理论计算
依据构建的抽奖模型,让学生从理论上计算出男女各自的发病率.对于伴X隐性遗传病,假设人群中Xd基因占7%,XD基因占93%,则男性因只有1条X染色体,故只有一次抽奖机会.男性中患者(即抽到Xd基因的概率)占7%,男性中正常(即抽到XD基因的概率)占93%.女性中患者XdXd的比例(即为两次均抽到Xd基因的概率)为7%×7%=0.49%,正常的概率为1-0.49%=99.51%.由此不难看出,在伴X隐性遗传病中,男性的发病率高于女性,人群中的男患者多于女患者.
1.3 类比法-自主计算伴X显性遗传病男女发病率
假设人群中XE基因占7%,Xe基因占93%,XE为致病基因.请依据抽奖模型,分别计算出男性和女性的发病率.要求学生先独立计算,再小组讨论交流,最终,各小组派代表展示本组结果:男性因只有1条X染色体,故只有一次抽奖机会,男性中患者(即抽到XE基因的概率) XEY为7%,男性中正常(即抽到Xe基因的概率) XeY为93%.女性中正常XeXe的比例(即为两次均抽到Xe基因的概率)为93%×93%=86.49%,女性中患病的概率则为1-86.49%=13.51%.由此不难看出对于伴X显性遗传病,女性的发病率高于男性,在人群中女性患者多于男性患者.
1.4 小组讨论、比较与分析
为什么实际抽奖得到的统计概率不论是X隐性或X显性与计算得出的理论数据之间差距较大?如何才能让实际抽奖得到的统计概率更为贴近理论数据呢?通过小组讨论,活跃学生思维,促进合作学习.通过各小组代表发言、展示,最后得出结论:抽奖次数太少导致偏离理论值.如果把整个年级共18个班的数据(甚至全校所有年级的数据)分别集中在一起,再展开讨论,学生对伴性遗传病男女发病率不同的原因就有了比较定量的、深刻的理解.并认识到统计性状分离比时,数据要尽可能地多,这样理论值和实际值才能更接近.
2 构建纸片模型,再现能量传递过程
2.1 “剪切”纸片—确定不同营养级的同化量
2.1.1 创设问题情境
生态系统中能量是通过食物链和食物网的渠道传递.不同颜色的纸片来代表不同营养级,纸片的大小可表示能量的多少[2].教学中为方便交流,规定统一用绿纸片代表生产者同化的能量、用黄色纸片代表初级消费者同化的能量、用红色纸片代表次级消费者同化的能量.
2.1.2 学生活动
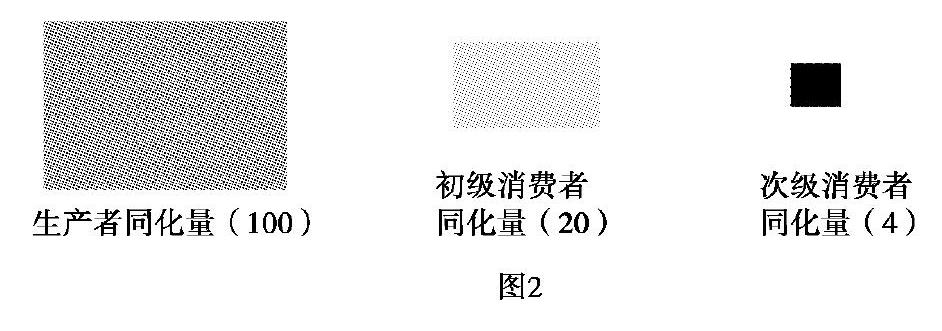
如果以能量传递效率20%计算,可构建生产者(100=10×10)、初级消费者(20=4×5)、次级消费者(4=2×2)的纸片模型(如图2).
同理,如果以能量传递效率10%计算,可构建生产者(100=10×10)、初级消费者(10=2×5)、次级消费者(1=1×1)的纸片模型(此处略),三级消费者由于同化的能量值较小,用纸片表示比较困难.
2.2 “拆分”纸片—确定能量的来源和去路
2.2.1 创设问题情境
生产者固定的太阳能是流经该生态系统的总能量,生产者同化的能量只有一部分传递给了初级消费者.根据能量守恒定律,其他的能量到哪里去了?请在大小合适的纸片上写上能量的去路.
2.2.2 学生活动
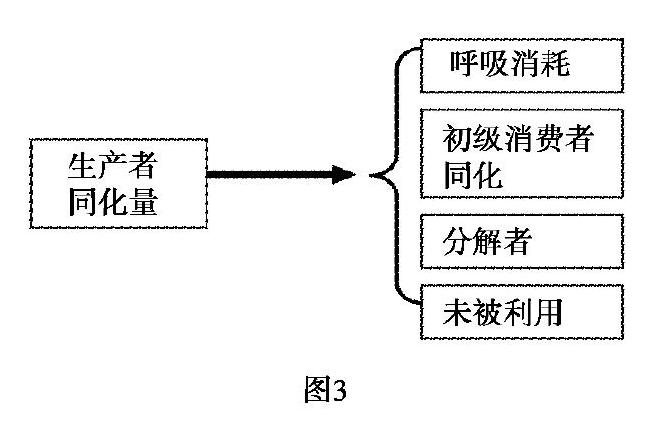
学生讨论和查阅教材后得出,生产者同化的能量,一部分在呼吸作用中以热能的形式散失,另一部分储存在植物体内.储存在植物体内的能量,一部分随着植物体的衰老死亡以枯枝落叶的形式被分解者分解而散失,一部分会通过初级消费者的取食而流入初级消费者,还有一部分未被利用.学生列出如图3所示的能量去路图.
2.3 “回拼”纸片—确定能量之间的关系
生产者同化的能量,除了呼吸消耗、初级消费者同化和分解者分解这3条途径之外,还有部分能量未被利用,根據能量守恒定律,这4个纸片的大小总和应该等于生产者同化量纸片的大小.将这4个纸片贴回到代表生产者同化能量的纸片中(如图4).
同理,初级消费者同化的能量也可以分成4个部分,也可以进行回拼,这里就不再赘述.通过回拼图片的过程,学生能够理清这个基本等式:每一营养级同化量=自身呼吸消耗+下一营养级同化+分解者分解+未被利用.
通过构建纸片模型,可加深学生对过程、规律的理解.在能量流动教学中,选用彩色纸片制作物理模型,一方面是因为纸片易于剪裁和粘贴,便于再现能量流动的过程;另一方面是因为彩纸颜色丰富,更易区分,便于帮助学生区分能量值之间的关系.用纸片模拟生态系统中能量流动过程,能够给学生新的刺激情境,学生在这个情境中可利用已有的图式或认知结构,通过逻辑思维和推理把动态拼图的过程整合到认知结构中,把外在的知识内化为自己的知识,实现知识的同化和加深[3].
生物学是一门以实验为基础的科学,由于受到主客观因素的限制,像遗传病发病率及生态系统能量流动的过程等在高中阶段难以通过实际实验进行观察和数据统计.教学中通过构建简易物理模型,既可激发学生学习兴趣、给学生新的刺激情境;又能化繁为简、很好地将重难点突破;真正将“做中学”落实到课堂中,保证课堂教学效果.
参考文献:
[1]夏祥斌. 在高中生物学教学中应用模型构建化解抽象问题[J].生物学教学,2012,37(12):19-21.
[2]张纯,唐晓春,冯瑶琼.“能量流动”物理模型的构建与应用[J].中学生物教学,2018(23):14-15.
[3]张德超,赵苹.生物教学中能量流动的理解误区与阐释[J].教学与管理,2017(28):58-59.
(收稿日期:2019-11-25)

