一道中考几何压轴题的解析与教学启示
范鸿
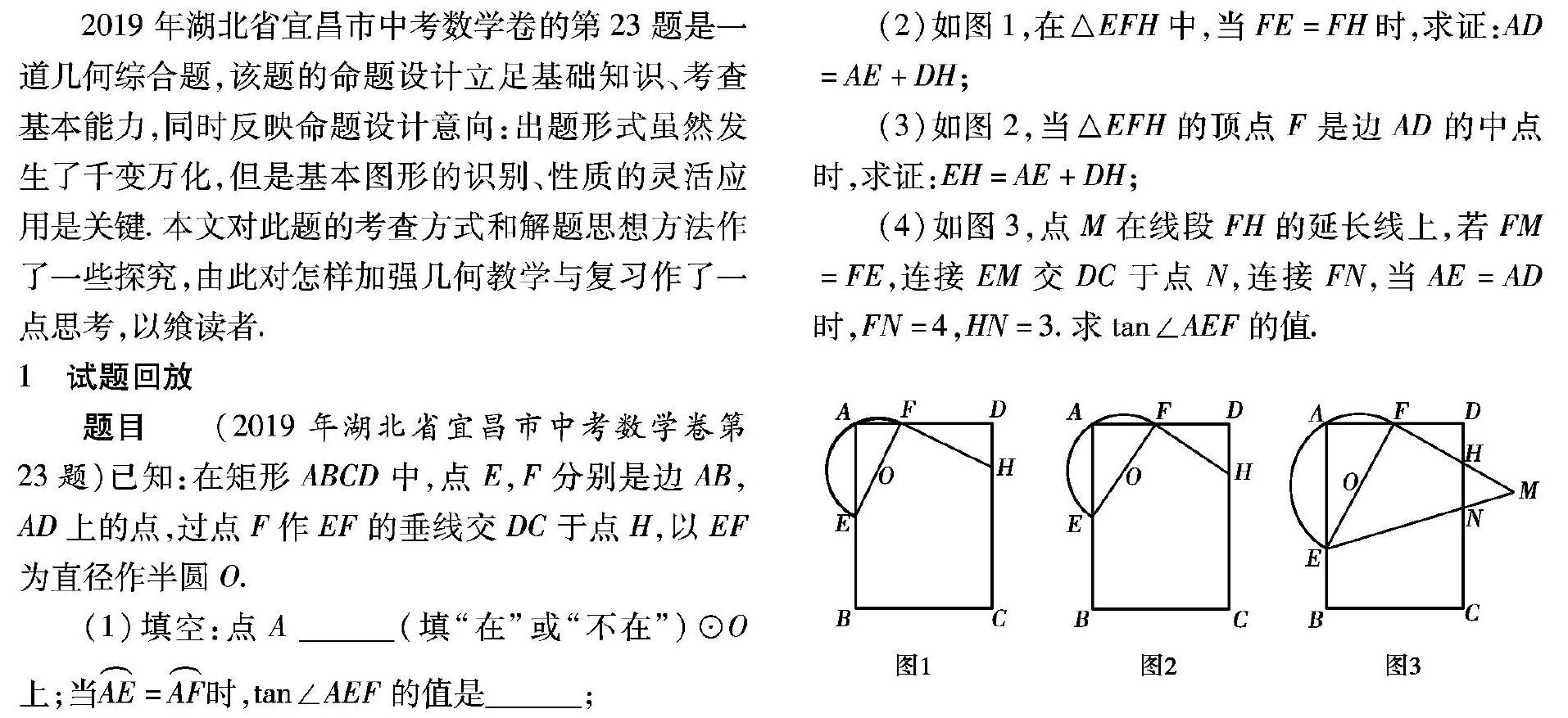

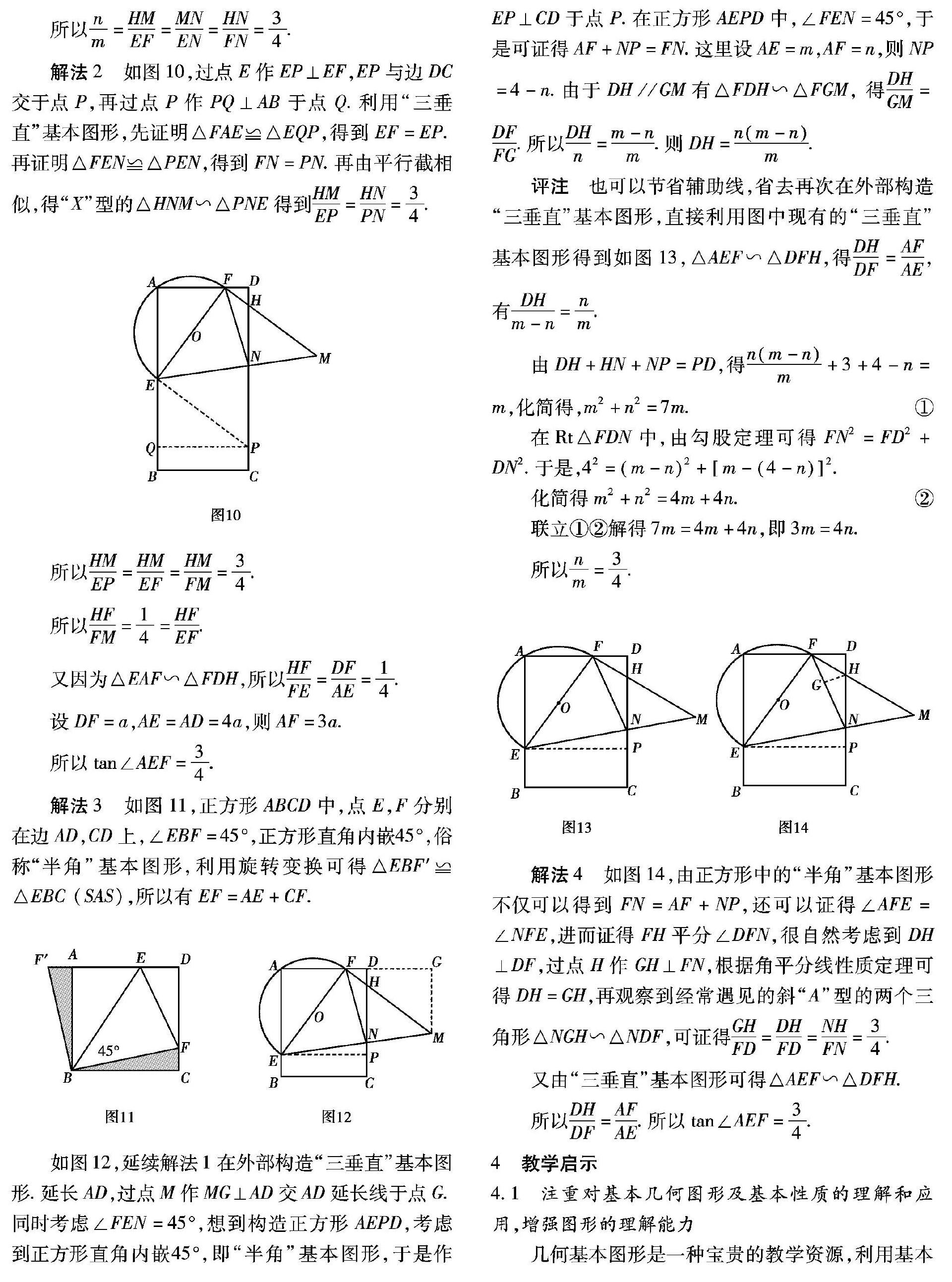
摘 要:中考几何压轴题往往都是由几何基本图形构成的,如果学生对基本图形的结构以及结论非常熟悉,就会启迪分析问题的思路,激发智慧的火花,从而快速找到解决问题的办法.本文以一道中考几何压轴题的教学为例,引导学生通过分类、比较、辨析、探究,认识图形本身的基本性质,以及图形之间的联系和区别,形成清晰的知识网络,提高图形的分析能力.
关键词:基本图形;几何;解析
4.2 注意积累并传授学生几何基本图形的变式思路
经常用到的是改编几何基本图形的问题背景,拓宽问题的生成空间.通过改变问题的呈现方式、改变问题条件、拓宽命题的结论去设置问题、加深问题的思考角度等方式,充分体现基本图形的价值,为几何题的命制创造广阔的空间.例如问题在形内成立,在形外是否成立?问题对特殊性成立,对一般性是否成立?是否可以把平面几何问题放到直角坐标系中研究等等.具体来讲,有以下几何基本图形的变式思路可供借鉴:
(1)原有图形的一些结论在图形适当运动变化以后仍然成立,或者做适当调整后得到类似的结论,实现对知识的迁移和能力的提升;
(2)将问题的背景设置在平面直角坐标系中,通过坐标将数与形有机地结合起来,拓宽知识的认知空间和深度,达到既考查几何问题,又渗透函数的思想与理念的目的;
(3)从辅助线添加的角度,获得对几何基本图形的逆向认识和深入思考;
(4)将几何基本图形结论隐藏起来,设置动手操作过程,让学生体验知识的来龙去脉,在操作过程中发现问题并给出证明.
4.3 关注图形问题中蕴含的数学思想和方法,提升数学素养
数学思想和方法是数学知识的有机组成部分,是知识转化为能力的桥梁.教学中,一方面,要引导学生深入理解基本图形及其性质,使学生掌握必要的基础知识;另一方面,更要通过几何图形这个载体,挖掘其中蕴含的数学思想方法,如数形结合、分类讨论、函数建模、方程建模等等,促使学生更好地理解图形、感悟图形,形成正确的图形观和一定的图形意识.事实上,单纯的知识教学,只显见于学生知识的积累,是会遗忘甚至于消失的,而方法的掌握、思想的形成,才能使学生受益终生,正所谓“授之以鱼,不如授之以渔”.
参考文献:
[1]赵军才,薛红霞.2011年中考数学试题分类解析——空间与图形[J].中国数学教育,2012(Z1):50-65.
[2]鄒守文,王俊.一道经典几何题向中考试题的演变[J].中国数学教育,2012(05):37-39.
(收稿日期:2019-11-20)

