桩锚基坑支护锚索位置优化分析与探讨

郭锐剑，段 建，俞 莉，周文权，母海鹏，黄佳梅

(1.湖南工程学院 建筑工程学院，湘潭 411104；2.兰州理工大学 土木工程学院，兰州 730050；3.中都工程设计有限公司，成都 610041)

0 引言

桩锚支护技术因占用地少、整体稳定性好，且能有效约束变形等特点，已在基坑工程中得到了广泛运用；同时，随着当前城镇化建设的不断深入推进，城市建设用地日趋紧张，必将涌现诸多规模更大更深、周边环境更为复杂的深基坑市场.鉴于桩锚支护技术突出优势与深基坑建设需求，开展其支护理论与应用研究已迫在眉睫.目前，国内外学者对此开展了一些相关研究工作，如肖宏彬[1]等针对深基坑开挖中广泛采用的多支撑挡土结构，考虑分步开挖的施工过程对支撑反力、挡土结构内力和位移的影响，提出了以弹性地基梁理论为基础的多支撑挡土结构开挖过程的有限元分析方法，并推导出了各开挖阶段矩阵方程的形式.冯紫良[2]等提出了一种新型的单元模型来模拟桩锚结构，推导了锚桩工作状态下接触面处的位移解答和刚度公式，编写了有关的计算程序.晏鄂川[3]等利用结构力学理论，在研究桩锚结构体系的两阶段变形过程的基础上，对桩锚结构变形协调方程进行了改进，包括改变原有方法中抗滑桩滑面处位移和转角的计算方法以及改变第j排锚索对桩身i点处位移贡献的计算形式.丁敏[4]等采用将桩锚结构视为荷载作用-侧向弹簧支承的连续梁模型，支护桩为直立的弹性地基梁，主动土体转换为土压力，锚杆简化成为可逐步施加的弹簧支承，而被动土体则用侧向支承的土体弹簧替代，以此提出了以矩阵分析为手段的桩锚结构分析方法.张敏[5]等在传统的三点定圆法、最小二乘法、自然样条法反算弯矩的基础上提出了改进的最小二乘法和改进的自然样条法，并利用两种方法反演支护桩弯矩.陈涵[6]等运用MIDAS GTS NX，数值分析预应力锚杆和普通注浆锚杆组成的桩锚支护结构力学变形之差异，认为相比普通注浆锚杆而言，预应力锚杆具有较好的限制变形能力.黄明辉[7]等采用有限元软件MIDAS/GTS NX，建立桩锚支护结构三维仿真模型，探讨锚杆安置倾角作用机理，发现支护结构变形在一定倾角范围内出现谷值，存在最优安置角范围.等等，这些都大大丰富了桩锚支护技术理论基础与工程应用，为工程设计提供了一定的指导意义.然而，该技术涉及结构与岩土体的相互作用，与周边环境也相互制约，影响因素甚多，研究难度大，其相关支护理论、施工技术等目前还不够完善，远跟不上工程实践的步伐，在当今城市建设日趋密集的环境下，常常出现一些基坑失稳垮塌事件，相关报道也屡见不鲜，由此，加强此方面的研究尤显重要.

为此，本文以实际工程为依托，在保证基坑稳定和其他条件相同的前提下，仅通过调整锚索位置，对基坑进行多次试算[8-9]，在深入分析桩身内力和基坑变形变化规律的基础上，探讨合理的锚索布置方案，以期为类似工程提供借鉴.

1 工程概述

拟建项目为长沙黄花综合保税区进出口商品展示交易中心，位于市经济技术开发区，该建筑地上6层，地下2层，框架剪力墙结构，项目全貌如图1所示.该场地地势平坦，四周依次临接已建黄金大道、巡逻路、停车场与大元路，基坑周边环境复杂，且不具备放坡空间.

图1 拟建建筑鸟瞰全貌

1.1 场地工程地质条件

场地揭露地层依次为人工填土、粉质粘土、强风化泥质粉砂岩与中风化泥质粉砂岩，其中西侧原为水塘，地形地貌由近期人工填筑所形成，表层人工填土较深，厚约10 m.各地层物理力学参数如表1所示.场地地下水为上层滞水，赋存于人工填土及第四系粘性土中，其在丰水期主要受大气降水补给，在枯水季节则直接被蒸发，水位变化直接受气候条件变化的影响；场地内各地层均为弱透水层.场地西侧工程地质情况如图2所示.

图2(a) 场地西侧工程地质概貌

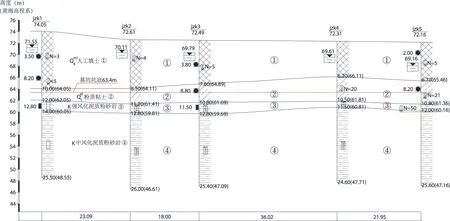
图2(b) 场地西侧工程地质概貌

表1 岩土体物理力学参数

考虑到西侧基坑人工填土深厚，工程地质条件差，且基坑顶边线距离征地红线仅3 m，坑顶又选做施工料场，致使该侧基坑开挖所形成的土质边坡变形难以控制，极易失稳滑塌，本文旨以西侧基坑支护进行锚索位置优化探讨，以期为工程施工提供计算依据与理论指导.

1.2 研究方案的拟定

西侧基坑为一级基坑，拟采用排桩+预应力锚索支护形式，总体布置如图3所示.通过计算分析，发现锚索竖向位置对基坑支护工作性能影响较大，为了探明两者间的相互关系，设置基本条件为：坑深取10.65 m，排桩桩径为1.2 m，桩间距为2 m，桩嵌固段长5 m，锚索入射角为30°，坑顶设计荷载取30 kPa，锚索横向布置于桩间土上(设置冠梁与钢腰梁)，竖向共布置3排，从上至下每排锚索施加预应力为：480 kN、380 kN、300 kN，且计算中满足基坑整体稳定性等各项指标要求.考虑工程造价及变形限制等因素，在其他设计参数不变仅调整锚索竖向位置情况下，分析锚索竖向位置(h,d)对桩身内力(弯矩Mmax和剪力Qmax)、桩顶水平位移Δx与坑顶地表沉降ω的影响，从而提出工程最优设计方案.

为此，锚索的竖向布置研究方案分两个层面：①第一排锚索距桩顶距离h为1.0 m、1.5 m、2.0 m和2.5 m 4种情况；②锚索间竖向间距d分成2 m、2.25 m、2.5 m、2.75 m、3.0 m和3.25 m 6种情形.

图3 西侧基坑支护方案

2 桩身内力与锚索位置关系

依据上述基本条件，计算获得桩身最大弯矩、剪力与锚索位置关系如图4所示.

图4 桩身内力与锚索布置关系

当第一排锚索位置h一定、仅改变锚索间距d时，桩身最大弯矩Mmax随间距d的增大而减小，如图4(a)所示，当锚索间距小于2.75 m时，每增加0.25 m索间距，弯矩减小值为100～140 kN·m，即：锚索间距在某一范围内，索间距的增大与弯矩的减小基本呈线性关系，表现为前半段直线下降特性；而当锚索间距大于2.75 m时，随着锚索间距的增加，弯矩的减小幅度下降，且其减小值与第一排锚索位置有着密切联系，在此区间，当第一排锚索与桩顶距离为1 m、1.5 m、2 m、2.5 m时，每增加0.25 m的锚索间距，弯矩的平均减小值分别为120 kN·m、71.5 kN·m、67.6 kN·m、5.4 kN·m，说明当锚索间距大于某一限值时，增大锚索间距不能显著减少弯矩，且随着锚索总体位置的下移，弯矩值随锚索间距的变化敏感性降低，体现在图4(a)中的曲线越往下越平缓，甚至最下面的曲线出现不降反升的趋势；出现该现象主要是由于锚索间距较大时，使得最下一排锚索与基坑底距离较近，其所分担的土压力减小，参与受力工作程度不高，致使桩身弯矩没有明显减小，尤其是当第一排锚索与桩顶距离为2.5 m时，上部两排锚索承担了较大的土压力，桩身弯矩不减而反升.同时，在锚索间距一定、仅改变第一排锚索位置h的情况下，第一排锚索与桩顶的距离每增大0.25 m，其弯矩减少值为200 kN·m左右，如图4(a)可见四条曲线平行且间距基本相等.由上述分析可见，将第一排锚索下调0.25 m比扩大锚索间距0.25 m所减少的弯矩更多，敏感性更高.在工程中，弯矩决定了桩身纵向受力钢筋数量，直接影响工程造价，可通过上述规律调整锚索位置确定弯矩值，从而获得经济安全的最优设计方案.

剪力值决定了桩身箍筋数量，此指标也是制约工程造价重要因素之一，图4(b)曲线描述了锚索布设方案与桩身剪力之间的对应关系，总体上，剪力图和弯矩图形态基本相似，体现为两个特征：

(1)四条曲线的前半段均成线性关系，后半段越来越平缓.在前半段的直线区段内，锚索间距每增大0.25 m，剪力的减少值约为30 kN，直线段基本平行且间距相等；在后半段的非线性段内，锚索间距每增大0.25 m，剪力的减少值平均不到10 kN，减小值显著变小，甚至出现不降反增的趋势.

(2)当第一排锚索距桩顶1 m时，锚索间距从2 m增大到3.25 m，锚索间距每增大0.25 m，剪力值减小值分别为26.13 kN、26.43 kN、22.81 kN、24.56 kN和5.23 kN，仅在锚索间距达到3.25 m时，剪力减小幅度显著降低；而当第一排锚索距离桩顶2.5 m时，同样情况下的剪力减小值分别为28.19 kN、27.34 kN、-17.96 kN、-5.14 kN、16.57 kN，仅仅在桩间距为2 m和2.5 m时保持线性比例关系.由此可见，剪力随着锚索总体位置的下移，对锚索间距的增大越来越不敏感，在图中表现为从上往下曲线的平缓段明显增长，与弯矩图相比较，这种特性剪力图表现得更为明显.

通过上述桩身内力与锚索位置关系分析可知，弯矩、剪力-锚索位置关系图特征相似，都呈现出直线段和非直线段，且直线段的间距基本相等，说明在该段内力值与锚索间距、第一排锚索距桩顶距离均成比例关系；当锚索整体偏下时，曲线图则出现非直线段，在该段内，锚索间距的增大和第一排锚索的下移均不会使内力值明显减小，且当锚索间距过大，锚索整体位置下移可使曲线的平缓段增长.因此，在工程实际当中，当锚索总体位置偏上时，在一定范围内调整锚索的间距可使桩身内力按比例变化，而当锚索总体位置偏下时，不宜使锚索间距太大，使得布设的各层锚索均能充分发挥材料强度，桩与锚索共同受力工作，使其工作性能达到最佳；同时，调整第一排锚索位置比调整锚索间距对桩身内力的影响更大.

3 变形与锚索位置关系

桩锚支护体系变形控制指标一般以桩顶水平位移Δx和坑顶地表沉降ω来衡量，图5、图6分别给出了其与锚索位置关系.

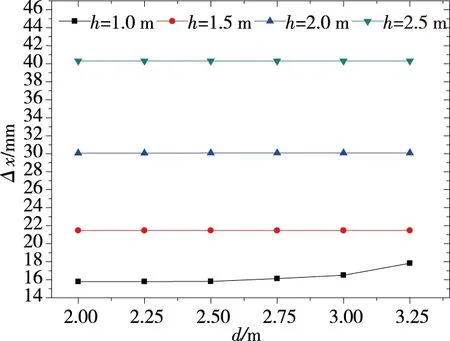
图5 桩顶水平位移与锚索布置关系

图6 坑顶地表最大沉降与锚索布置关系

由图5可知，桩顶水平位移随着第一排锚索与桩顶的距离h的增大而增大，与锚索间距d大小影响甚微，仅当第一排锚索距离桩顶距离为1 m时，桩顶水平位移随着锚索间距的增大而有稍许增大趋势，且其增量值在工程中可以忽略不计，在实际工程中，锚索离桩顶太小会形成一定的施工难度和可操作性低的问题，因此一般不予考虑.同时，当第一排锚索距桩顶分别为1 m、1.5 m、2 m和2.5 m时，桩顶位移分别为16.39 mm、21.46 mm、30.08 mm和40.31 mm，即第一排锚索每下移0.5 m，位移增加约10 mm；由此可见，桩顶水平位移主要由第一排锚索的位置来控制，也说明了第一排锚索预应力大小对桩顶的位移约束有着决定性的作用.因此，对于变形要求严格的工程，可通过调整第一排锚索位置及其预应力大小来控制桩顶水平位移.

图6给出了坑顶地表最大沉降与锚索布置关系.当固定第一排锚索的位置，地表沉降值随着锚索间距的减小而减小，锚索间距每减少0.25 m时，沉降约减少2～4 mm，沉降-锚索位置关系线表现为一直线，四条直线基本平行；同时，地表沉降值随着第一排锚索的位置下移而增大，当第一排锚索距桩顶小于2 m时，锚索总体每上移0.25 m，沉降减少约5 mm，而当第一排锚索距桩顶大于2 m时，锚索总体每下移0.25 m，沉降增加约8 mm，增幅加大.

由上述分析可知，桩顶水平位移与坑顶沉降变化规律特征相似：第一排锚索位置较锚索间距对支护系统变形约束影响要大，尤其是桩顶水平位移，锚索间距对其影响甚微，造成这些特征是由于基坑支护系统变形通过第一排锚索预应力的施加而得到有效控制，因此，对于周边建筑物距离较近等对沉降要求严格的工程，应尽量将锚索的整体位置上移.一般场地各土层通常具有上软下硬特性，虽第一排锚索上调方案这种做法将会增长锚索长度，进而增加工程造价，但可以通过增大锚索安装倾角而得到有效缓解.

对于这种地质条件差的工程，控制基坑变形尤为重要，为达到该目的，本项目使锚索整体位置偏上(h=1.5 m)，适当增加锚索间距(d=2.5 m)，尽可能减少内力值，以达到经济合理.从本工程基坑开挖及运营整个过程来看，此方案可行，达到了预期的目标.

4 结论

本文以实际工程为依托，以桩身内力与基坑变形为考察指标，开展桩锚基坑支护锚索位置优化分析，以期为同类工程提供一定的参考与借鉴意义.通过分析，得到以下几点结论：

(1)索间距一定时，基坑第一排锚索位置越靠近桩顶，桩顶水平位移与坑顶沉降值越小，而桩身弯矩和剪力则越大；

(2)第一排锚索位置一定时，随着锚索间距的增加，桩身内力越小，而坑顶沉降则越大，桩顶水平位移则影响甚微；

(3)与锚索间距因素相比，第一排锚索位置对桩身内力和基坑变形的影响更为显著；

(4)桩身内力在一定范围内与第一排锚索位置和锚索间距两个参数成比例关系；随着第一排锚索远离桩顶，锚索间距的变化对内力值影响越来减小，甚至出现负影响的情况.在实际工程中，应避免将锚索总体位置设置偏下，且不宜将锚索间距调得过大；

(5)工程中，可通过调高第一排锚索位置以约束基坑变形，可适当加大锚索间距以减小桩身内力，以此达到基坑安全经济实用的目的.