用Phyphox测量双线摆周期及角振幅对双线摆周期的影响
胡耕硕
四川大学匹兹堡学院 四川 成都610000
实验背景
双线摆测量转动惯量是大学物理实验的创新内容。该实验通过测量双线摆的周期,代入公式解的转动惯量。因此,随着测量精度要求的提高,提高周期的测量精确度至关重要。
一般情况下,双线摆实验中角振幅应小于5°,对其具体值不做要求。如实验讲义所示[1]:

因此本实验选取角振幅为2°,4°下分别进行实验测量和数据分析,以研究角振幅对双线摆周期的影响。
1 角振幅对双线摆周期的影响
如讲义图所示为双线摆结构图[1]。
忽略细绳质量并将将摆件看成质点,采用等效摆长法,将其可视为单摆。
当摆角振幅θ很小是,双线摆周期为:

其中σ为考虑。角振幅大小后的修正项
2 实验内容
2.1 实验器材 由于新冠疫情影响只能居家实验,实验使用U型架,智能手机(装有Phyphox),吊线,物块,游标卡尺,量角器。
2.2 实验步骤 连接器材如图讲义[1],不断改变双线摆与u型架的夹角α,在角振幅分别为2°和4°的条件下进行多组实验,每个夹角α的情况下,用Phyphox对周期进行3次测量。
3 实验数据
当角振幅θ=2°,APP所测周期/s
α=81°第一次:0.60s第二次:0.62s第三次:0.59s平均值:
0.603s
α=83°第一次:0.70s第二次:0.71s第三次:0.69s平均值:
0.700s
α=90°第一次:1.36s第二次:1.35s第三次:1.36s平均值:
0.726s
α=107°第一次:0.74s第二次:0.73s第三次:0.71s平均值:0.726s
α=120°第一次:0.31s第二次:0.32s第三次:0.37s平均值:0.333s
当角振幅θ=4°,APP所测周期/s
α=81°第一次:1.30s第二次:1.31s第三次:1.33s平均值:1.310s
α=83°第一次:1.33s第二次:1.34s第三次:1.36s平均值:1.340s
α=90°第一次:1.34s第二次:1.35s第三次:1.35s平均值:1.350s
α=107°第一次:1.30s第二次:1.27s第三次:1.26s平均值:1.280s
α=120°第一次:1.29s第二次:1.26s第三次:1.25s平均值:1.270s
4 实验数据分析

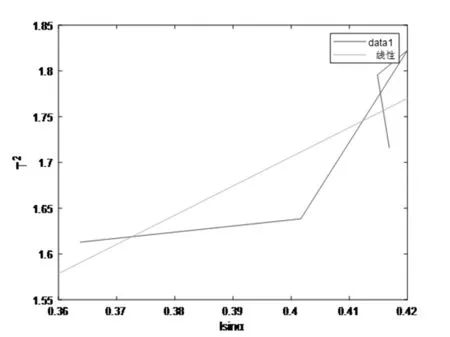
T2=3.1903sinα+0.43009
残差范数:0.11089
2.最小二乘法拟合
B与-3.1903相似
3.Excel算相关系数,相关系数为0.82。
4.系统误差:
当角振幅θ=2°通过比较,理论值与实际值相差过大,可能因为角振幅过小,导致智能手机传感器失效。故不宜使用角振幅θ=2°进行居家实验。
当角振幅θ=4°
α=81°,理论值:1.293,系统误差:0.017
α=83°,理论值:1.297,系统误差:0.043
α=90°,理论值:1.301,系统误差:0.049
α=107°,理论值:1.273,系统误差:0.007
α=120°,理论值:1.211,系统误差:0.059
系统误差较小,可用于居家实验
5.误差分析
(1)由于手机应用软件敏感度不足,导致再测量在θ=2°的情况下,所测周期与理论值相差巨大,应该改变应用软件灵敏度以进一步验证。
(2)所测过程中,存在人为导致误差,同时受器材准确性限制。
6.总结
在做居家实验用手机应用Phyphox,测量双线摆周期时,角振幅对实验结果有影响。实验结果表明,宜用角振幅为4°,线长为42c m,进行实验,会引起实验误差,进而造成系统误差。
因此在用双线摆测量物件转动惯量时应考虑角振幅对实验结果的影响以增加实验结果的准确性。但根据误差数据所示,该应用软件测量误差小,操作方便,可将该居家实验作为大学物理创新实验进行推广和普及。

