Kolmogorov型方程的多参数反演分析
赵 晶 晶
(兰州交通大学 数理学院,甘肃 兰州 730070)
偏微分方程[1]已经发展了几百年,其在物理学、工程技术以及其他许多领域都有广泛的应用。物理学和工程技术中出现的偏微分方程问题可以分为两大类:一类是正问题,其研究在理论和应用上都比较成熟;另一类是反问题[2],反问题起着由果寻因的作用,其研究目前还不是很成熟。其中,反问题的不适定性[3]是反问题研究的最大难点。在现实生活中存在大量的反问题,例如通过地震波的测量来判断地球内部的结构或地下矿藏的位置,利用红外线扫描来探测固体材料中的缺陷,利用X光分层扫描构像来作医学诊断,等等。 由于反问题在理论研究和现实生活中的重要性,近些年来有许多学者对反问题做了研究,尤其是对抛物型方程的反问题进行了大量研究。例如:抛物型方程的源项反演问题[4-5],抛物型方程的系数重构问题[6-7],Jiang等[8]研究了从期权的当前市场价格中重构Black-Scholes方程中隐含波动率的反问题,蔡超等[9]研究了在给定附加条件下Kolmogorov型方程系数b(x,t)的反演问题:
ut-Δu+b(x,t)ux=f(x,t),(x,t)∈QT=(0,l)×(0,T]。
Yamamoto等[10]首次研究了同时重构热传导方程的初始温度和辐射系数的反问题,并利用Tikhonov正则化方法得到了该问题的数值解。
本文研究了同时重构Kolmogorov型方程的初值和一阶项系数的反问题。此类问题在随机控制和金融数学中都有很重要的应用[11]。具体数学模型:
问题P记Q={(x,t)|0 (1) u(x,t)=z(x,t),(x,t)∈ω×(0,T), (2) u(x,T)=zT(x),x∈Ω。 (3) 这里ω=(a,b)⊂(0,l)=Ω,ω是Ω的任意子集。如何利用条件(1)- 条件(3)求解函数s(x)、φ(x)和u(x,t)。 假设可测量函数z(x,t)和zT(x)满足下列条件: z(x,t)∈L2(0,T;L2(ω)),zT(x)∈L2(Ω)。 (4) 由于问题P是不适定的,即它的解不连续、依赖于观测数据。我们转而考虑下面的最优控制问题: (5) 其中: (6) A1={s(x)||s(x)|≤M1,s∈H1(Ω)}, (7) A2={φ(x)|0<φ(x)≤M2,φ∈H1(Ω)}, (8) 这里M1和M2是两个给定的正常数,σ是一个比较小的正常数。对于给定的系数s(x)∈A1和初值φ(x)∈A2,函数u(x,t;s,φ)是方程(1)的解。α和β是正则化参数。 由抛物型方程的Schauder理论可知,对给定的系数s(x)和初值φ(x),方程(1)有唯一的解u(x,t)。以下是关于u(x,t)的一些估计。 引理1 设u(x,t)是问题(1)的解,则对u(x,t)有如下估计: (9) 本文中如果没有特别说明,将用C表示与T无关的不同情形下的常数。 引理2 令u(x,t)是问题(1)的解,则对s(x)∈A1、φ(x)∈A2有如下对u(x,t)的能量估计: (10) (11) (12) 定理1的证明与文献[8]中定理3.1的证明类似,此处不再赘述。 定理2 令(sn,φn)是控制问题(5)的解,则对任意的(h,k)∈A1×A2,有 (13) 其中,ξ(x,t)和η(x,t)满足 (14) (15) 最优控制问题P1是非凸的,人们并不期望得到它的唯一解。众所周知,对于没有唯一解的反问题,最优化方法是求解它的通解的一个经典的方法。然而,如果终端时间T比较小的话,那么惩罚泛函的最小值可以被证明是局部唯一且稳定的,这也是本文主要要去求证的部分。 假设{s1,φ1}是最优控制问题P1对应于{z1(x,t),z1(x,T)}的解,{s2,φ2}是最优控制问题P1对应于{z2(x,t),z2(x,T)}的解。 令 u1(x,t;s,φ)=u(x,t,s1,φ1), u2(x,t;s,φ)=u(x,t,s2,φ2)。 设 u1-u2=U, s1-s2=S, φ1-φ2=Φ。 则U满足 (16) 在式(13)中,当(s,φ)=(s1,φ1)时,取(h,k)=(s2,φ2);当(s,φ)=(s2,φ2)时,取(h,k)=(s1,φ1)。 于是有 (17) 且有 (18) 则由式(17)和式(18)可得 (19) 对于I1有 (u2-z2)(ξ2+η2)]dxdt ≡I11+I12+I13+I14。 (20) 同样地,对于I2有 ≡I21+I22+I23+I24。 (21) 其中ξ1、ξ2、η1和η2满足 (22) (23) (24) (25) 令 ξ1+ξ2=Ξ, 则Ξ、N和V满足 (26) (27) (28) 引理3 对于方程(16)有如下估计 (29) (30) 其中C与T无关。 引理4 对于方程(23)和方程(25),有如下估计成立: (31) (32) (33) (34) 其中C与T无关。 引理5 对Ξ、N和V,有如下估计式: (35) (36) (37) 定理3 令{s1,φ1}和{s2,φ2}分别是最优控制问题P1对应于{z1(x,t),z1(x,T)}和{z2(x,t),z2(x,T)}的最优解,如果有 s1|x=0=s2|x=0,s1|x=l=s2|x=l,φ1|x=0=φ2|x=0,φ1|x=l=φ2|x=l。 (38) 则存在一个常数T0,0 ‖s1-s2‖H1(Ω)+‖φ1-φ2‖H1(Ω)≤C(‖z1-z2‖L2(0,T;L2(ω))+‖z1(x,T)-z2(x,T)‖L2(Ω))。 (39) 其中C是与T无关的常数。 证明:由式(20)得,对于I1有 (40) 根据引理1和式(4),显然可以得到 (41) 其中C是与T无关的常数。 再根据引理3、引理5、式(40)和式(41)可推出 (42) 应用Soblev嵌入定理: max|S|≤C‖S‖L2(Ω)。 (43) 从而根据柯西不等式、式(40)、式(41)和引理2可得 (44) 同样地,对于I2可以得出 (45) 注意到条件(38),有下面的Poincaré不等式: ‖Φ‖H1(Ω)≤C‖Φ‖L2(Ω),‖S‖H1(Ω)≤C‖S‖L2(Ω)。 (46) 则结合式(19)、式(44)、式(45)和Poincaré不等式(46),有 (47) 其中C与T无关。 因此,对于固定的α和β,假设T0<<1,令 (48) 则对任意的0 (49) 最后,再次应用Poincaré不等式可以得到 (50) 其中C由正则化参数α和β决定,定理3得证。 本文主要从理论角度出发,使用最优控制理论来讨论问题P。在最优控制框架下,将问题P转化为一个最优控制问题P1,紧接着证明了最优化问题解的局部适定性(即解的存在性、唯一性与稳定性)。与通常的单参数控制问题不同,本文控制泛函含有两个未知参数和两个独立的正则化参数。该问题的主要难度在于各参数之间的相互影响,特别是二者所对应的反演不适定程度大不相同(系数反问题相对温和,而初值反演是强不适定),这也是本文的主要特色。我们的结果为将来的数值模拟打下了坚实的理论基础。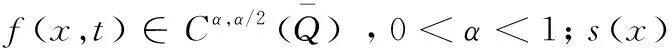
1 最优控制问题
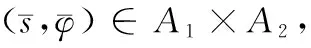
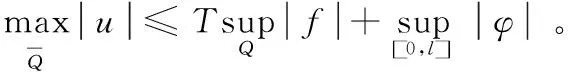
2 存在性
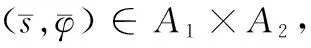
3 必要条件
4 局部唯一性与稳定性
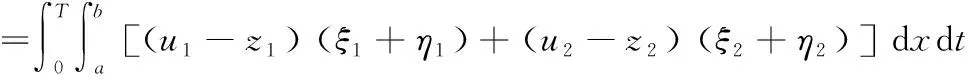
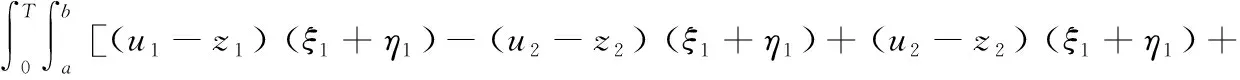
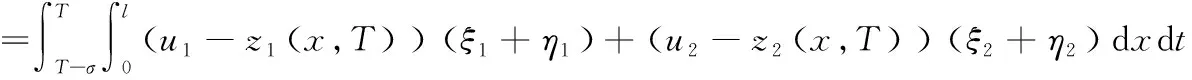
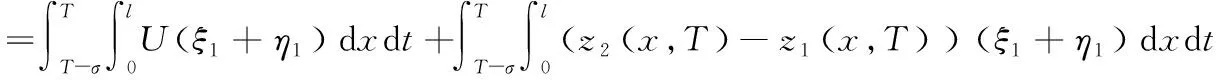
η1+η2=N,
ξ1+η1=V。
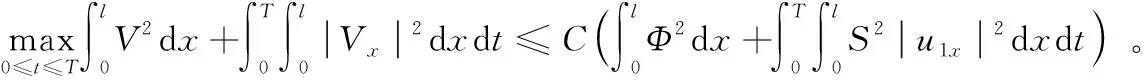
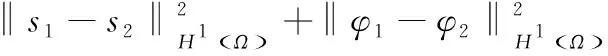
5 结 语

