基于最大熵模型预测东北地区红松潜在分布

张劳模，庞丽峰，许等平，唐小明

（1.中国林业科学研究院 资源信息研究所，北京 100091；2.河南工程学院 计算机学院，河南 郑州 450000；3.国家林业局林产工业规划设计院，北京 100010）

【研究意义】红松是我国重要的珍贵树种，同时也是国家储备林树种之一。红松最高可长到40多米，平均直径可超过1 m，有些甚至可以达到甚至超过2 m。一般来说，红松生长时间较长，至少可以存活500年。由于特殊的地理和气候条件，红松主要分布在中国的东北部，即小兴安岭和长白山附近[1]。近年来，由于气候变化和人类活动增加，红松的数量正在逐渐减少。因此，探究红松可能的分布范围和适宜区域，明确其余环境变量之间的定量关系，对于红松的保护具有重要的意义和实施必要。【前人研究进展】物种分布模型（SDMs）是基于一定算法和物种分布数据与环境因素的模型，可以以概率的形式计算物种或种群生态位，并显示适宜物种生存的生境范围[2]。物种由于受到环境因素的制约，其地理分布一般都相对稳定，在此前提下，物种分布模型（SDMs）假设物种和环境之间存在一些定量关系，物种只能在一定的环境范围内生存，低于或高于某个环境阈值，物种则无法生存[3]。目前，物种分布模型（SDMs）已成为生态学和生物地理学研究的重要工具，尤其是在全球变化背景下物种潜在分布研究领域[4-6]。典型的物种分布模型（SDMs）主要有 MaxEnt[7]、BIOCLIM[8]、PORSKA[9]、GAM[10]、GLM[11]、LANDIS[12]等，在这些模型之中，最大熵模型（maximum entropy model，MaxEnt）是最可靠的模型之一[13-15]。最大熵模型（MaxEnt）是一种基于最大熵理论，利用已知物种地理分布点和环境变量预测潜在分布的模型[16-18]，与其他模型相比，在数据有部分缺少或者样本容量很小的情况下，该模型的预测精度依旧稳定可靠。此外，该模型还可以计算物种适宜区域潜在分布图和环境因子重要性顺序[19]。2006年，Phillips[7]首先将MaxEnt模型应用于生态学研究中，随后越来越多利用MaxEnt模型研究物种潜在分布和适宜性评价的生态学研究成果相继发表。这些研究大多是利用温度和降水等环境因素预测物种的潜在分布，研究尺度一般为全球、全国或区域[20-24]。近年来对MaxEnt的研究开始关注于模型精度和不确定性分析，以及模型之间的对比[25-28]。

【本研究切入点】经过多年的应用，MaxEnt模型的参数已经比较固定，大部分研究者会使用默认的参数来做相关工作。最近的研究表明，当MaxEnt模型使用默认参数时，模型对采样偏倚敏感，容易产生过拟合现象[29]。作为一种新型简便的物种分布预测机器学习方法，研究MaxEnt模型的不确定性是十分必要的。在MaxEnt模型的所有参数中，随机测试百分数是最重要的参数之一，这是计算模型AUC值的重要参数。在MaxEnt模型中，默认利用75%的现有数据作为训练数据，25%作为测试数据，而此数值是否合理需要进行进一步的研究和讨论。【拟解决的关键问题】为了探究MaxEnt模型不同参数设置对于精度的影响，以及了解环境因素对于红松分布的影响，本研究计算了不同训练和测试数据比例条件下的AUC，评估环境变量的相对重要性，利用红松分布点和环境数据，结合MaxEnt模型预测了红松的潜在分布，分析环境因子对红松的不同影响程度。

1 材料和方法

1.1 研究区概况

中国东北地区（118°53′～135°05′E，38°43′～53°35′N），包括黑龙江省、吉林省和辽宁省，总面积约787 300 km2（图1）。该地区纬度较高，因此冬季漫长而寒冷，夏季短暂而温暖。该地区的年平均温度在5～10℃，年均降水量为400～1 000 mm，年平均气温由北向南逐渐升高，年均降水量空间分布不均匀，从西到东、从北到南呈上升趋势。特殊的气候和土壤条件使得东北地区森林面积广袤，是我国主要的林区之一。广大的山区森林资源丰富，约占中国森林总量的三分之一。除红松外，该地区也生长着蒙古栎、水曲柳、樟子松等珍稀树种。

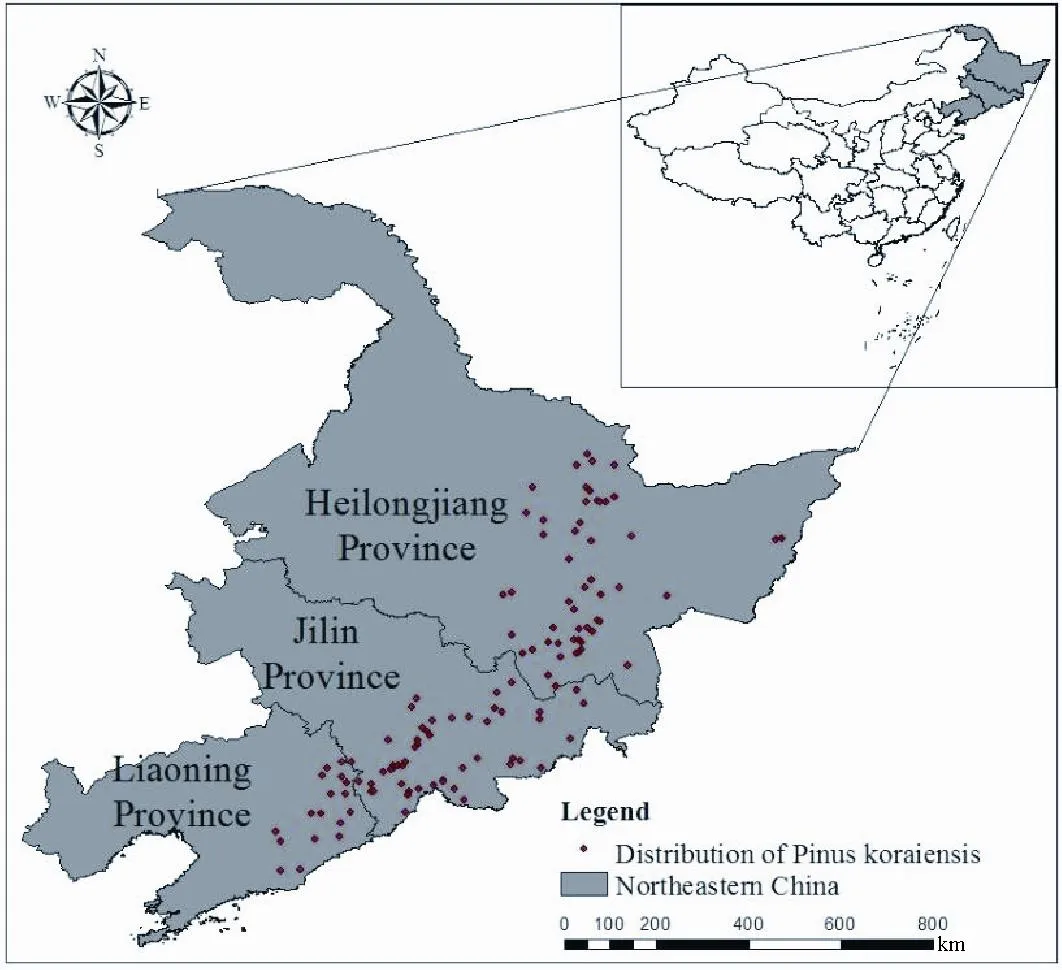
图1 中国东北地区的地理位置和红松分布点Fig.1 The Location of Northeastern China and the Distribution of Pinus koraiensis

1.2 数据来源

在国家森林资源连续清查数据中收集了东北地区159个红松分布点。国家森林资源连续清查，也叫做一类调查，是一种森林资源调查方法，旨在监测我国森林资源的状况和动态变化，采用固定地点进行定期重复调查，是国家森林资源综合监测系统的重要组成部分。

环境数据来源于世界气象http://www.worldclim.org，其中包括了19个环境变量，如表1所示。这些数据是根据世界各地气象站1950年到2000年的观测数据，通过空间插值实现的栅格数据集，被广泛用于生态系统的相关研究中。

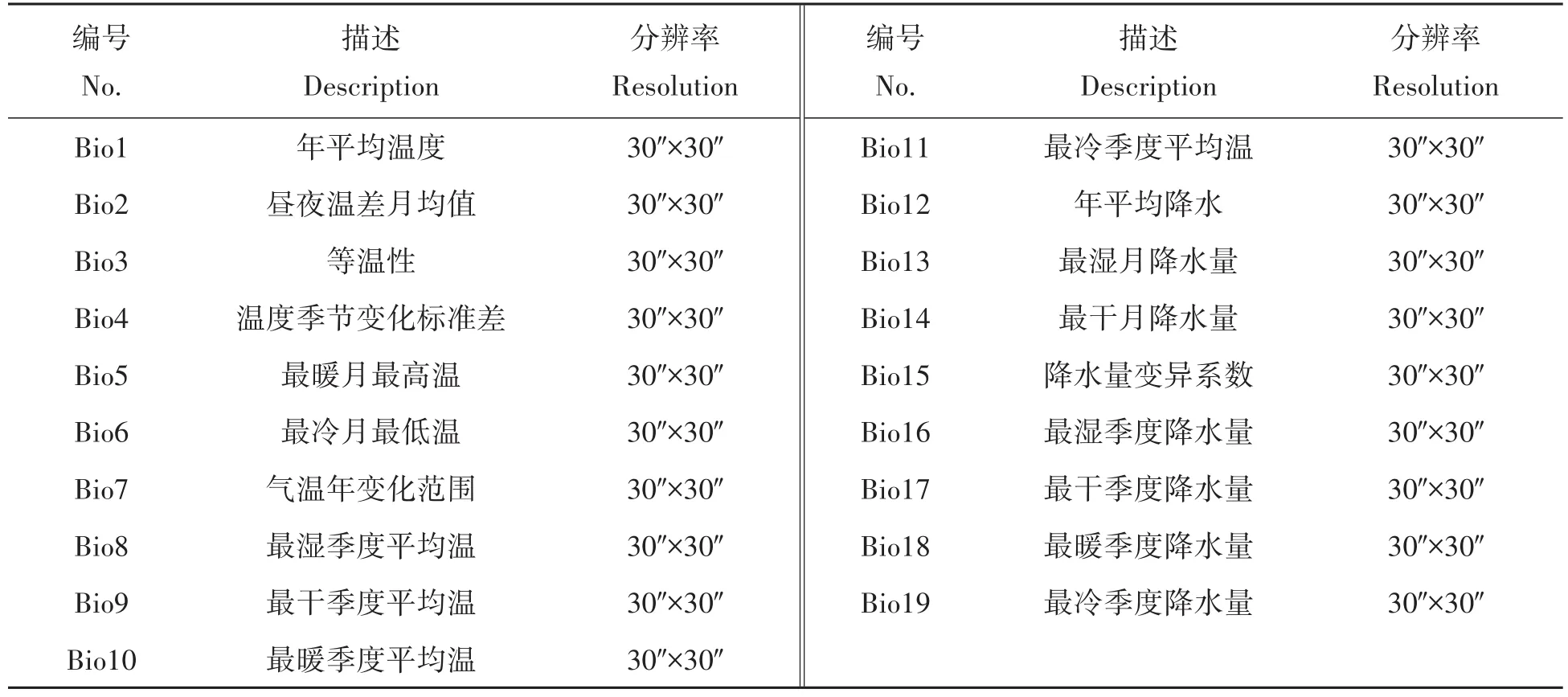
表1 模型红松潜在分布的生物气候因子Tab.1 Environmental variables used for modeling the potential distribution of Pinus koraiensis

1.3 最大熵（MaxEnt）模型

MaxEnt模型是基于最大熵原理构建的模型，利用熵来度量随机变量的不确定性，即不确定性随熵的增加而增加。一般在没有外界影响的情况下，熵会随着随机变量的增加而增加。1957年，Jaynes[30]提出了最大熵理论（MAXENT），该理论认为在外部条件准备充分和没有任何主观的假设的情况下可以接近一个随机事件真实状态的概率分布，因为只有当这个概率分布最均匀和熵最大时，误差是最低的。Philips首次将最大熵模型应用于物种分布研究中，在确定特征空间的前提下，计算限制物种分布的约束条件，建立约束条件与特征空间的关系，利用MaxEnt模型从区域中选择最优分布范围。

物种分布点数据和环境变量数据是构建Maxent模型的基础数据。物种分布点使用经度和纬度表示，环境变量主要包括气候、植被覆盖和地貌等。MaxEnt利用物种分布点的环境变量数据建立预测模型，并将该模型用于模拟区域物种可能的分布范围[13，16]。

模型预测能力的判断指标是ROC曲线（receive operating characteristic curve），ROC曲线由纵坐标的特异性和横坐标的敏感性构成。ROC曲线与横坐标之间的面积为曲线下面积AUC（area under curve），可以用来衡量模型的整体性能，评估模型的准确性。AUC值通常在0.5～l（表2），AUC值越接近1，预测精度越高，预测结果越准确。利用折叠法可以判断每个环境变量的重要性，有助于选择影响物种分布的主导环境因素。

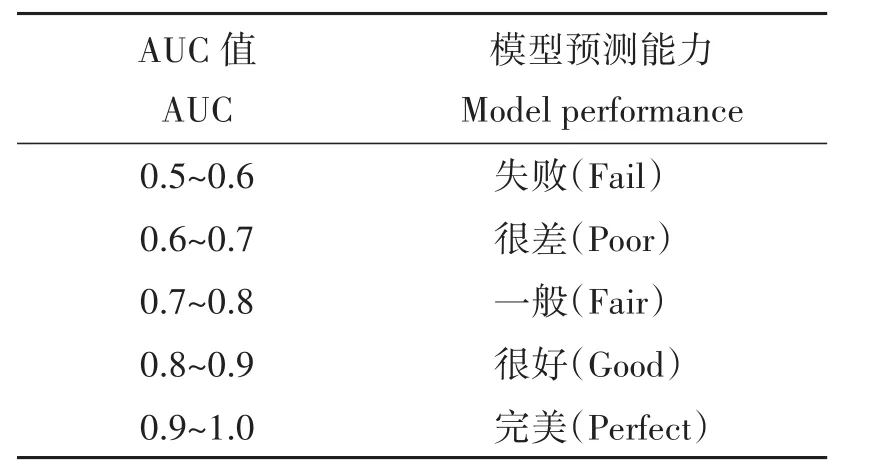
表2 模型精度评价标准Tab.2 Evaluation criteria of model accuracy

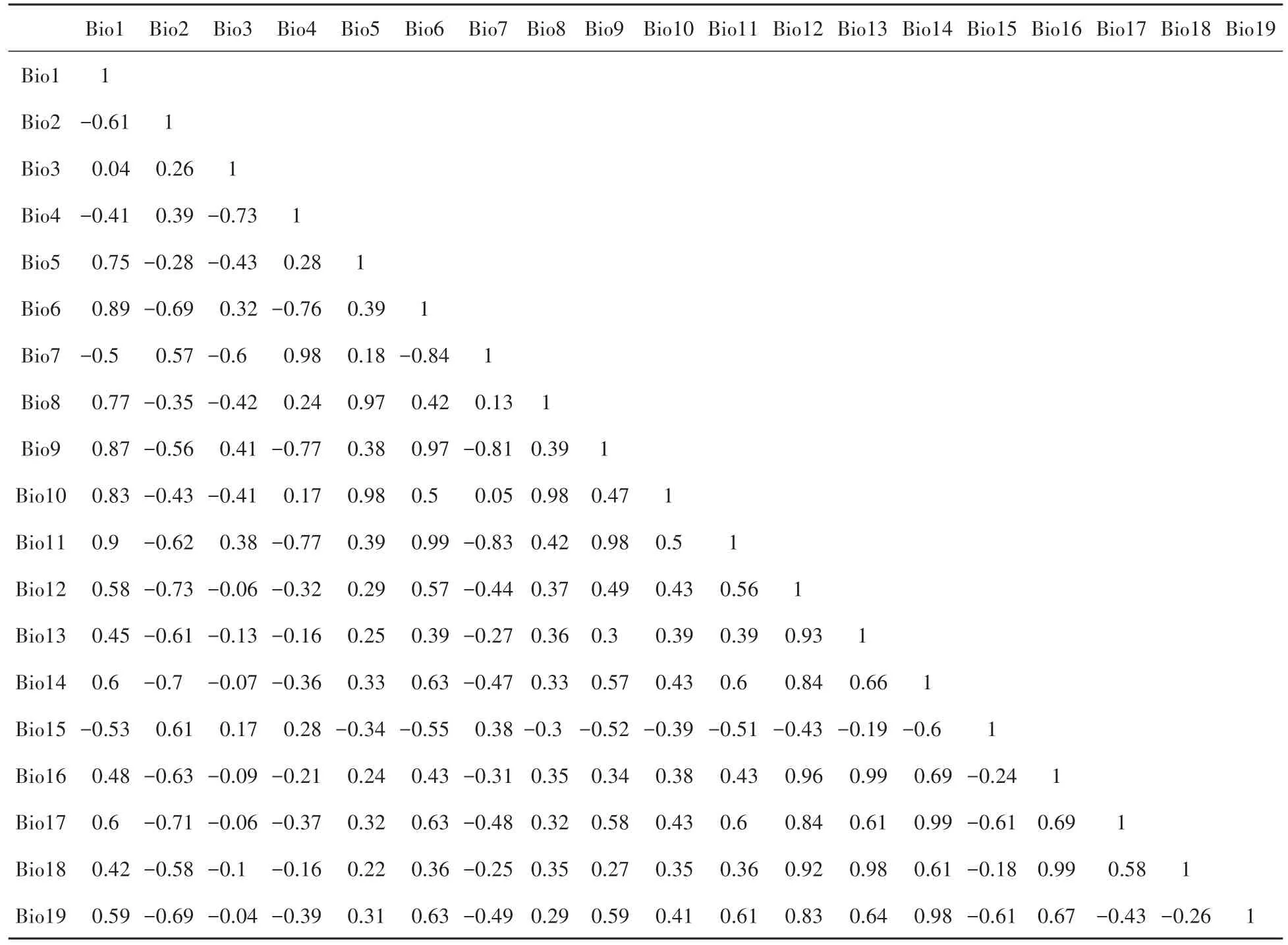
表3 环境因子相关性矩阵Tab.3 The correlation coefficient matrix of environment variables

1.4 环境变量筛选

数据的相关性会影响模型的准确性和预测结果。一般来说，变量之间相对独立是统计建模的前提，所以需要进行数据的筛选，使得数据之间的相关性最小，但是所保留的数据又有一定的代表性。本研究中通过相关系数选取变量。不同环境变量之间的相关系数如表3所示，如果两个变量因子之间的系数大于0.9，则将其中一个剔除。选择后，环境变量的数量减少了一半，筛选前后数据情况如表4所示。

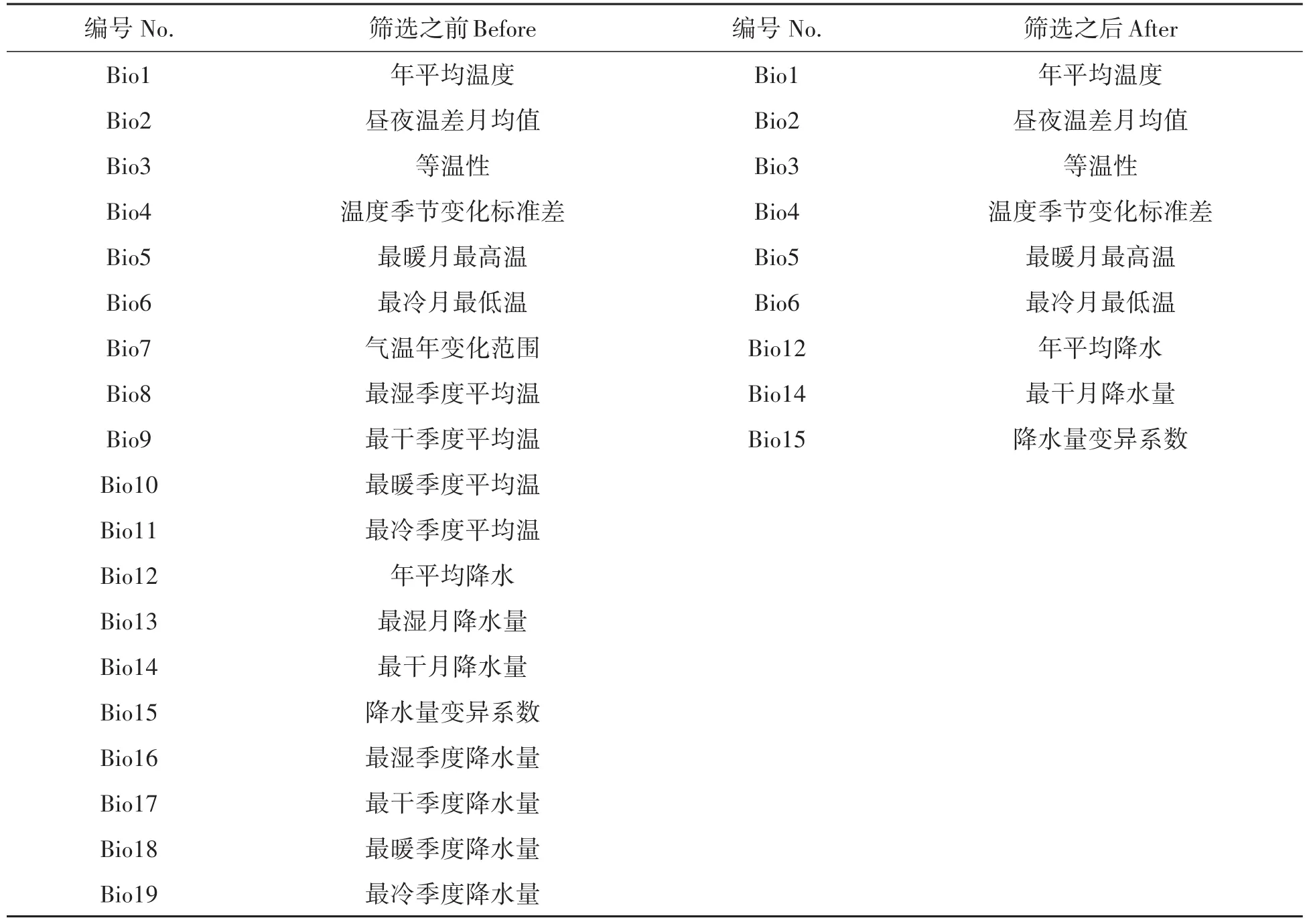
表4 数据筛选结果Tab.4 Factor selection results

1.5 测试数据集的百分比

本研究将间隔设置为10%，即测试比例分别为5%、15%、25%、35%、45%和55%，训练集分别为95%、85%、75%、65%、55%和45%。25%是模型的默认值。同时还对测试数据和训练数据设置了50%的比例，计算在等量比例的情况下精度结果。

2 结果与结论

2.1 模型精度分析

不同随机测试百分比的AUC比较结果如图2和表4所示。训练数据的AUC在不同百分比下的范围为0.890～0.898，而测试数据的AUC在不同百分比下的范围为0.854～0.884。整体上来看，各百分比精度相对较高，模型精度合理。然而，两个数据集的精度变化趋势却是相反的。对于训练数据，在15%之后，模型精度逐渐上升，但是对于测试数据，精度却在下降。

同样值得注意的是，测试数据的变化速度明显高于训练数据。在相同的百分比变化范围内（15%～45%），训练数据的AUC仅增加了0.08，而测试数据却减少了0.3。此外，15%和45%是两个极值百分比，在15%时，训练数据的准确率最低，而测试数据的准确率最高。在45%时，测试数据的准确率最低，而训练数据的准确率最高。显然，很难找到训练数据和测试数据都具有良好准确率的最优百分比，相对而言，当百分比为5%时，两组数据的准确率都比较准确。

图2 不同随机测试百分比下的精度对比Fig.2 Accuracy comparison of different random test percentage

表5 不同随机测试百分比下的模型精度Tab.5 The accuracy of model under different random test percentage

图3 不同比例下环境变量对红松生境影响的折叠法测试结果Fig.3 The results of the jackknife test of variables’contribution in modelling Pinus koraiensis’s habitat distribution

2.2 变量的重要性

不同随机检验百分比中，环境因子贡献度的折叠法测试结果如图3所示，不同随机测试百分比下排名前三的环境因子见表5。从结果可以看出，无论在任何比例的百分比中，Bio12（年平均降水），Bio14（最干月降水量）和Bio15（降水量变异系数）都稳定排名前3，这些环境变量都与降水有关。这些变量的排序在不同的随机测试百分比中有所不同，随着百分比的增加，Bio12和Bio15号交替占据了第一的位置，但是在百分比为55%时，第二名则被Bio14取代。

表6 不同随机测试百分比下排名前三的环境因子Tab.6 The top three environmental factors of different random test percentage

2.3 红松潜在分布模拟

图4为利用MaxEnt模型模拟的东北红松的潜在分布结果，使用的随机测试百分比为5%。从图中可以看出，红松的主要潜在分布范围在东北和西南地区，特别是在辽宁省和吉林省的交界处。而在吉林省和黑龙江省交界处的东部，也有一片面积相对较大的分布区域。同时，在黑龙江省的中北部地区，也存在部分潜在分布区域。

图4 红松潜在分布模拟结果Fig.4 Predicted potential distribution of Pinus koraiensis

3 结论与讨论

最大熵MaxEnt模型使用与已知物种分布点相关的环境变量来模拟物种分布，模型在模拟分布时，通过数据构建物种的分布模型，然后将其转移到另一个地理区域模拟潜在分布。本研究基于MaxEnt模型和环境变量模拟了红松的分布，计算了不同训练和测试数据比例条件下的AUC，然后评估了环境变量的相对重要性。

3.1 随机测试百分比对模型精度的影响

MaxEnt默认参数的设置来源于数据的测试结果，早期模型开发人员使用来自6个不同地理区域的266种物种的数据获得了这些参数，他们利用大量的物种分布数据和各种实验方案，以得到最优的模型参数作为默认参数，以促进和简化模型。经过多年的发展，这些参数逐渐被广泛接受。然而，当转移到不同的地理空间模拟物种的潜在分布时，原模型的默认参数可能不再适用。随机测试百分比是模型中最重要的参数之一。本研究结果证明25%不是精度最高的数值，最适比例为5%。所以当使用默认值时，精度并不是最高的，这将在一定程度上影响模型结果。

3.2 红松分布与环境变量

在2.2中，本研究计算影响红松分布最重要的环境因子是降水，但是前人的研究表明，植物的分布主要受温度的影响[19，31-32]。这与本研究结果完全不同，但是这并不意味着温度对红松的分布没有影响。事实上，这一地区的温度差异较小，因此大部分地区的温度都可以满足红松的生长。但是降水却存在明显的空间差异。

东北地区年降水量和年平均气温如图5所示，从图中可以明显看出，东北地区的极端低温主要发生在西北地区，而其他地区的平均年温差较小且相对温暖。因此，从温度的角度来看，能够满足红松生长温度范围的地区很宽，所以在该地区，温度不足以限制红松的分布，或者说已经满足了红松生长的要求，在这种情况下，降水的作用反而得以凸显。从图中可以看出，年降水量的空间分布呈现由西向东、由北向南的递增趋势。年降水量较多的地区与红松的潜在分布地区有着较高的匹配程度，年降水量较少的地区，如东北西部，红松潜在分布范围也相对较少。

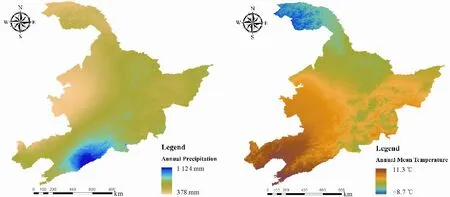
图5 东北地区年降水和年均气温分布Fig.5 Annual precipitation and annual mean temperature in Northeastern China

3.3 红松的潜在分布

本研究通过红松分布点和环境数据模拟了红松在东北地区的潜在分布范围，本研究提出的方法可用于模拟其他地区其他物种的潜在分布。同时，虽然物种在多数情况下会受到温度的影响，但是在东北地区，由于温度的空间差异较小，实际上影响植物分布的最重要因素是降水。另外，物种的分布还可能与地理复杂性或种间竞争，甚至人类的干扰有关，本文仅考虑了温度和降水对红松适应性分布的影响，未考虑土壤条件和地形因素等，这是下一步工作的重点。