面向大规模数据的特征趋势推理算法
吴 春 琼
(厦门大学 信息科学与技术学院, 福建 厦门 361005; 阳光学院 商学院, 福州 350015)
随着大规模数据信息时代的到来, 海量的数据都保存在网络和云存储中, 导致网络和云存储中的大规模数据数量与规模急剧增加, 因此在使用和调度大规模数据时, 必须对数据库与云存储系统中的大规模数据进行处理, 如特征提取和特征趋势推理等. 面向数据的特征趋势推理已成为目前该领域的关注热点. 文献[1]提出了一种随机变分推理算法, 但该算法未能在推理数据特征趋势前聚类大规模数据, 导致推理结果的误差较大; 文献[2]提出了一种并行化Top-kSkyline查询算法, 但该算法计算过程较复杂, 且效率较低; 文献[3]提出了一种基于直觉模糊Petri网的模糊推理算法, 但该算法未能推理数据的特征趋势, 不适用于处理推理的问题. 针对上述算法存在的问题, 本文提出一种新的面向大规模数据的特征趋势推理算法, 首先对大规模数据进行聚类, 获取最佳聚类结果后提取聚类结果的动态特征, 然后采用基于特征趋势规则的推理算法, 实现大规模数据的特征趋势推理.
1 算法设计
1.1 面向大规模数据聚类优化算法
本文使用Hash函数抽取样本体现数据的分布状况, 采用Pam算法和并行K-means聚类算法聚类样本数据, 将实际样本点设为新聚类中心, 防止受噪声点与孤立点的干扰, 以此提升聚类效果和速度[4], 获取最佳大规模数据聚类结果.
1.1.1 基于Hash函数的样本抽样 抽样Hash函数时, 必须计算大规模数据抽样样本的内存[5]. 将置信度取值为1-β, 由中心极限定理可知, 在正态整体里, 随机抽取m个样本, 大规模数据样本均值与正态分布相符[6]; 在偏态整体里抽样, 若m接近无穷大, 则大规模数据抽样分布与正态分布a~N(η,λ2)相符, 其中:η表示样本均值;λ2表示样本方差. 因此置信度是1-β的置信区间为

其中:a表示二元变量;β表示置信因子;Y表示置信匹配度. 假设抽样误差为γ, 则置信区间为[(1-γ)η,(1+γ)η]. 综合上述方法获取的大规模数据抽样样本数目m为
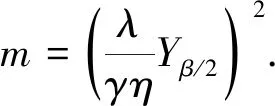
(1)
近似分布估计大规模数据各维变量时, 能建立如下Hash函数:
T(x1,x2,…,xm)=B(x1),B(x2),…,B(xm),
(2)
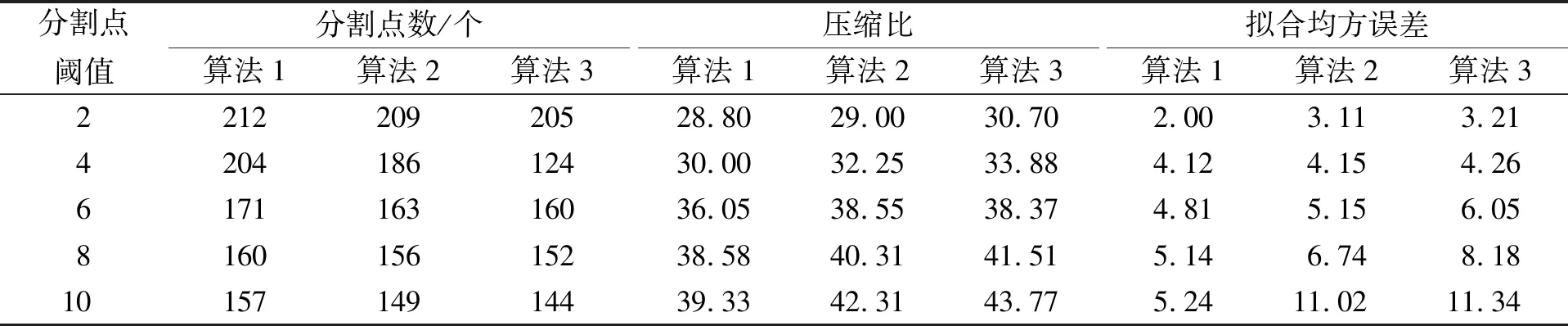
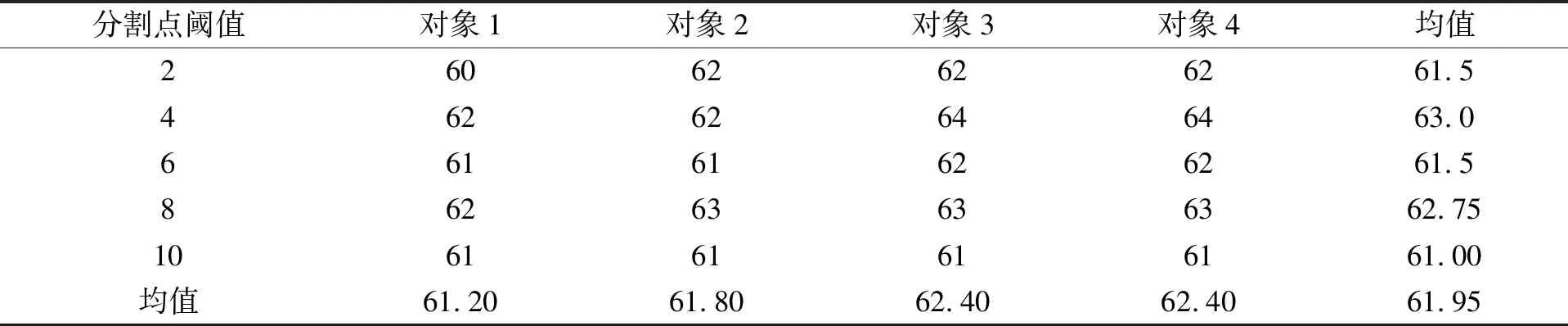
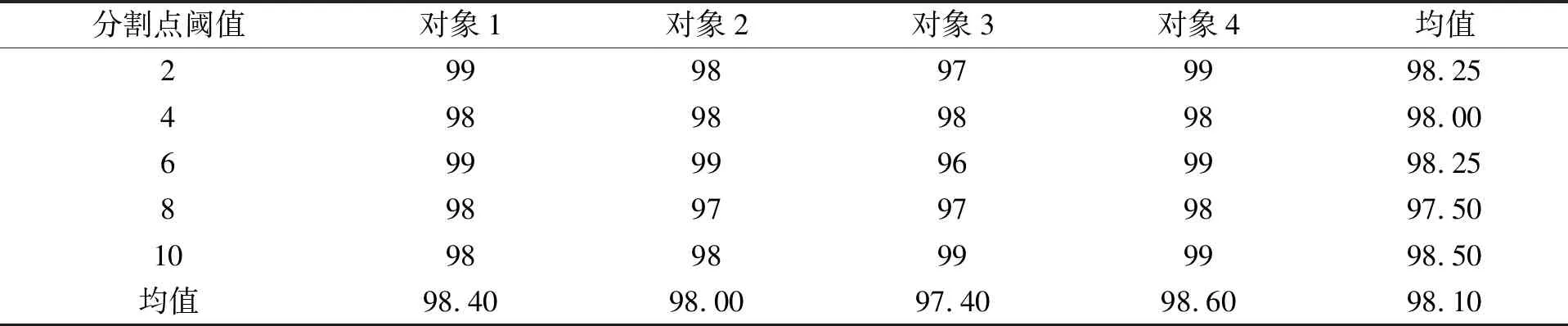
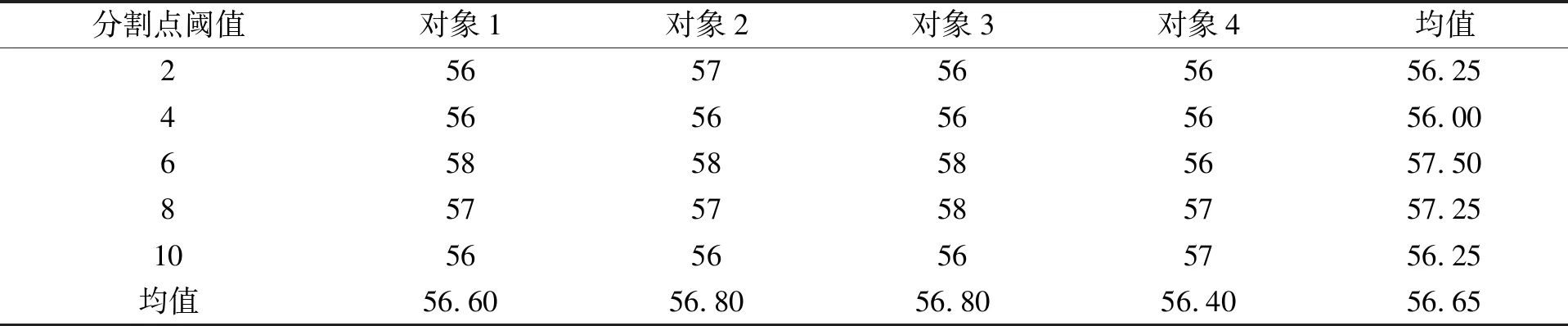
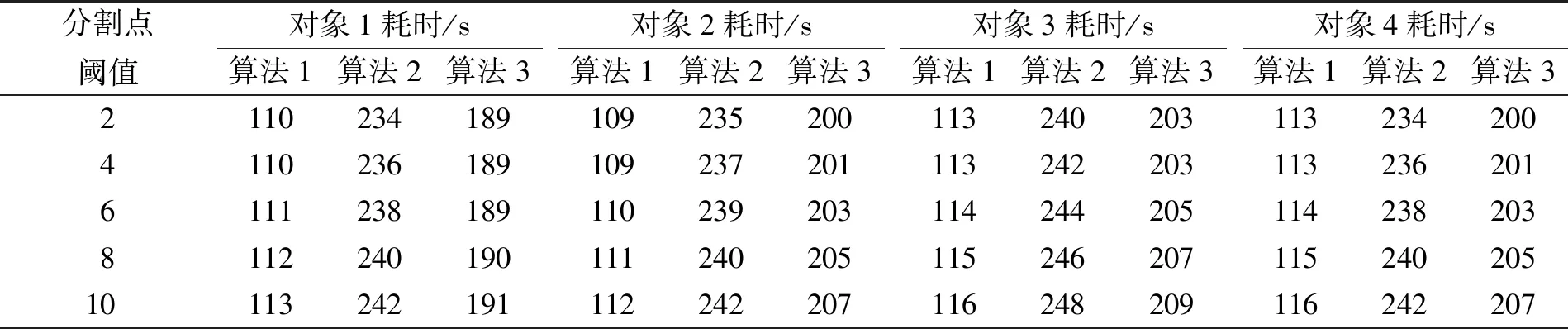
其中:B(x)表示分布函数;T(x)表示Hash函数;x表示分配目标. 设该Hash函数的值域为[0,1], 假设需要提取m个大规模数据的样本数据, 则把次区间m等分: 0=i1 ik-1 则将该目标分配至第k个桶内. 基于Hash函数的样本抽样算法流程如下: 步骤1) 设定大规模数据抽样样本内存m; 步骤2) 计算每列分布函数B(x); 步骤3) 建立Hash函数; 步骤4) 将全部大规模数据目标分配至m个桶内; 步骤5) 任意在各Hash桶内提取固定比例的大规模数据, 构建成m个样本数的大规模数据样本数据集[7]. 1.1.2 改进算法 改进算法步骤如下: 1) 计算大规模数据目标的均值和标准差[8]; 2) 设定大规模数据抽样的样本数目m; 3) 在数据集X中实行样本抽样; 4) 获取的抽样样本使用Pam聚类算法实行聚类, 最后提取初始中心[9]; 5) 将稳定的聚类中心设成全局初始聚类中心, 输入数据组和有关参数; 6) 使用并行K-means聚类算法再次聚类, 直至全部类簇稳定或运行至最大迭代次数时停止[10]. 大规模数据整体聚类流程如图1所示. 图1 聚类算法流程 通过上述过程获取最佳大规模数据聚类结果后, 提取大规模数据聚类的动态特征, 在此基础上采用基于特征趋势规则的推理算法, 实现大规模数据特征趋势的准确推理[11]. 本文设计的提取大规模数据各方面特征如下: 1) 压缩比数S为 2) 上升斜率均值L为 (3) 其中:Li表示斜率为正数的大规模数据段斜率;i=1,2,…,k,i和k表示计量参数;w表示极值点数; 3) 下降斜率均值J为 (4) 其中,Ji表示斜率为负数的大规模数据段斜率; 4) 分析极值点数w, 如果分割点前后数据段斜率符合不同且为反向关系, 则该分割点是极值点; 5) 大规模数据流均值R为 (5) 6) 大规模数据流的均方差χ为 (6) 其中:R表示大规模数据流均值;G表示大规模数据流数据量. 1.3.1 大规模数据特征的趋势规则推理模型 假设大规模数据聚类库C中字段d是趋势变化的轴,dmax和dmin描述d字段值的上下限,F表示d字段取值的间隔, 则将数据库C根据d字段取值分为C={C1,C2,…,Cn}, 大规模数据聚类库中相同特征种类Fj(j=1,2,…)在C1,C2,…,Cn内的记录数是{C1,C2,…,Cn}, 则{C1,C2,…,Cn}表示基于特征种类Fj的累计趋势规则. 如果采用相同特征种类Fj在C1,C2,…,Cn中的字段数据项之和是{H1,H2,…,Hn}, 则{H1,H2,…,Hn}表示基于特征种类Fj的合计趋势规则[12]. 累计趋势规则和合计趋势规则的不同是前者计算记录数, 后者计算合计数, 所以两种算法基本相同, 本文通过累计趋势规则方法设计趋势规则算法. 1.3.2 面向大规模数据特征趋势规则推理算法设计 面向大规模数据的特征趋势规则推理必须设定大规模数据特征趋势轴的初值、 终值和变化步长. 假设大规模数据特征趋势轴的字段为d, 初值是dmin, 终值是dmax, 变化步长为F, 则根据特征趋势轴的分类, 能将C划分为n个字库{C1,C2,…,Cn}, 假设B与C是等价关系,C共含有n个等价划分, 能获取下述矩阵,P1,j表示记录数. 矩阵的各列向量(P1,j,P2,j,…,Pn,j)(j=1,2,…,n)表示大规模数据特征趋势规则, 若可获取C上的全部等价关系, 便可获取所有大规模数据特征趋势规则[13]. 面向大规模数据特征趋势规则推理算法流程如下: Fori=dminTodmaxorderFdry Put intoCiinCWherei≤d≤i+F Next whole等价划分B={B1,B2,…,Bn} dry Fori=1 tondry Forj=1 tondry Choose count(*)intoR[i,j] inCj WhereBi等价类 Next Next R[i,j] ⟹ 结果库 Next. 本文实验设推理目标为铝电解槽电压数据, 其属于平稳大规模数据流, 有效推理铝电解槽电压的数据特征趋势能对槽况恶化情形进行提前预警[14]. 实验依次使用本文算法(算法1)、 随机变分推理算法(算法2)和并行化Top-kSkyline查询算法(算法3)对相同数据流特征进行趋势推理, 并用差异分割点阈值依次检验每个算法的性能指标: 1) 分割点点数设为ϖ1; 2) 压缩比S为 (7) 3) 拟合均方误差UMs为 (8) 其中:l表示大规模数据段的长度, 也是电压采样点的点数;q表示该数据段的拟合参数值;si表示实际电压;x1表示时间. 结合铝电解状况, 实验将基准窗口长度设为len=Z/4, 其中Z表示电压曲线波形周期, 该周期根据运行的工况设定, 初始值是110 min. 最长数据窗口长度是Zk,k是可变参数, 通常取值为1.5~2, 初始值为1.5. 标准分割点阈值用φ描述. 拟合均方误差主要用于判定算法推理结果的误差均值, 可分析数据特征趋势的变化水平, 实验在具有差异性的分割点检测阈值下, 对比上述3种算法的分割点点数、 压缩比和拟合均方误差, 对比结果列于表1. 由表1可见: 在相同阈值的前提下, 本文算法的最大分割点点数为212个, 分别比随机变分推理算法和并行化Top-kSkyline查询算法的最大分割点点数高3和7, 且本文算法的分割点点数始终大于其他两种算法, 说明本文算法在推理大规模数据的特征趋势时, 能全面分割大规模数据特征, 确保了大规模数据特征趋势推理结果的准确度; 压缩比数是数据流的数据量与分割总数间的比值, 表示实验所用大规模数据与分割总数成正比, 压缩比越小说明大规模数据特征分割的越全面, 本文算法、 并行化Top-kSkyline查询算法以及随机变分推理算法的最大压缩比排序为39.33<41.51<42.31, 且本文算法的压缩比始终小于另外两种算法, 说明本文算法分割的大规模数据特征更全面, 同样为大规模数据特征的准确推理提供了可靠依据; 从拟合均方误差方面分析, 本文算法的拟合均方误差最大值为5.24, 随机变分推理算法的拟合均方误差最大值为11.02, 并行化Top-kSkyline查询算法的拟合均方误差最大值为11.34, 本文算法的拟合均方误差最小, 说明本文算法平均误差最小, 分割大规模数据特征的准确率最高[15]. 表1 3种算法的数据分割点数、 压缩比、 拟合均方误差对比结果 基于上述实验设置, 设定4个大规模数据流特征推理对象, 统计3种算法的大规模数据特征趋势的推理准确率, 结果分别列于表2~表4. 由表2~表4可见, 随机变分推理算法对大规模数据特征趋势推理的准确率均值为61.95%, 本文算法对大规模数据特征趋势推理的准确率均值为98.10%, 并行化Top-kSkyline查询算法推理准确率均值为56.65%, 因此, 本文算法的推理准确率最高. 表2 随机变分推理算法的推理准确率(%) 表3 本文算法的推理准确率(%) 表4 并行化Top-k Skyline查询算法的推理准确率(%) 图2 3种算法的推理速度增长率对比结果 实验统计上述实验过程中3种算法的推理效率, 获取3种算法的推理速度增长率如图2所示. 由图2可见, 本文算法在大规模数据特征分割点阈值为1时, 推理大规模数据特征趋势的速度便出现增长趋势, 当大规模数据特征分割点阈值为10时, 本文算法的推理速度增长率高达50%; 随机变分推理算法在分割点阈值为4时推理速度才出现增长趋势, 当大规模数据特征分割点阈值为6~8时, 推理速度增长率达到顶峰, 速度增长率为30%, 当大规模数据特征分割点阈值大于8时速度增长率趋势回落; 并行化Top-kSkyline查询算法在分割点阈值为3时推理速度才出现增长趋势, 当分割点阈值为8时, 推理速度增长率最高为30%. 因此, 相对于其他两种算法, 本文算法的推理速度增长率最快, 是一种高效率的大规模数据特征趋势推理算法. 上述实验中3种算法的推理耗时对比结果列于表5. 由表5可见, 在不同分割点阈值下, 推理4个大规模数据的特征趋势时, 本文算法的推理耗时最大均值为114.25 s; 随机变分推理算法和并行化Top-kSkyline查询算法的推理耗时最大均值分别为243.5 s和203.5 s. 因此, 相对于其他两种算法, 本文算法的推理耗时最短, 效率最高. 表5 3种算法的推理耗时对比结果 综上所述, 本文提出了一种新的面向大规模数据的特征趋势推理算法, 使用Hash函数抽取样本体现数据的分布状况, 采用Pam算法和并行K-means聚类算法对大规模数据样本实行聚类, 将实际样本点设为新聚类中心, 防止受噪声点与孤立点的干扰, 以此提升聚类效果和速度; 获取最佳大规模数据聚类结果后提取大规模数据聚类的动态特征, 在此基础上采用基于特征趋势规则的推理算法, 实现大规模数据特征趋势的准确推理. 实验结果表明, 本文算法在推理大规模数据的特征趋势时, 推理的准确率均值为98.10%, 表明本文算法具有较高的准确率; 本文算法的推理速度增长率为50%, 推理耗时最大均值为114.25 s, 远低于随机变分推理算法和并行化Top-kSkyline查询算法的推理耗时, 说明本文算法的推理效率较高.
1.2 提取大规模数据聚类的动态特征
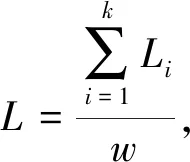
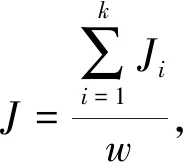
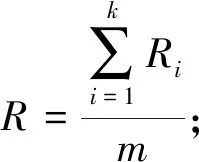

1.3 基于特征趋势规则的推理算法
2 实 验
2.1 实验设置

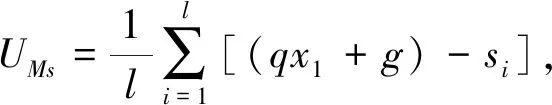
2.2 实验结果