混沌系统的广义修正函数投影同步及其电路仿真

李 德 奎

(甘肃中医药大学 理科教学部, 甘肃 定西 743000)

Pecora等[1]通过研究混沌运动实现了混沌同步, 混沌同步的实现为混沌在保密通信、 生态系统、 非线性系统性能最优化、 人工神经网络、 模式识别和系统辨识等领域的应用奠定了基础[2]. 目前, 关于混沌同步方式的研究已有很多成果, 如完全同步[3-4]、 反同步[5]、 广义同步[6]、 投影同步[7]、 函数投影同步[8]及修正函数投影同步[9]等. 修正函数投影同步是指驱动系统和响应系统的不同状态变量之间以不同的比例函数实现同步, 即同步误差定义为ei=yi-αi(t)xi(αi(t)是不全相同的函数). 易见完全同步、 反同步、 广义同步、 投影同步及函数投影同步均为修正函数投影同步的特殊情形.

近年来, 混沌系统的动力学分析及其电路仿真已引起人们广泛关注, 如文献[10-11]研究了混沌系统的稳定性和分岔行为分析, 并对混沌吸引子进行了电路仿真； 文献[12]研究了一个三维自治系统的分岔问题, 并设计了混沌吸引子的仿真电路； 文献[13]电路仿真了一个新四维超混沌系统的吸引子相图； 文献[14]设计了五维混沌Chen系统的仿真电路, 并得到了与数值仿真完全一致的混沌吸引子； 文献[15]利用线性分段函数, 构造了多翼混沌系统, 并设计了吸引子相图的仿真电路； 文献[16]设计了分数阶混沌系统的仿真电路. 但对混沌同步电路设计的研究目前文献报道较少, 其中混沌系统的广义修正函数投影同步的电路实现目前尚未见文献报道. 为进一步提高保密通信的信息安全级别, 在上述各种同步方式研究的基础上, 本文给出混沌系统的另一类同步方式----广义修正函数投影同步, 并设计其仿真电路.

1 广义修正函数投影同步定义

以任意连续的非线性混沌系统为驱动系统, 其动力学方程为

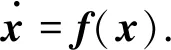
(1)

假设单向耦合的响应系统为

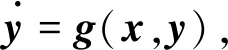
(2)

其中:x,y∈n分别为驱动系统和响应系统的状态变量；f(x),g(x,y)∈n分别为驱动系统和响应系统的非线性函数.

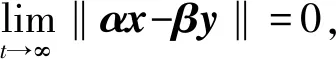
e=αx-βy,

(3)

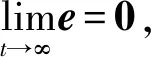
当α=I且β=I时(I为单位矩阵), 称为完全同步; 当α=I且β=-I时, 称为反同步; 当α=I且β为任意常对角矩阵时, 称为修正投影同步； 当α=I,β1(t),β2(t),…,βn(t)全相等时, 称为函数投影同步; 当α=I,β1(t),β2(t),…,βn(t)不全相等时, 称为修正函数投影同步. 因此, 广义修正函数投影同步是其他同步方式的更一般情形, 其他同步方式是广义修正函数投影同步的特殊情形.

2 广义修正函数投影同步的实现

基于驱动系统(1)和混沌系统的单向耦合原理, 构造相应的响应系统为

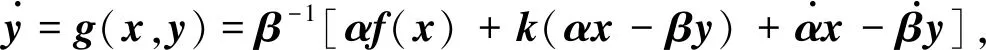
(4)

其中:β-1为矩阵β的逆矩阵;k=diag(k1,k2,…,kn)为反馈增益矩阵. 根据式(3), 驱动系统(1)和响应系统(3)的误差系统为

构造Lyapunov函数

(6)

显然,V是正定的,V的变化率为

(7)

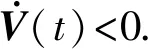
由于其他同步方式是广义修正函数投影同步的特殊情形, 因此当反馈增益矩阵正定时, 驱动系统和响应系统的其他同步方式均可实现. 上述理论适于一切连续混沌系统, 因此可选任意维数的连续混沌系统或高维超混沌系统作为驱动系统, 构造相应的响应系统, 进一步实现其广义修正函数投影同步.

3 数值仿真

本文以文献[17]研究的三维类Lorenz混沌系统作为驱动系统, 其动力学方程为

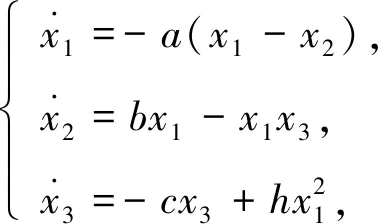
(8)

其中a,b,c,h为系统参数. 当a=10,b=40,c=2.5,h=4时, 系统(8)处于混沌运动状态. 选取反馈增益对角矩阵k=diag(a,1,c), 根据式(4)可得响应系统为

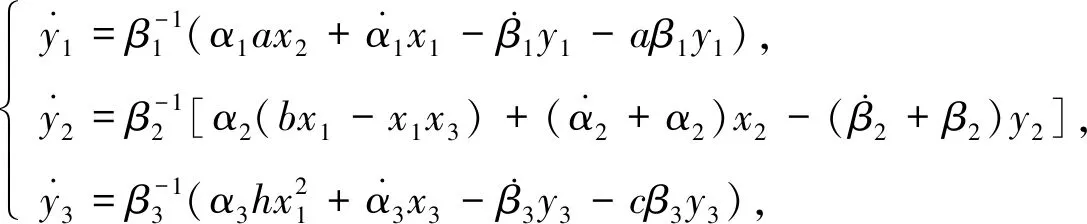
(9)

其中: 系统参数a,b,c,h与式(8)中的取值相同;y1,y2,y3为响应系统的状态变量. 显然反馈增益矩阵k=diag(a,1,c)正定, 满足实现广义修正函数投影同步的充分条件, 因此驱动系统(8)和响应系统(9)可实现广义修正函数投影同步. 任意选取比例函数矩阵α和β, 其中β的对角线元素全不为0, 不妨选α和β分别为

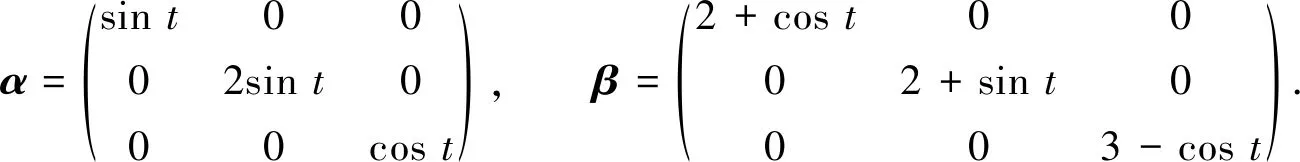
(10)

任取驱动系统(8)和响应系统(9)的初值条件分别为(x1(0),x2(0),x3(0))=(1,-1,-3)和(y1(0),y2(0),y3(0))=(2,-3,1). 利用四阶Runge-Kutta法, 可得驱动系统(8)和响应系统(9)的相图分别如图1和图2所示.

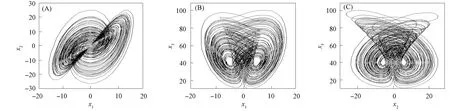
图1 驱动系统(8)的相图

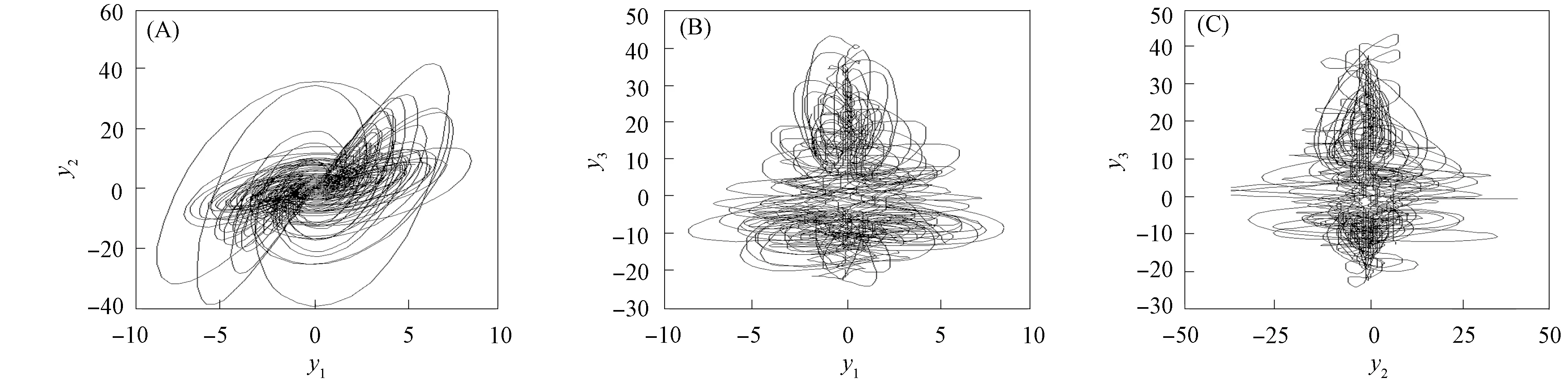
图2 响应系统(9)的相图

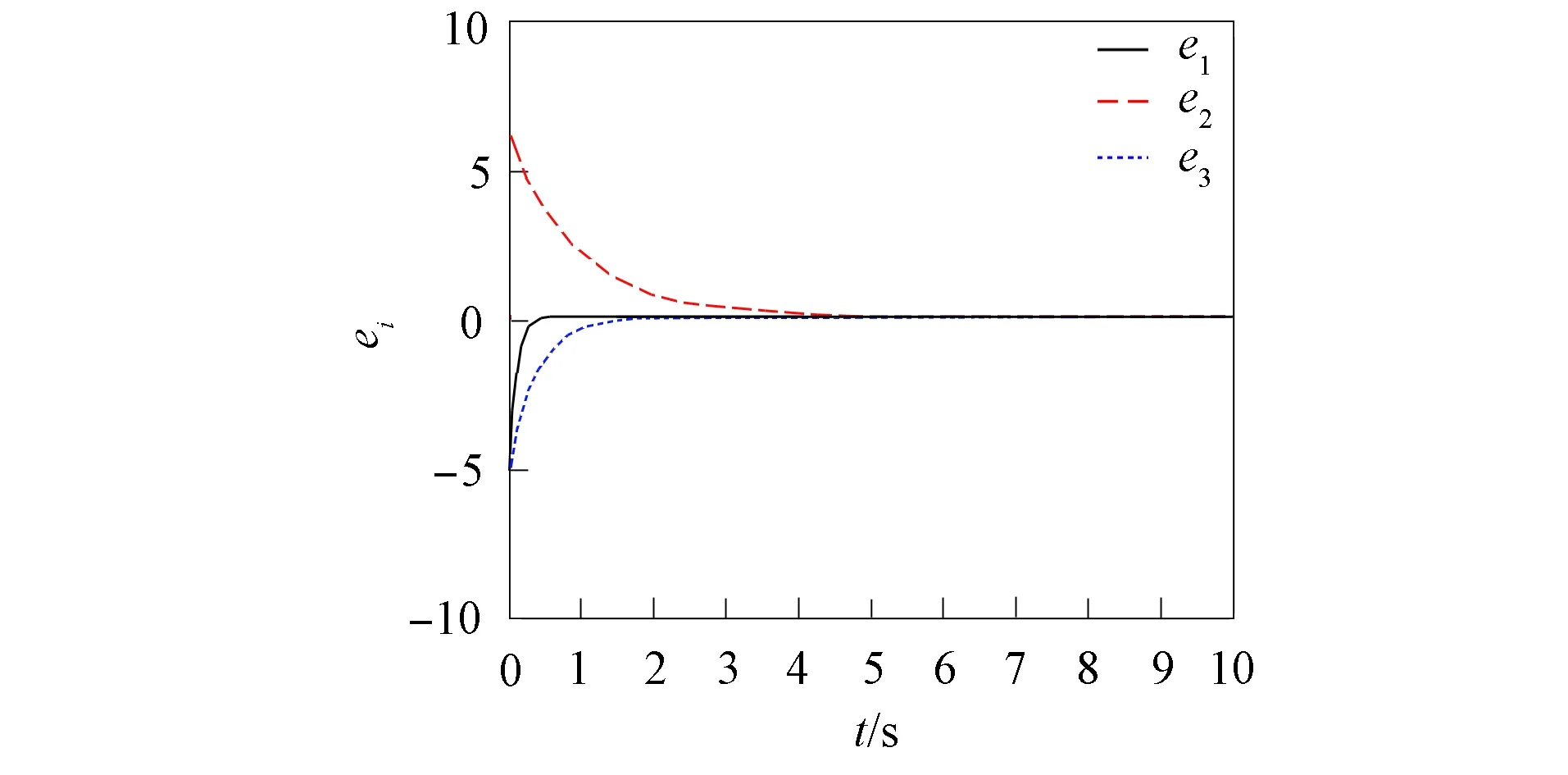
图3 驱动系统(8)和响应系统(9)的广义 修正函数投影同步误差曲线

根据式(10)可将广义修正函数投影同步误差

e=αx-βy

改写为

(11)

并仿真驱动系统(8)和响应系统(9)的误差(11), 同步误差曲线如图3所示. 由图3可见, 广义修正函数投影同步误差ei(i=1,2,3)在5 s内稳定收敛于0, 表明驱动系统(8)和响应系统(9)在5 s内实现了广义修正函数投影同步.

4 同步电路模拟

基于Multisim14电路仿真平台, 由于运算放大器TL084CN和乘法器AD633可承受的电压分别为±18,±10 V, 而系统(8)的输出电压约为±120 V, 为合理有效进行电路模拟实验, 并在电路中能观察到图像, 因此将混沌信号输出电压调小为原来的1/20, 令u1=x1/20,u2=x2/20,u3=x3/20,v1=y1/20,v2=y2/20,v3=y3/20, 变换后的驱动系统和响应系统分别为

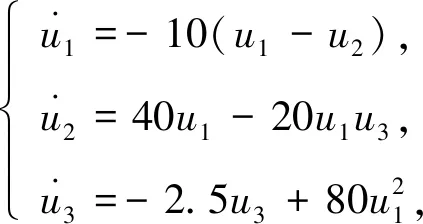
(12)

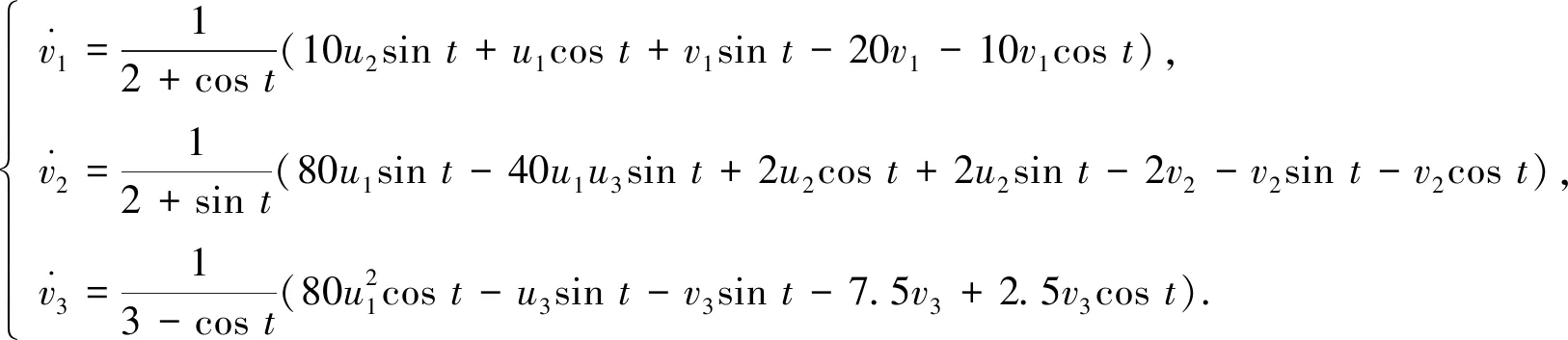
(13)

根据广义修正函数投影同步误差(11), 可得驱动系统(12)和响应系统(13)的广义修正函数投影同步误差为

(14)

为实现式(12)～(14)中的微分、 加法、 减法、 乘法、 除法和比例函数等运算, 用同相比例器、 反相比例器、 反向加法器、 积分运算器、 微分运算器、 乘法器、 除法器及函数信号发生器等构造驱动系统、 同步比例函数和响应系统的仿真电路, 仿真电路图略.

利用电路设计的模块化方法， 将驱动系统、 响应系统和比例函数的电路模块组合， 构成驱动系统与响应系统广义修正函数投影同步的仿真电路. 仿真运行驱动系统(12), 将示波器通道内的仿真数据输出到EXCEL电子表格, 并读入MATLAB软件, 绘制示波器上显示驱动系统的混沌吸引子相图, 如图4所示. 仿真响应系统(13), 将示波器通道内的仿真数据输出到EXCEL电子表格, 并读入MATLAB软件, 绘制示波器上显示响应系统的混沌吸引子相图, 如图5所示. 将图4和图5放大20倍, 结果表明, 图4和图5结果分别与数值仿真的图1和图2结果一致, 表明电路设计正确.

由于电路仿真的初值条件为原点, 示波器上显示同步误差曲线是从原点出发的一条水平直线, 因此为进一步说明驱动和响应系统的广义修正函数投影同步, 根据同步误差式(14), 电路仿真u1sint和-v1(2+cost)、 2u2sint和-v2(2+sint)及u3cost和-v3(3-cost)的时间序列波形, 如图6所示, 其中:u1sint,2u2sint,u3cost的波形用黑线表示; -v1(2+cost),-v2(2+sint),-v3(3-cost)的波形用红线表示. 由图6可见,u1sint和-v1(2+cost)、 2u2sint和-v2(2+sint)及u3cost和-v3(3-cost)的波形分别关于横轴对称, 表明驱动系统和响应系统的广义修正函数投影同步误差η1=u1sint-v1(2+cost),η2=2u2sint-v2(2+sint),η3=u3cost-v3(3-cost)均趋于0, 即电路仿真实现了驱动系统(12)和响应系统(13)的广义修正函数投影同步.

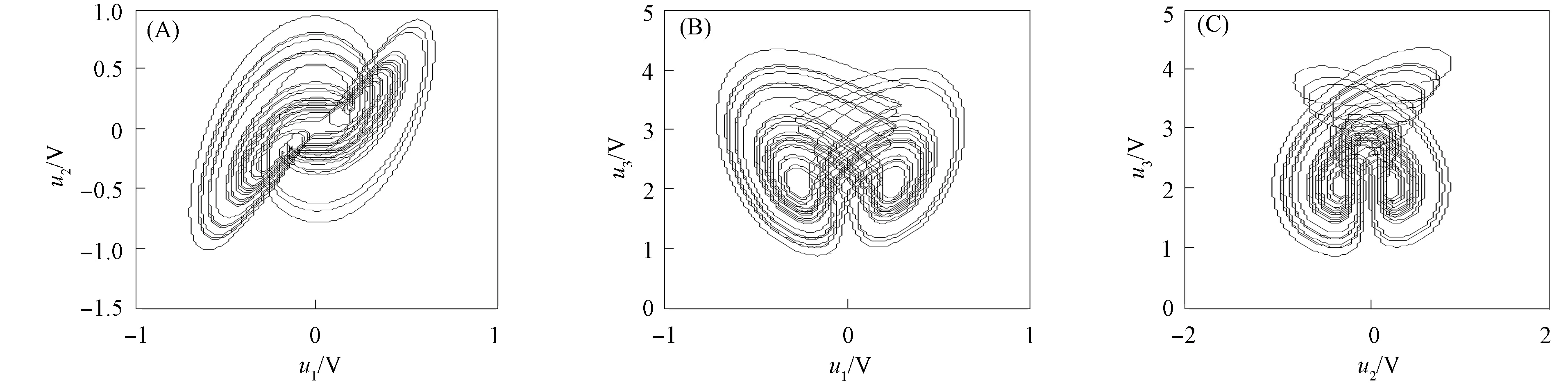
图4 驱动系统(12)在示波器上的相图

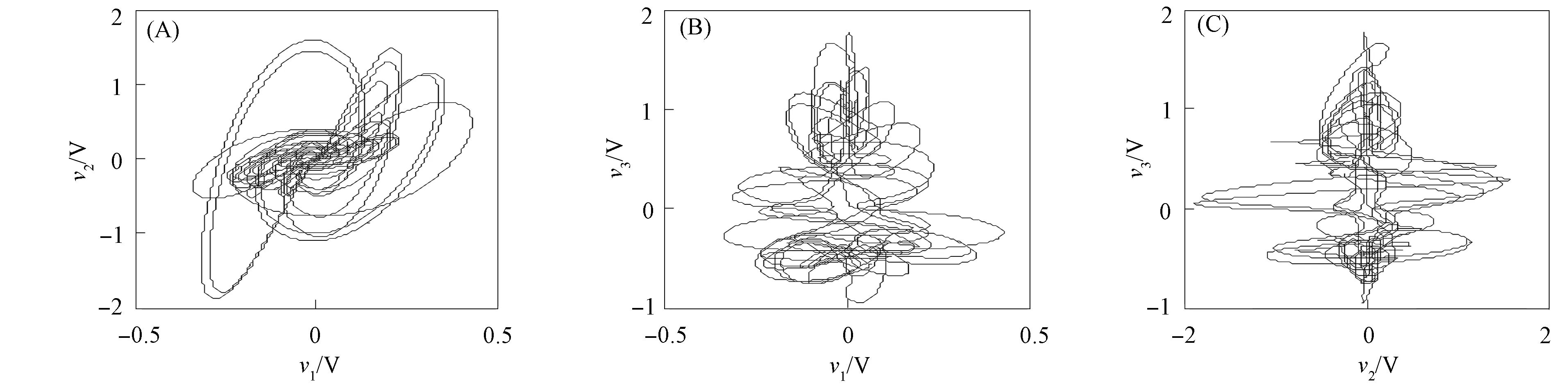
图5 响应系统(13)在示波器上的相图

图6 驱动和响应系统的广义修正函数投影同步波形

综上, 本文研究了混沌系统的广义修正函数投影同步及其电路仿真. 基于任意驱动系统的状态方程和混沌系统的单向耦合原理构造响应系统, 并通过Lyapunov函数证明得出结论, 驱动系统和响应系统可实现广义修正函数投影同步的充分条件是反馈增益矩阵正定, 实现混沌系统的广义修正函数投影同步的充分条件简单且易满足. 设计了混沌系统广义修正函数投影同步的仿真电路, 示波器输出的驱动系统相图、 响应系统相图及同步波形图与数值仿真结果相符, 表明构造的混沌系统广义修正函数投影同步电路是正确的.