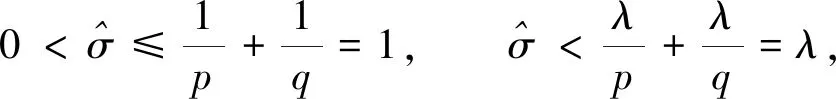一个较精确加强型的半离散Hilbert型不等式
辛冬梅, 杨必成
(广东第二师范学院 数学系, 广州 510303)
0 引 言

(1)
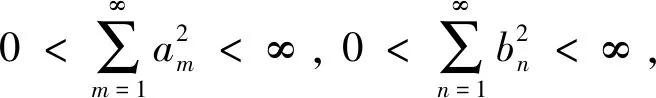

(2)
这里, 常数因子π均为最佳值. 式(1)和式(2)是分析学中的重要不等式[2-4].
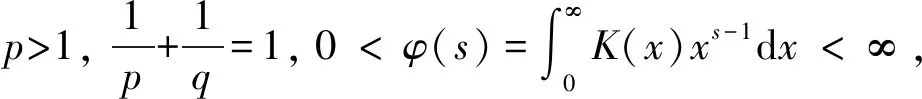

(3)
文献[5-8]给出了式(3)的若干推广和应用; 文献[9-10]讨论了式(1)和式(2)一般推广形式的常数因子取最佳值联系参数的等价性质; 文献[11]讨论了如下半离散非齐次核Hilbert不等式:
的最佳常数因子联系参数σ,σ1(∈(0,1]∩(0,λ))的等价性质, 其中
是Beta函数.
本文参考文献[9]方法, 应用权函数及Hermite-Hadamard不等式, 建立式(4)的一个较精确且加强型的不等式, 并给出该不等式常数因子取最佳值联系参数的一组等价性质及一些特殊参数不等式.
1 引 理

又设f(x)≥0(x∈+=(0,∞)),an≥0(n∈={1,2,…}), 使得
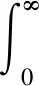
引理1若权函数
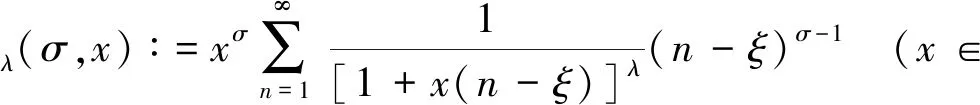
(5)
则有如下双边不等式
B(σ,λ-σ)(1-O1(xσ))<ϖλ(σ,x) (6) 其中: (7) 证明: 固定x>0, 设 这里,ρξ(x)如式(7). 事实上, 有 故式(6)成立. 证毕. 引理2下列不等式成立: 证明: 对于n∈, 做变换u=x(n-ξ), 可求得下列权函数: (9) 由Hölder不等式[12], 有 再由式(6),(9), 有式(8). 证毕. 注1因ρξ(x)≥0, 故由式(8)可导出如下非加强型不等式: 特别地, 取ξ=0, 式(10)即变为式(4). 因而式(8)是式(4)的较精确的加强型不等式. 若σ1=σ∈(0,1]∩(0,λ), 则式(8)变为如下简洁形式: 定理1式(11)的常数因子B(σ,λ-σ)是最佳值. 证明: 任给0<ε 这里, 由式(6), 因 故还可得 从而可得不等式: 令ε→0+, 由Beta函数的连续性, 有B(σ,λ-σ)≤M. 故M=B(σ,λ-σ)是式(11)的最佳值. 证毕. 且式(8)变形为 定理2若式(12)的常数因子B1/p(σ,λ-σ)B1/q(σ1,λ-σ1)是最佳值, 则σ1=σ. 由Hölder不等式[12], 有 且式(13)取等号的充分必要条件是存在不全为0的常数A,B, 使得Auσ-1=Buσ1-1a.e.于+. 不妨设A≠0, 于是有于+, 即有σ-σ1=0. 故σ1=σ. 证毕. 定理3下列陈述等价: 1) B1/p(σ,λ-σ)B1/q(σ1,λ-σ1)与p,q无关; 2) B1/p(σ,λ-σ)B1/q(σ1,λ-σ1)可表示为一个单积分; 3) B1/p(σ,λ-σ)B1/q(σ1,λ-σ1)是式(8)的最佳值; 4)σ1=σ. 证明: 1) ⟹ 2). 由于B1/p(σ,λ-σ)B1/q(σ1,λ-σ1)与p,q无关, 故 其为一个单积分. 4) ⟹ 1). 因σ1=σ, 故 B1/p(σ,λ-σ)B1/q(σ1,λ-σ1)=B(σ,λ-σ), 与p,q无关. 4) ⟹ 3). 由定理1知, B1/p(σ,λ-σ)B1/q(σ1,λ-σ1)是式(12)(即式(8))的最佳值. 3) ⟹ 4). 由定理2有σ1=σ. 故陈述1)~4)等价. 证毕. 则有不等式 (14) 则有不等式 (16) 上述不等式的常数因子都是最佳值.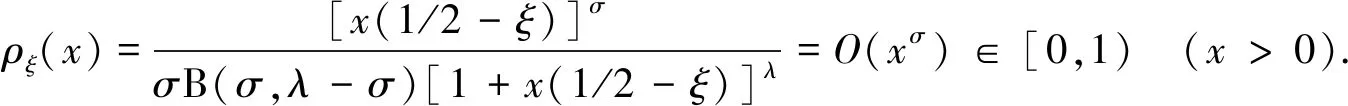
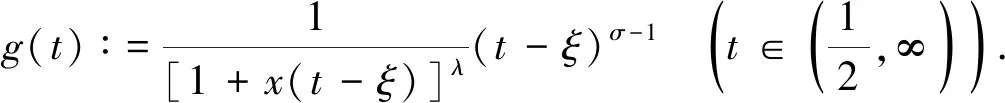
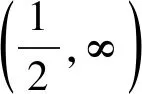

2 主要结果