常微分方程教学中逆向思维能力的培养

王艳艳

(安徽工业大学 数理科学与工程学院，安徽 马鞍山 243002)

逆向思维，也称求异思维，它是对司空见惯的似乎已成定论的事物或观点反过来思考的一种思维方式。当众人都朝着一个固定的思维方向思考问题时，朝相反的方向思索，这样的思维方式就叫逆向思维。在工科高等数学常微分方程章节的教学过程中，通常是给出一类方程后，讲解该类方程的求解方法并要求学生能熟练求解该类方程，以便在以后的解题过程中遇到该类方程就可以得心应手地解决，从而节省时间和精力，这就是应用了思维定势的正效应。但是，思维定势的存在也会束缚我们的思维，使人们只用常规方法去解决问题，因而会给解决问题带来一些消极影响，对创新会起到阻碍作用，容易使人养成机械地、呆板地解决问题的习惯，从而妨碍人们充分发挥自己的主观能动性去灵活思考和解决问题，这也正是过去存在所谓“高分低能”现象的根源所在[1]。在讲授常微分方程章节时利用逆向思维去思考和处理一些特定的数学情景、数学题型，可以帮助学生开拓视野，打破思维定势，以“出奇”达到“制胜”，从而拓宽学生的思维，训练其思维能力。

一、整体章节对逆向思维的培养

在研究客观事物的规律时，常常需要研究反映客观事物规律的那些量之间的函数关系。但在很多情况下，很难直接找出这些函数关系，而是建立函数及其导数或微分之间的关系式，这就是微分方程。其理论及方法是解决几何学问题、物理学问题和其他各类实际问题的重要数学工具。目前，微分方程在自动控制、弹道设计、飞机和导弹飞行的稳定性等许多领域都有极其广泛的应用。在高等数学常微分方程章节的教学过程中，常微分方程求解的最根本的思想就是求导或微分的逆运算，即逆向思维的使用。在学习常微分方程之前，学生已经掌握了给定函数如何求出其导数或微分。而在常微分方程中，问题变成借助函数的导数或微分，反其道而行之来确定函数或函数族。在本章节的教学之初，给学生提出这样一个问题：已知函数是y=x2,其导数或微分是多少？

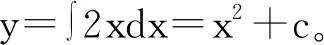
二、例题教学对逆向思维的培养

在常微分方程章节的教学过程中，我们的教学模式通常是介绍一类方程，然后讲解该类方程的求解方法，比如，在介绍二阶线性常系数方程的通解时，我们都是按照先介绍如何求二阶常系数齐次线性方程的通解，再讲授如何求二阶常系数非齐次方程的特解，从而二者相加得到所求非齐次通解，这是正向的思维。然而该章节的很多题型却并不是直接的正向思维的题型，必须借助逆向思维才能解决。

1.借助通解给出微分方程

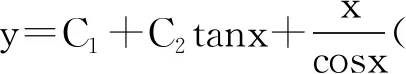
(A)sinx·y″-2cosx·y′=x

(B)cosx·y″-2sinx·y′=x

(C)sinx·y″-2cosx·y′=0

(D)cosx·y″-2sinx·y′=0

在常微分方程章节的学习中，学生比较习惯的思维是给出方程，求其通解或特解，而这样一个选择题却反其道而行之，把通解作为已知条件来找合适的方程，这就打破了学生的正向思维。在该题中，所给的方程学生是无法求解的，只能通过逆向思维，根据通解判断出选项(B)正确，从而强化了逆向思维。

2.已知特解求方程

例2 某四阶常系数齐次线性微分方程的两个特解y1=xex和y2=sinx，求此微分方程[2]。

解：由解的结构以及y1=xex为方程的解可知r1=1至少为特征方程的二重根。

由y2=sinx是方程的一个特解可得r3=i,r4=-i至少为特征方程的一对共轭复根。而四阶常系数齐次线性微分方程的特征方程在复数范围内只能有4个根，故所求方程的特征方程为

(r-1)2(r-i)(r+i)=0,

展开后借助特征方程和微分方程的一一对应，得到所求方程为

y(4)-2y″′+2y″-2y′+y=0

在该例题中，将求高阶常系数齐次方程通解的通用方法反过来使用，充分使用了逆向思维，使问题得到快速解决。该题求解过程中的每一步思路都用到了逆向思维。求解过程的第一步是通过特解得到特征根，这正是高阶常系数线性微分方程求解方法中通过特征根给出相应特解的逆运算。在高阶常系数线性微分方程求解方法中首先就要根据微分方程写出其对应的特征方程，而解题过程中的第二步通过特征方程从而得到常微分方程恰恰就是该过程的逆运算。逆向思维的使用在该题型中得到了充分的训练。

3.逆向思维求特殊方程的解

例3 解微分方程[3]

y″+2y=sinx,y(0)=0,y′(0)=1

对该题常规的解法是根据其对应的齐次方程，给出特征方程，求出特征根，给出两个线性无关的齐次特解，从而得到齐次通解；再根据方程右端和特征根，形式地给出该方程的一个特解，利用待定系数法确定该特解，从而得到所给方程的通解；最后根据定解条件确定所求通解中的两个任意常数，从而解决该问题。这种解法计算量相对比较大，计算步骤较多。而利用逆向思维，借助方程特点及方程与特解间的常见联系，可以预估出该问题的特解具有y=csinx的形式，再回归方程确定c=1，从而使问题得到轻松解决。通过这样的题型设置会让学生对逆向思维的出其不意有深刻的印象，从而在强化逆向思维的同时也引导了学生主动使用逆向思维的兴趣。

4.提高方程的阶数来求解方程

对于高阶方程，除了线性方程，都会考虑能否将其阶数减低，甚至降到一阶方程，通过低阶的解从而得到高阶方程的解。而对于一阶微分方程，直接的反应就是根据方程特点直接求解，几乎不会考虑将其从一阶方程变成高阶方程来求解。然而，对于一些特殊的一阶线性微分方程，升阶法也是行之有效的方法。

例4 解一阶线性微分方程[4]

y′+y=e-x

对于该方程，学生脑海中的第一反应就是通过公式或常数变易法给出其通解，但是在这两种方法之外，升阶法同样可以解决该问题。其思路是将所给的一阶线性微分方程转化为二阶常系数齐次线性微分方程，再借助特征方程和特征根给出该二阶方程的通解；将该通解带入原始方程从而确定原始方程的通解。这种方法虽然适用的范围有局限性，但是它打破了一成不变的降阶法，引导学生从多角度、多方位考虑问题，训练了其逆向思维。

三、结语

在高等数学的学习中，学生优先接触的都是正向的运算，在大量正向思维的训练下，在解决问题时逆向思维难以发生。而常微分方程章节的教学可以弥补这样的不足，该章节本身就是微分运算的逆运算，整个章节都需要用到微分的逆运算，从而自始至终地引导学生建立逆向思维，而在上述具体问题中，更加强化了逆向思维的训练，培养了学生逆向思维的能力，加深对问题的认识，使其能够在解决问题时获得最佳的途径和方法，能够摆脱思维的僵化和刻板，新颖地处理问题，把学生的思维带入更广阔的佳境，使思维更加开放、扩散。