SIFT算子与改进算法检测木板条纹的对比研究

张发军 宋钰青 邓安禄 虞成俊 彭文刚

(1.三峡大学 机械与动力学院， 湖北 宜昌 443002；2.水电机械设备设计与维护湖北省重点实验室， 湖北 宜昌 443002)

木板是木材加工后形成的，其纹理年轮会形成条纹，使得木板的表面呈现线状分布.木板条纹的粗细会影响材料的美观，即使是同一种木板，条纹的粗细也会影响其商用价值.如今工厂大多数都是靠人工分拣，效率低下，准确率不高，故实现木板条纹检测的自动化对工厂加工具有重大的实用价值和意义.目前的研究主要集中在木材的缺陷和纹理的分类检测[1-2].文献[3]提出基于深度学习的木材缺陷图像检测方法，该方法通过训练卷积神经网络与CV分割算法组合，能较强地定位缺陷位置，但此方法需要大量的训练样本，算法效率不高.文献[4]提出应用灰度直方图的平滑度特征来识别木材表面缺陷，识别率高于99%且效率高.文献[5]提出基于灰度共生矩阵和模糊BP神经网络的识别算法，该算法需要训练，算法复杂，识别缺陷的成功率不如上述文献.

对于上述木材缺陷算法的研究，深度学习和神经网络算法因其算法复杂，需要提取多种特征值，有的甚至可达几十个，训练费时，且效率不高，不适合运用在条纹检测的自动化中，因此需要用少量的特征来高效地表达木板条纹.而灰度直方图算法简单，基于这一想法，本文提出一种灰度直方图改进算法来检测木板条纹.而目前最常见的纹理检测为图像增强、边缘检测、图像分割算法、直线检测算法.文献[6]采用灰度TV滤波，模糊区域竞争模型进行图像分割.这种算法的边缘定位能力不高，且适用性不确定.直线检测算法为霍夫变换和霍夫概率变换.这两种算法首先需进行高斯平滑将原图像降噪，再进行Canny边缘检测，最后进行霍夫直线检测或霍夫概率直线检测[7].这种算法对轮廓清晰，条纹深浅差距较大的木板效果是特别好的，设置能将条纹的上下轮廓提取出来.但是，对条纹深浅差距特别小的木板，效果则特别差.因为在Canny边缘检测这一步，原图像的灰度图像各个像素点之间的值差距是比较小的，且条纹之间有与条纹相近的噪点，所以无法通过Canny边缘检测的阈值调节来分离各个条纹，出现的是无序的边界点.而霍夫概率是在霍夫变换的基础上，对边界点进行随机采样，在直线到原点距离和直线角度形成的累加器空间进行投票，达到阈值则认为有直线.但无序的边界点会极大影响其结果，无法通过阈值来判断直线的真假.而对图像进行形态学分割也只适用于条纹清晰的木板，适用范围窄，不能用于工厂的自动化.

为了检测木板的条纹，将条纹定为特征，为准确寻找图像中的特征点，本文提出一种改进直方图算法，利用python编程，与David Lowe提出的SIFT算法和直方图算法对比来分析其效果[8].

1 SIFT算法检测条纹

SIFT算法即尺度不变特征转换，是通过在尺度空间内找寻不会对旋转、尺度缩放、亮度变化而产生变化的特征点[9-10].SIFT算法是通过高斯卷积核来对图像进行高斯平滑，然后在此基础上进行尺度的变换，高斯卷积核公式为

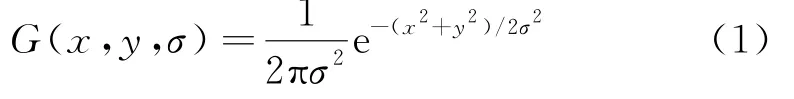
1.1 构造尺度空间

1)利用双线性插值将源图像放大一倍，再进行σ=1.62-(0.5×2)2的高斯模糊，生成基础图像.其中初始σ=1.6.

2)计算高斯金字塔组数n，每组图像的长度和宽度为下一组的两倍，并使得顶组的图像长宽在8像素左右.

3)构造高斯金字塔.每组有(s+3)层，第(s+1)层图像为下一组的第一层图像.每一层高斯模糊参数

4)构造差分高斯金字塔.将每组的高斯金字塔图像相减，得到n组(s+2)层差分高斯金字塔.高斯差分算子为：

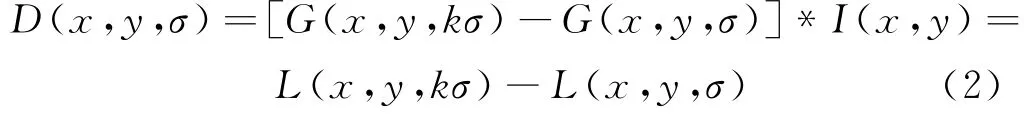
其中I为原图像.

1.2 找寻尺度空间特征点

1)找寻极值点.将图像的像素点与前后两幅图像与自身周围共26个邻域像素点比较，记录极值点.

2)对极值点精确.离散空间的极值点并不是真正的极值点.利用子像素插值得到真正的极值点.

对尺度空间DoG函数进行曲线拟合，其Taylor展开式为：

其 中X=(x，y，σ)T.

对其求导，令方程等于零可得到

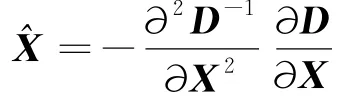
其对应的方程值为：

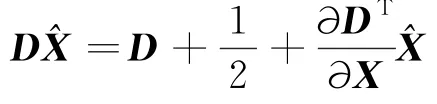
3)过滤掉边缘点.利用Hessian矩阵H的轨迹和行列式，去除不稳定的边缘响应点.

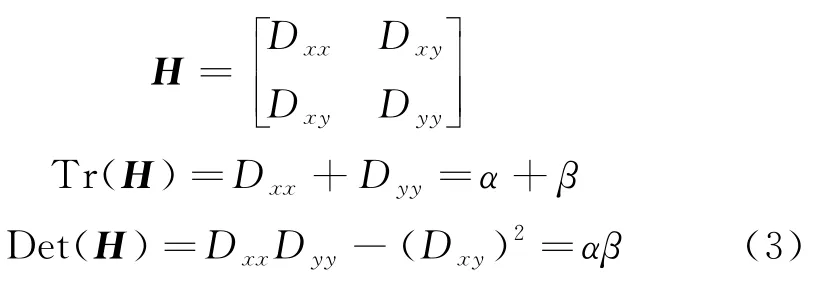
其中α为H的最大特征值，β为H的最小特征值，令α=rβ，则

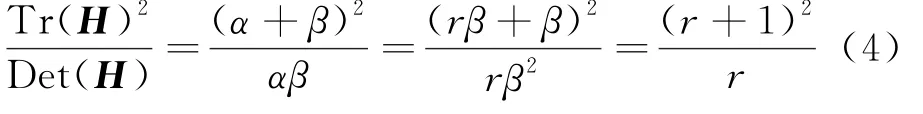
D的主曲率和H的特征值成正比，则公式(r+1)2/r的值在两个特征值相等时最小，随着r的增大而增大.(r+1)2/r值越大，说明两个特征值的比值越大，即在某一个方向的梯度值越大，而在另一个方向的梯度值越小，而边缘恰恰就是这种情况.所以为了剔除边缘响应点，需要让该比值小于一定的阈值，因此，为了检测主曲率是否在某阈值r下，取r=10，若

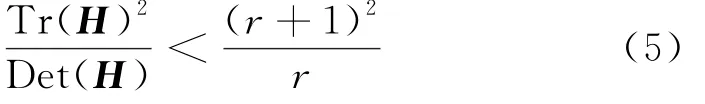
则特征点保留.

该算法所得特征点如图1～2所示.从图1可看出，SIFT算法对条纹较清晰的木材特征点找寻是很精确的，但在图1所示的最左侧，可以发现特征点的找取是不准确的，反光还是会对其产生影响.如图2所示，SIFT算法对条纹不清晰的木材的特征点找寻则十分不理想，准确率达不到50%，且对于样板3、4完全找不到特征点.故此方法不适用.

图1 SIFT算法特征点

图2 SIFT算法特征点效果图

2 灰度直方图检测条纹

灰度直方图则是通过叠加每行像素的灰度值，通过每行灰度总值的变化来找寻特征点.对于条纹较浅的木板，这样可以加深特征.

而对灰度直方图算法来说，如何消除干扰点是一个难题.如果只是找寻极小值，一张图片就存在上百个极小值点，如图3所示.本研究需要的是在某一局部的最小，而每一个木材的条纹数是不确定的，故局部范围不能确定.

图3 灰度直方图极小值点

从图3可看出，所需要的特征点在这些极小值点中，但这些极小值点分布特别密集，可以通过设定阈值，使得下一个极小值点的像素位置减去该极小值点像素位置大于某一阈值的极小值点，则判断该极小值点为所需特征点.具体步骤如下：

1)对灰度图像进行分段，每100列像素点为一段，计算每行像素点的灰度值之和，如图4所示.

2)记录极小值所在的点及其值.

3)寻找特征点.如果极小值点减下一个极小值点的值大于某个阈值，则判断该极小值为所需的特征点.

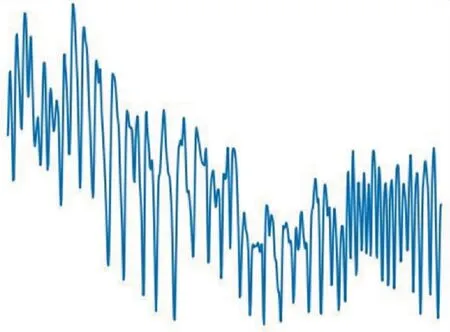
图4 灰度直方图

从图5与图6可以看出，该方法很不稳定，并没有很好地把特征点提取出来，还是存在很多干扰点，且阈值要手动设置，不同的阈值对结果影响很大.过小无法消除干扰点，过大则错过了特征点.

图5 浅条纹样本灰度直方图算法特征点

图6 深条纹样本灰度直方图算法特征点

3 改进灰度直方图检测条纹

3.1 改进灰度直方图法

灰度直方图的所有极小值之中一定包含所需要的特征点.由于木材的纹理不平滑会产生干扰点，可从图4看出这些干扰点会在真正的极小值点附近波动.这些干扰点与下一个极大值的距离是远小于真正极小值点与下一个极大值点的距离的.因此通过设定阈值可以较好地消除干扰点.具体步骤如下：

1)对灰度图像进行分段，每100列像素点为一段，计算每行像素点的灰度值之和，如图4所示.对图像分段进行灰度值累加是为了确保能够准确将条纹分离出来，拉大灰度直方图的相邻极大极小值的差.灰度值越小则图像越黑，累加之后有条纹的区域的值会处于极小.

2)分别记录极大值和极小值所在的点及其值.

3)设定阈值.记录极大值点的值减下一个极小值点值的绝对值.如果大于阈值，则判断该极小值为所需的特征点，如图7与图8所示.其中，阈值为所有极大值减相邻极小值的差值由小到大排序后位于80%位置的差值的1/3.

图7 浅条纹样本改进灰度直方图算法特征点

图8 深条纹样本改进灰度直方图算法特征点

图1与图2所示为SIFT算法找寻的特征点，图7与图8所示为改进灰度直方图找寻的每段的特征点.通过对比可以看出，对于条纹清晰的木板SIFT算法和改进直方图算法的效果类似，都对左侧存在反光的区域无法准确找寻，在光线稳定的区域特征点找寻准确率可达90%以上；对于条纹不清晰的木板SIFT算法则比改进直方图方法差得多，大部分条纹的特征点如图2无法标记，而改进直方图方法能很好地标记出特征点.通过改进的直方图方法对样板进行处理得到其准确率及偏差率，见表1.条纹检测的准确率=特征点在条纹上的个数/条纹个数.偏差率=特征点不在条纹的个数/条纹个数.

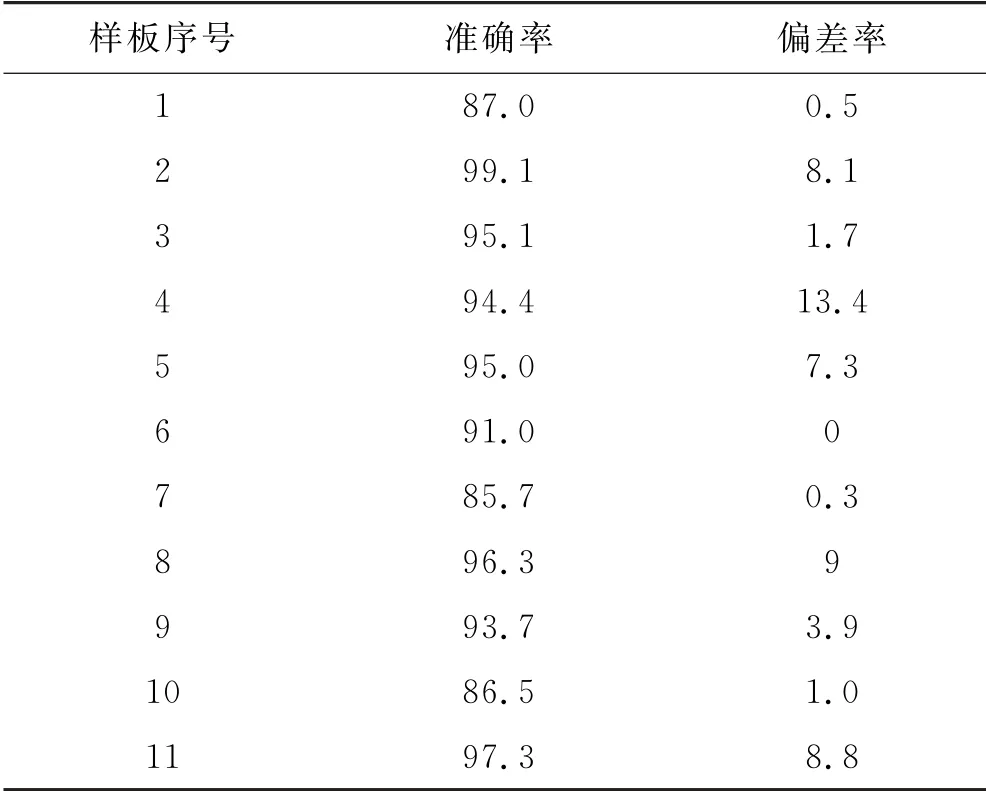
表1 样板的准确率及偏差率 (单位：%)

随机选取11张样板进行测试，样板原图如图9所示，改进的直方图效果如图10所示.对于条纹特征明显的木板如样板2、3、4、5、8、11，检测的准确率可达94%以上.但是样板的色度不均性会模糊条纹边界，对偏差率影响较大，如样板4和8.对于条纹极细的样板如1、6、7、10，有的条纹边界模糊，几近没有条纹，但是改进直方图算法还是可以较好地检测出来，准确率可达85%且偏差率在1%以内.对于条纹特征不太清晰，但条纹间距较大的木板如样板9，其准确率有93.7%，偏差率3.9%.

图9 样板原图

图10 改进直方图效果图

3.2 改进灰度直方图法的方向性

上述灰度直方图法只能对斜率在±10°范围内的木板进行条纹检测，故需要对木材的图片预先进行旋转，才能较好地进行检测.

木板的纹理是由均匀的直线分布而成，为了能将这些直线旋转成斜率在所需范围内，首先需要检测这些条纹斜率的大概范围.

GLCM(灰度共生矩阵)可以描述具有某种空间位置关系两个像素灰度的联合分布.根据这一概念，先把图像的像素分为两级.木板有条纹的部分灰度值较深且出现的概率比其他的灰度低，因此将灰度值按从小到大的顺序寻找到其概率刚好大于等于0.005的灰度x，这个灰度x就是所需的分割点.再将小于该分割点的灰度值改为0，其他的改为255，得到二值图像，灰度级为2，如图11所示.最后将通过循环法寻找相同元素出现的次数，该次数与循环次数的比值为所需的值.如斜率为零，则通过对比该像素点和往右的第10个像素点的值是否一样；斜率为无穷，则通过对比该像素点和往下的第10个像素点的值是否一样；斜率为45°，则通过对比该像素点和往左10个像素点再往下10个像素点的值是否一样.

图11 灰度级为2的二值图像

从样板中随机选取10张图片，如图12所示.对其旋转一定角度进行方向性测试，结果见表2.其中概率数值最大的角度为该木板的斜率，可以发现所测试的10张图片中的方向性准确率可达91%.通过同一块木板不同斜率的概率值可以发现最大与最小的概率值相差不是特别大，特别是条纹细密的木板，如样板4.

图12 测试图片

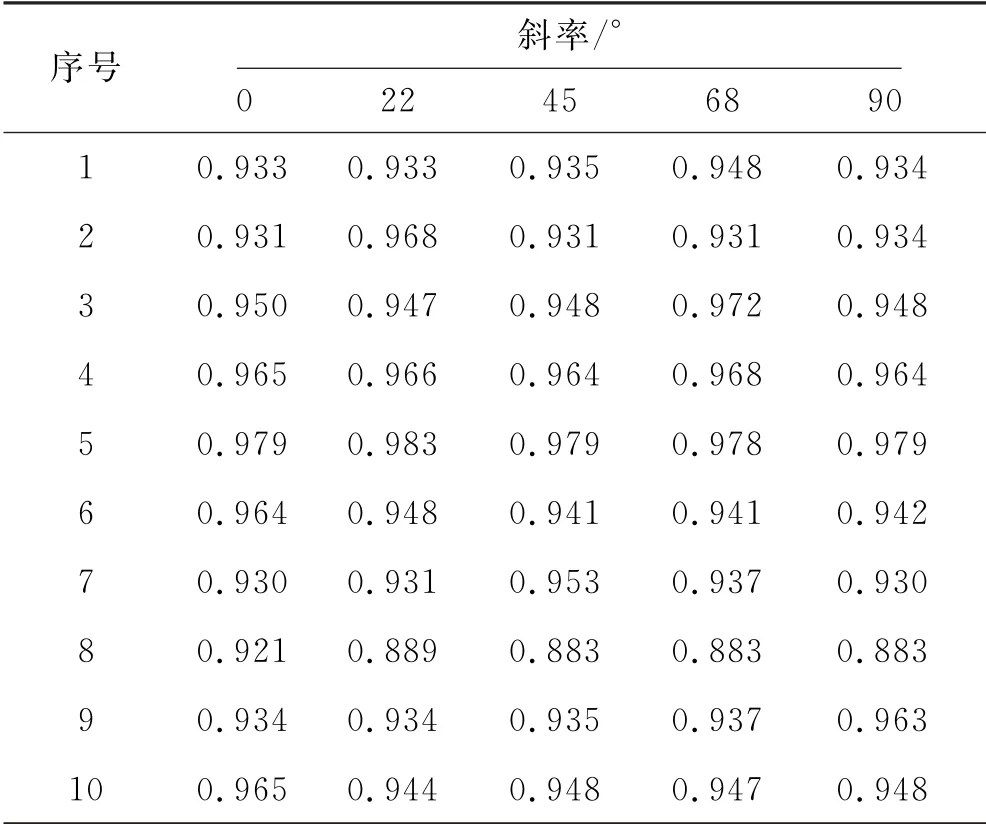
表2 测试图片方向分布特征值

木板方向性准确率高的前提是光照均匀，否则会极大影响二值化的图像，使得二值化后的图像条纹没有规律性、方向性.

4 结 论

通过对木材图像进行SIFT算法和改进直方图算法得到的特征点，可以看出：

1)改进直方图算法相比SIFT算法在木材条纹检测上更有效，算法更加简单，故具有可行性，对木材条纹的检测有较好的指引作用.

2)改进直方图算法是对某一段灰度值的横向相加，其分析的是横向条纹的检测，对斜率在±10°范围内的条纹还是可以检测的，但通过方向性可以确定其大概的斜率范围，将其旋转之后再进行检测，可大大提高准确率；光照不均，反光大则会影响其结果，因此，在今后的实验中可对其方向性做进一步的改进.