流场可压缩性对涡相互作用影响的数值研究

郑忠华，范周琴，王子昂，余彬，张斌,*

1. 中国空气动力研究与发展中心 超高速空气动力研究所 高超声速冲压发动机技术重点实验室，绵阳 621000 2. 上海交通大学 航空航天学院，上海 200240

作为一类基础流动模型，两个同向旋转涡旋之间的相互作用首先由飞机尾迹涡系抽象提出[1]。研究表明，合理控制外部自由来流经过机翼产生的尾迹相互作用不仅有助于减小诱导阻力，更能从涡系不稳定性的角度将尾迹对周围气流扰动的影响降至最低，提高飞行安全性[2]。除广泛实际工程应用外，深入认识涡相互作用流动机理对理解剪切层、湍流等流体前沿难题同样具有重要科学意义，至今已吸引众多顶尖学者通过实验[3]及数值手段[4]进行研究。

首先，针对涡旋发生相互作用的条件，Saffman和Szeto[5]提出两个涡旋距离与涡旋半径之比(定义为涡对展弦比)是决定涡对内部应变强弱的重要参数。Melander等[6]对两个涡量均匀分布的涡旋进行数值模拟，发现涡相互作用发生的临界条件为涡对展弦比在0.3左右。Meunier等[7]通过涡旋旋转角动量构建涡旋有效半径的概念，理论推导指出涡对临界展弦比范围为0.22～0.26且与涡旋雷诺数以及具体涡旋类型无关。关于涡相互作用的物理机制，Melander和Mcwilliams[8]在与涡对同速旋转的参考坐标系中通过流线观察涡相互作用过程指出虚拟涡旋(Ghost Vortex)与悬臂(Filament)形成是推动涡心相互靠近的无黏机制，并将涡对融合归纳为对称-反对称-再对称的过程。在此基础上为定量描述涡对靠近的快慢程度，Williamson[3]将涡量场分解为对称分量与反对称分量并证明涡对靠近的速度仅由反对称分量诱导决定。涡量分解理论描述的涡对间距演化规律与模拟结果吻合良好。关于涡相互作用流动特征的详细研究进展可参考Leweke等[9]的综述文献。

区别于外部尾迹流动速度远低于声速的不可压缩流场特征，以冲压发动机为代表的内部流动轴向速度接近甚至远远超过当地声速[10]，随之而来的强可压缩性对流场演化过程的影响不可忽略。针对如何将燃料与氧化物有效混合燃烧这一长期制约冲压发动机性能的核心问题[11]，近几年，利用涡相互作用过程中引入的应变作用提出了一种新型塔式燃料喷射可以有效将燃料通过涡流发生器卷入涡中，从而达到与周围空气混合增强的效果[12-13]。在此工程背景与实际需求下，研究流场可压缩性对涡相互作用过程的影响这一基础理论问题对优化设计塔式燃料喷射装置具有一定借鉴意义。本文基于可压缩Navier-Stokes方程求解算法，结合可压缩压力泊松方程设置初始条件模拟不同马赫数涡对的相互作用过程，通过比较流动结构及动力学特征的异同，重点探索可压缩性对涡相互作用流场演化过程的影响，并在此基础上初步提出服务于工程设计的可压缩时间尺度修正关系。

1 数值模拟方法

1.1 流动控制方程与数值方法

涡相互作用问题流场演化的控制方程是可压缩黏性Navier-Stokes方程，其在二维流动中表达形式为

(1)

式中：U代表由守恒参数组成的向量；向量场F、G和Fv、Gv分别代表对流通量和耗散通量，且

U=[ρ,ρu,ρv,ρE,ρY1,…，ρYNS-1]T

F=[ρ,ρu2+p,ρuv,(ρE+p)u,ρ1u,…,

ρNS-1u]T

G=[ρ,ρv2+p,ρuv,(ρE+p)v,ρ1v,…,

ρNS-1v]T

(2)

式中：ρ、p、E分别代表混合物密度、压力、单位质量总能量；u和v为混合物速度矢量的两个分量；ρi和Yi为组分i的密度和质量分数；NS为总组分数。黏性力τ和热流量q为

(3)

其中：T代表温度；H代表比焓；μ和λ分别代表气动黏性和混合物热传导率，由Wilke 半经验公式计算得到；对于高速流动问题，质量扩散系数Di为

(4)

二元扩散系数Dij为

(5)

其中：Xj为组分j的摩尔分数；文中假设施密特数Sc取0.5[14]。引入理想气体状态方程封闭方程组：

(6)

式中：Ru为普适气体常量；Mi为组分i对应的分子量。总能量E包含气体动能及气体内能，即

(7)

cpi=Ru(a1i+a2iT+a3iT2+a4iT3+a5iT4)

(8)

其中：系数a1i,a2i,…,a5i可以由权威的NASA 热力学参数数据库查得。上述数学模型在无量纲后通过有限体积法进行离散。时间推进采用三阶精度的TVD Runge-Kutta方法，对流项采用五阶WENO格式离散[15]，黏性项采用中心差分法离散。

1.2 基于可压缩压力泊松方程设置的初始条件

在基于Navier-Stokes方程的非定常计算中，初始压力场设置对模拟结果至关重要。不合理的初始条件设置会在流场演化初期额外引入非物理的噪声转捩，由此可能导致完全错误的后续流场发展过程[16]。本文考虑两个完全相同(强度、有效半径均相等且旋转方向相同)Lamb-Oseen涡之间的相互作用过程。初始速度场由每个涡旋各自依据Biot-Savart定律的诱导速度场叠加而成：

(9)

式中：r1与r2为流场中某一点到两个涡心的距离；(x1,y1) 与(x2,y2)为两个涡心的空间位置；Γ为单个涡旋强度；涡旋有效半径[7]a为

(10)

其中:ω为涡量；r为到涡心的空间距离；A为积分区域。在给定初始速度场基础上，初始热力学参数分布基于压力泊松方程结合等熵流动假设构建。该方法首先由Harlow和Welch基于不可压缩Navier-Stokes方程组推导提出并应用于不可压缩流动模拟中[17]，具有不可压缩条件内在相容、数值计算稳定、方程形式简洁易于构造高精度格式等优点。在忽略黏性项与非定常项后压力泊松方程可直接应用于初始条件设置中，具体形式为

P,ii=-ρ0ui,juj,i

(11)

式中：求和记号为爱因斯坦标记法。在不可压缩流场中，密度变化不大，近似为一常数ρ0。

在可压缩流动中，为尽可能消除流场演化初始阶段由于压力场与速度场不相容导致的噪声转捩现象，通常假设初始流场满足等熵假设[18]。另外联立可压缩压力泊松方程求解获得所有初始热力学参数分布：

(12)

根据等熵条件，压力与密度之间存在如下联系：

(13)

关于泊松方程数值算法，采用文献[19]中的紧致差分格式进行离散求解。在二维矩形网格(x及y方向上的网格精度分别为h和k)上考虑含源项f的泊松方程，形如：

φxx+φyy=f(x,y)

(14)

基于Keriss紧致差分公式[20]，可以得到九结点矩形网络下的高精度优化差分格式为

(15)

式中：r=h/k依赖于x与y方向上网格精度；上标n代表第n次迭代的值。泊松方程求解离散网格编号示意图如图1所示，算法的具体构造细节详见文献[19]。在每次迭代中均需调用一次压力边界条件完成全场计算，最后以相邻两次迭代中全场最大压力变化Δpmax<10-6为判据认为迭代收敛，终止计算。

图1 泊松方程求解离散网格编号示意图

1.3 数值验证

为验证上述Navier-Stokes非定常模拟算法与初始条件设置对模拟涡相互作用问题的有效性，采用文献[21]中的算例进行数值验证。初始涡对几何参数、涡量分布形式、计算域大小及网格精度均与文献[21]相同。初始热力学参数分布通过求解压力泊松方程设置。本文模拟流场演化过程与文献中大涡模拟结果对比如图2所示。在两个涡旋相互连接靠近的过程中涡对发生扭曲变形并向外传输涡量形成悬臂结构。在黏性扩散作用的推动下两个涡旋中心逐渐合并最终融合为单个涡旋。

另外，本文根据涡对间距与涡旋有效半径(根据式(10)计算)随时间的演化规律定量反映计算结果与文献之间的差异，如图3所示。可以发现在演化前中期本文涡对间距与涡旋有效半径计算结果均与文献吻合良好(最大误差不超过5%)，在演化后期(无量纲涡对间距b/b0<0.3)由于涡对充分靠近难以准确识别涡心位置。此时根据式(10)计算的数据无法真实反映涡旋有效半径，不再具有参考比较意义。总体而言无论是定性的涡量场发展过程还是定量的涡对几何参数演化规律都基本证明本文采用的数值方法可用于研究涡相互作用物理问题。

图2 本文数值模拟涡量云图与文献结果对比

图3 无量纲涡对间距、涡旋有效半径数值验证与文献结果对比

2 算例设置条件

控制涡相互作用进程的3个重要无量纲参数分别为：涡对展弦比、涡旋雷诺数与涡旋马赫数[4]。其中，展弦比决定涡对的几何构型，而雷诺数与马赫数反映流场演化的动力学机制。本文重点聚焦的问题是可压缩效应对相同强度涡相互作用过程的影响，因而在保证涡对展弦比与雷诺数不变的情况下，通过改变涡旋马赫数以调整流场可压缩性。为在清晰呈现结果的前提下节省计算资源，所有算例选取初始涡对展弦比为0.177，涡旋雷诺数为5 000，以避免相互作用进程过于冗长。另一方面在该雷诺数下椭圆不稳定性主导的湍流三维效应尚不显著[22]，只适用于二维数值计算方法。本文模拟算例的计算域及计算条件如图4所示，其中涡旋模型为Lamb-Oseen涡，涡量分布为

(16)

式中：U0为涡内最大速度，在涡核半径r0处取得。涡旋强度以环量Γ描述；涡旋马赫数及雷诺数可分别定义为

图4 计算域及模拟条件设置

Ma=U0/c∞

(17)

式中：c∞为无穷远处声速。

ReΓ=Γ/υ

(18)

式中：υ为流体动力黏度。

计算域大小及网格解析度对于模拟涡相互作用同样具有显著影响。采用均匀网格进行数值计算(网格精度Δx/b0=Δy/b0=0.01)，计算域大小为20b0×20b0且计算域边界均设置为外推条件以消除壁面效应对结果的潜在作用[17]。时间步长为Δt=10-9s。经过验证，该网格精度与时间步长能够保证充分的空间与时间离散，基本能够消除数值黏性对结果的影响。

3 结果与讨论

3.1 不同马赫数涡对融合演化过程

不同马赫数涡对的涡量场形态演化过程如图5所示。为保证算例结果之间的对比性与普适性，物理时间采用无量纲化处理:

(19)

式中：特征时间t*的物理意义是两个具有相同强度Γ、相距b0的点涡在无黏环境中相互旋转运动的周期；T*为无量纲演化时间。可以发现，不同马赫数涡对相互作用进程总体相似：首先在黏性扩散的作用下涡旋半径逐渐增加，此时涡对仅呈现细微的变形且两个涡旋在空间中没有直接接触(T*=0.41)；当涡旋半径不断变大与涡对间距之比达到临界阈值后，涡对系统开始融合。此时两个涡旋已相互连接并受相互诱导的应变作用发生扭曲变形，部分涡量在旋转速度场下向外输运形成典型的悬臂结构。在整个发展过程中流场均保持中心对称特征。另一方面，在相同无量纲时间下不同马赫数涡对的旋转角度存在显著的差异，这意味着以马赫数表征的流场可压缩性能够改变涡对旋转速度从而对融合过程产生一定的影响。此外，在涡对形态方面高马赫数涡旋在涡心处拉伸效应更明显，而低马赫数涡对涡量分布相对集中。

图5 不同马赫数涡对相互作用流场演化规律

3.2 不同马赫数涡对间距演化规律

为了更加深入地刻画可压缩性对涡相互作用流场的影响，计算了不同算例涡对间距随时间演化规律，如图6所示。在第1阶段中，涡对间距基本上保持不变，可以近似地认为涡对维持在相互围绕旋转的稳定状态，这也与涡量云图中直观获得的结论一致。在第2阶段中，涡对间距急剧减小，其相互靠近的速率可通过Biot-Savart诱导定律确定。随着两个涡旋之间距离的减小，自诱导产生对流效应对流场发展的主导地位逐渐削弱。随后涡对受无黏对流效应与黏性扩散效应竞争机制的影响，涡对间距出现振荡并且在黏性扩散的推动下完成最终的融合。比较不同马赫数涡对间距演化过程的差异发现：在相同无量纲时间下，低马赫数涡对间距较小，融合较为充分；换而言之，若将涡对从初始状态减小到相同无量纲间距，高马赫数涡旋所需的时间更长。可以认为可压缩性具有抑制涡相互作用发展的影响。类似现象在可压缩剪切层中引起了广泛的研究，并指出可压缩性起到维持流场稳定的作用[23]。值得注意的是，图中圆圈标注的数据为不可压缩涡相互作用的融合过程，可视作涡旋马赫数Ma趋向于0的极限理想情况，与低马赫数算例(可压缩性影响不明显)的模拟结果基本吻合。

图6 不同马赫数涡对间距随时间演化规律

3.3 不同马赫数涡对融合临界展弦比

在关于涡相互作用模型的理论研究中，确定系统开始融合的临界条件对于进一步认识涡相互作用物理过程及其规律奠定了基础。本文基于数值模拟结果，讨论可压缩性对于涡对临界展弦比的影响。不同马赫数涡对有效半径以及涡对间距随时间变化规律如图7所示：以无量纲涡对间距b/b0=0.9为临界标志[3](即相互作用第1、第2阶段的分界点)可以发现，随着马赫数的增加，涡对系统的临界展弦比变化不大，基本保持在理论推导获得的(a/b0)cr=0.24左右[7]。因而可以认为，以涡对展弦比描述的系统融合准则对于涡旋类型、涡旋雷诺数以及涡旋马赫数均具有较好的鲁棒性。然而，另一方面，相互作用第二阶段开始的临界无量纲时间随着马赫数的增加显著提高，这也从侧面印证了可压缩性具有推迟相互作用进程的作用。进一步地，为更深入地认识并预测可压缩涡相互作用发展的物理规律，本文下一节将针对不可压缩涡相互作用过程中的特征时间尺度，引入可压缩性修正，以统一不同马赫数涡对融合的进程。

图7 不同马赫数涡对有效半径及间距时间演化规律

4 相互作用时间尺度的可压缩性修正

在不可压缩涡相互作用模型中(Ma→0的极限情况)，流动特征时间定义为

(20)

根据上文结果可以发现，该特征时间难以对不同马赫数涡对相互作用过程进行归一，其原因是可压缩流动与低速流动的内在机制存在差异，而该特征时间无法体现出可压缩性强弱对于流场演化的影响。考虑到可压缩性具有推迟相互作用进程的影响，本节在不可压缩特征时间的定义中引入依赖于涡旋马赫数的可压缩时间尺度修正，为进一步分析可压缩涡相互作用的动力学行为提供一定的理论基础。首先，本文通过不同马赫数涡心处密度的时间历程从物理角度说明流场中可压缩性相对强弱的变化规律，如图8所示。其中涡心密度的时间变化率采用中心差分格式近似，即

(21)

式中：F为本文考虑随时间变化涡中心处的密度；Δt为时间步长。

图8 不同马赫数涡对涡心处无量纲密度和涡心处无量纲密度时间变化率的演化过程

涡心密度的时间变化率关于时间步长具有二阶精度。经过与高阶数值离散公式结果比较可以认为计算精度基本满足要求。

可以发现，不同马赫数涡对涡心处密度演化规律关于时间具有较好的统一性，其中不同马赫数涡心密度出现拐点的时间相互一致，如图8(b)所示。该结果表明，仅根据马赫数即可反映可压缩性的强弱而不依赖于流场具体演化过程的影响。因此在构造可压缩时间尺度修正时首先将马赫数视作给定常数而不考虑其与时间尺度之间的耦合作用。

关于可压缩修正项的具体表达形式，待定参数少且满足同类物理量纲相加原则的幂律模化(Power Law)在剪切层[24]、湍流[25]、稀薄气体流动[26]建模中应用广泛。其中涡相互作用模型大量存在于剪切层流动中可以认为内在符合相似的模化规律，然目前在可压缩问题中尚未推广。通过涡旋马赫数的幂律描述可压缩性强弱与流动特征时间的关系，可压缩时间尺度T表示为

(22)

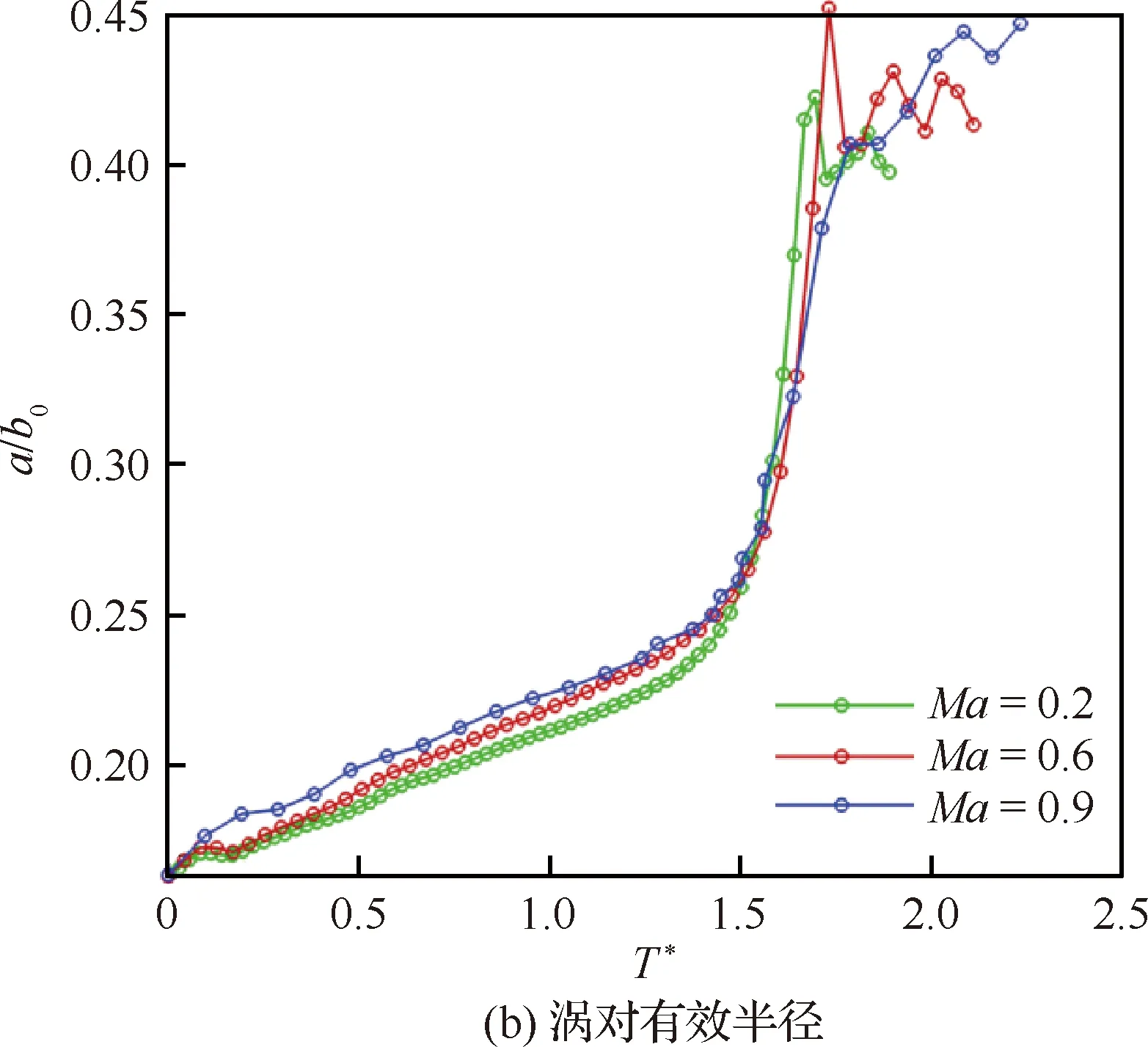
图9 通过引入可压缩时间尺度修正后统一的无量纲涡对间距以及涡对有效半径演化规律

5 结 论

针对流动可压缩性对涡相互作用动力学特征的影响这一科学问题，基于经过验证的Navier-Stokes算法以及压力泊松方程初始条件设置方法数值模拟了不同马赫数涡对相互作用流场演化过程，主要结论如下：

1) 可压缩与低速涡对相互作用流动结构与整体过程相似。另一方面，以高马赫数表征的可压缩性在提高涡量分布拉伸程度的同时具有抑制涡对系统融合，延迟相互作用进程的作用。

2) 以涡对展弦比描述的系统融合准则对流场可压缩性具有较强鲁棒性，然而临界无量纲时间随马赫数增加明显提高。

为在无量纲时间意义下统一不同马赫数涡对相互作用的进程，初步提出了可压缩时间尺度修正理论，其在不同涡旋雷诺数条件的适用性及其物理机制值得深入研究。

致 谢

感谢上海交通大学超算“π”为本研究提供的计算资源。