数学公开课教学评价模型

罗宇

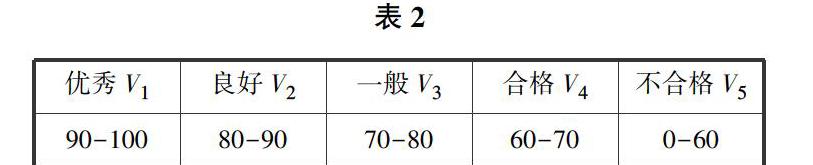
【摘要】本文基于层次分析法的模糊综合评价对数学公开课教学质量进行客观、定量的分析，并构建出数学公开课教学评定的模糊综合评价模型.通过具体教学案例验证了该方法的可行性，使数学公开课教学的评定结果更加准确公正，对教师教学水平的提升起到良好的导向作用.

【關键词】模糊综合评价法;数学公开课;教学质量评价;层次分析法

一、问题的提出

教师公开课教学[1]是中小学教师专业技能展示的重要形式.对教师的公开课教学进行准确的评价有利于激励教师不断进行教学内容和教学方法的摸索，反思自身教学方面的不足， 对提高课堂教学质量和教师基本功具有重要的作用，但是公开课教学涉及的要素较多， 评价指标受评价者知识水平、认知能力、感情色彩及个人偏好的直接影响，主观性较强，想要直接给出真实的教学评价成绩着实困难，即使部分评课教师也尝试着将评价指标定量化，但却依然缺少科学依据，评分结果也往往不尽如人意.因此对公开课教学进行综合评价是一个多层次的模糊综合评判问题.

对此，本文以我校数学公开课教学为例，探讨基于AHP的模糊综合评价法对某名教师的公开课教学成绩进行综合评分.

二、模糊综合评价法

模糊综合评价法（Fuzzy Comprehensive Evaluation）是由美国著名控制论学者、加利福尼亚大学L. A. Zadeh教授首先提出的[2]，特点是把集合中的隶属关系进行扩充，使得原本隶属度只能取0或1两个值推广至能取区间[0，1]中的任意数值，从而定量地刻画出模糊性对象，具体步骤如下：（1）确定被评价事物的影响因素集;（2）建立评语集;（3）确定权重集;（4）构造出模糊关系的综合矩阵R;（5）对因素子集Ui（i=1，2…，n）展开初级综合评价;（6）对U展开二级模糊综合评价;（7）综合评价模型的确定，并计算出模糊综合评价集;（8）依据最大隶属度原则，最大的bj所对应的等级（评语）Vj就是要求的最佳评判结果.

2.1 因素集的确立（构建数学公开课教学评定的指标体系）

本文在基于扬州市教育部已给出的评估体系基础之上，参考相关中小学教学比赛成绩评价细则和前人关于这方面的研究成果[3-4]，构建出了数学公开课教学评价模型，如表1.

【参考文献】

[1]丁家玲，叶金华.层次分析法和模糊综合评判在教师课堂教学质量评价中的应用[J].武汉大学学报（哲学社会科学版），2003（02）：241-245.

[2]陈水利，李敬功，王向公.模糊集理论及其应用[M].北京：科学出版社，2008.

[3]孙晓玲，王宁，梁艳.应用BP 神经网络的教学评价模型及仿真[J].计算机仿真，2010（11） ： 314-318.

[4]张金梅，员世芬，谢克明.人工神经网络在教学质量评价体系中的应用[J].太原理工大学学报，2005（01）：37-39.

[5]许树柏.层次分析法原理[M].天津：天津大学出版社，1988.

[6]Cecilia K.Y，Chan，Lillian Y.Y.Luk， Min Zeng.Teachersperceptions of student evaluations of teaching[J]. Educational Research and Evaluation， 2014（04）：275-289.