人教版“数学广角”与青岛版“智慧广场”习题综合难度比较研究

张柱 马晓霜

【摘要】根据鲍建生提出的习题综合难度模型，结合小学数学教材的实际特点，对每个难度因素水平进行调整.根据调整后的模型对人教版“数学广角”与青岛版“智慧广场”习题进行对比分析.发现“数学广角”与“智慧广场”在背景、数学认知、知识综合方面无明显差异，在运算方面，“智慧广场”习题难度高于“数学广角”，在推理方面，“数学广角”习题难度高于“智慧广场”.

【关键词】小学数学教材;数学广角;智慧广场;习题难度

一、前言

《义务教育数学课程标准》指出：“让学生通过学习获得适应未来社会生活和进一步发展所必须的数学的基础知识、基本技能、基本思想、基本活动经验.”“数学广角”和“智慧广场”分别是人教版和青岛版小学数学教科书的重要组成部分，它们作为体现数学思想的主要阵地，在培养学生的核心素養方面具有举足轻重的作用.两者都以单元的形式独立呈现，旨在培养学生的数学思想，激发学生的数学思维，提高学生解决数学问题的能力.

二、研究对象与研究方法

1.研究对象

选取人教版“数学广角”和青岛版“智慧广场”习题作为研究对象.“数学广角”出现在人教版教材二年级至六年级的最后一单元.青岛版教材一年级至三年级每册均设置了两个“智慧广场”单元，且它们相继出现在每册教材的中间和末尾部分，四年级至六年级每册教材都设置了一个“智慧广场”单元，且位于每册教材的末尾.“数学广角”和“智慧广场”都设有独立的习题供学生练习和探究.这里的习题是指“数学广角”的课后练习题和“智慧广场”的“自主练习”部分，不包括“做一做”部分.在统计计数时，均按第一层级序号计数.经过统计，“数学广角”课后练习题一共72道，“智慧广场”课后练习题一共87道.

2.研究方法

鲍建生（2002）在Nohara（2001）提出的总体难度（Overall difficulty）概念的基础上，结合我国数学课程的实际情况建立了数学课程综合难度模型.我国许多学者在该模型的基础上进行了大量的研究.比如：王建磐，鲍建生（2014）对比分析了包括中国在内的六个国家高中数学教材例题;卢建川，廖运章，王华娇（2015）分析了英国数学英才选拔考试MAT综合难度;濮安山，徐慧敏（2016）对比分析了PEP（A）版与IBID版数学教材中平面向量例题难度;汪飞飞，杨静（2017）比较了大陆与台湾高中数学教材例题难度.本研究在前人的基础上，结合小学数学练习题的特点，对综合难度模型进行改进，使之更加符合小学数学练习题的现状.

根据上表，对每一个难度因素水平进行等级变量自然赋值（从低到高依次按照自然数1，2，…进行赋值），并根据下面的公式计算出每一个难度因素的加权平均值.

其中，di表示第i个难度因素的加权平均值，dij表示第i个难度因素的第j个水平的权重，nij表示“数学广角”和“智慧广场”习题中属于第i个难度因素的第j个水平的题目的个数，n代表样本总数（“数学广角”习题总数或者“智慧广场”习题总数）.

三、研究结果与分析

根据表中统计的结果，下面首先利用折线图对比分析“数学广角”和“智慧广场”习题在“背景”“数学认知”“运算”“推理”“知识综合”这五个难度因素上的差异，然后利用雷达图对“数学广角”和“智慧广场”的习题综合难度做出比较.

1.研究结果

（1）背景因素

图1表明：“数学广角”和“智慧广场”在背景因素方面表现出一致性，无明显差异，在无实际背景水平上，“智慧广场”略高于“数学广角”;在生活背景和其他背景水平上，“数学广角”均略高于“智慧广场”.总体来看，“数学广角”和“智慧广场”习题所占比例最高的是生活背景，大约为70%，其次是无实际背景，最后是其他背景.

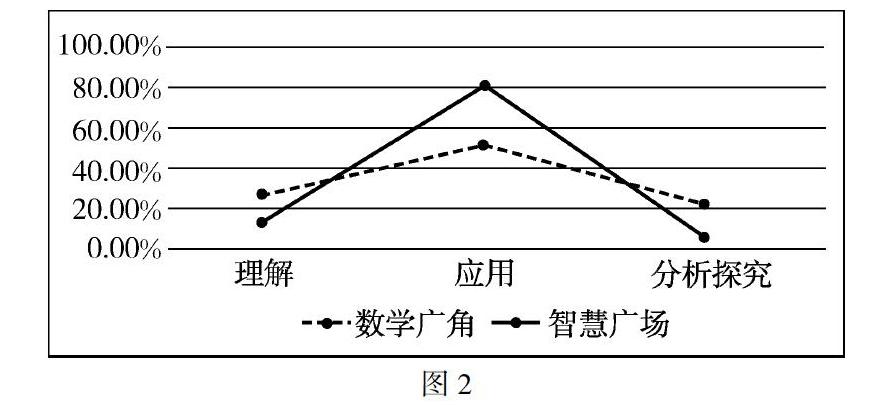
（2）数学认知因素

由图2可知：“数学广角”和“智慧广场”部分的习题在数学认知因素上表现出较大的差异，在理解和分析探究水平上，“数学广角”高于“智慧广场”接近十五个百分点;在应用水平上，“智慧广场”的习题所占比例高达80%，“数学广角”的习题所占比例约为51.4%，两者相差近30%.

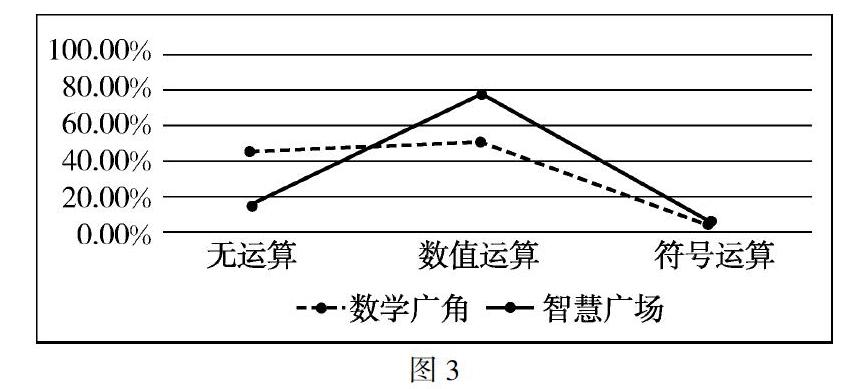
（3）运算因素

由图3可知：“数学广角”和“智慧广场”的习题在运算因素上差异较大，在无运算水平上，“数学广角”习题所占比例较大，约为45.8%，“智慧广场”习题所占比例较小，约为16.1%;在数值运算水平上，“智慧广场”习题所占比例较大，约为77%，“数学广角”习题所占比例约为50%;在符号运算水平上，“数学广角”和“智慧广场”习题基本保持一致，且所占比例只有5%左右.

（4）推理因素

在无推理水平和简单推理水平上，“智慧广场”要高于“数学广角”;在复杂推理水平上，“数学广角”要高于“智慧广场”.总体来看，所占比例最高的是简单推理水平，均在50%以上，其次是无推理水平，最后是复杂推理水平.

（5）知识综合因素

“数学广角”和“智慧广场”习题在知识综合因素上表现出高度的一致性，两者无明显差异.“数学广角”和“智慧广场”习题90%左右只涉及一个知识点，只有10%左右的习题涉及两个知识点.

2.分析

根据“数学广角”和“智慧广场”习题在“背景”“数学认知”“运算”“推理”“知识综合”这五个难度因素上的加权平均值，利用数据绘制出“数学广角”和“智慧广场”习题综合难度雷达图.

“数学广角”和“智慧广场”习题难度在“背景”“数学认知”“知识综合”这三个因素上无明显差别，在运算因素上，“智慧广场”高于“数学广角”，在推理因素上，“数学广角”高于“智慧广场”.总体来看，两个五边形没有保持平衡.

四、结论与建议

1.结论

从“背景”“数学认知”“运算”“推理”“知识综合”五个因素对“数学广角”和“智慧广场”习题综合难度进行对比分析，得出如下结论：

（1）在背景因素方面，两个栏目的习题都大多采用以生活情境的形式展开，其他背景所占比例太小.涉及数学史和数学文化背景的习题太少.

（2）在数学认知因素方面，两个栏目的习题在应用水平上所占比例太大，尤其是“智慧广场”所占比例高达80%，而分析探究水平所占比例较小.

（3）在运算因素方面，“智慧广场”习题过于重视数值运算，在数值运算水平上所占比例达到77%.

（4）在推理因素方面，两个栏目的习题大多集中在无推理和简单推理水平上，而复杂推理水平所占比例较小.

（5）在知识综合因素方面，两个栏目的习题90%左右只涉及了一个知识点，没有加强各个知识点之间的融合.

在综合难度方面，两个五边形没有保持平衡，在“背景”“数学认知”“知识综合”方面基本保持一致，在运算方面，“智慧广场”习题难度更高，而在推理方面，“数学广角”习题难度更高.

2.建议

（1）习题背景应该将生活背景与其他背景相结合

目前，“数学广角”和“智慧广场”习题以生活背景为主，包括个人生活和社会生活，“数学广角”和“智慧广场”作为渗透数学思想、开阔学生视野的栏目，在习题编写过程中应该考虑多围绕数学文化、数学史和其他学科背景展开，做到将生活背景与其他背景相结合.

（2）习题应该多引导学生经历分析和探究的过程

《义务教育数学课程标准》指出：“数学教学活动应激发学生兴趣，调动学生积极性，引发学生的数学思考，鼓励学生的创造性思维.”在习题编写方面应该多设置探究性问题，引发学生积极思考，分析问题，解决问题.

（3）习题应该加强各个知识点的融合

《义务教育数学课程标准》将小学数学内容分为“数与代数”“图形与几何”“统计与概率”“综合与实践”四大版块，每个版块都有各自的知识点，知识点之间不是相互独立和割裂的，而是密切联系、相互交融的.在习题编写时应该涉及多个知识点，以小问题的形式编写.这样有助于提高学生的灵活运用能力.

【参考文献】

[1]中华人民共和国教育部.义务教育数学课程标准（2011年版）[M].北京：北京师范大学出版社，2012.

[2]叶健，李文文.“核心素养”背景下数学广角课堂教学现状调查及策略研究[J].课程教育研究，2017（04）：117.

[3]贾先飞.人教版小学新旧教材“数学广角”的对比分析[J].亚太教育，2015（13）：21.

[4]鲍建生.中英两国初中数学期望课程综合难度的比较[J].全球教育展望，2002（09）：48-52.

[5]王建磐，鮑建生.高中数学教材中例题的综合难度的国际比较[J].全球教育展望，2014，43（08）：101-110.

[6]卢建川，廖运章，王华娇.英国数学英才选拔考试MAT综合难度分析[J].数学教育学报，2015，24（06）：31-34.

[7]濮安山，徐慧敏.PEP（A）版与IBID版数学教材中平面向量例题难度的比较[J].数学教育学报，2016，25（03）：10-13.

[8]汪飞飞，杨静.大陆与台湾高中数学教材例题难度比较：以“指数和对数函数”为例[J].课程教学研究，2017（04）：38-43+47.