实验:初中生数学思考力增长的新作用点
陈兆绪


【摘要】数学思考力是指一种逻辑运用、本质联系和信息建立的能力,也是一种搜索更广、潜入更深的思维活动.以数学问题为导向,以解决问题为目标,注重学生对知识的探究过程,这正是数学思考力的体现.以数学实验为载体,让学生在动手操作过程中,掌握思考方法,懂得思考步骤,具备思考能力,促进学生思考力的增长.
【关键词】初中数学;数学实验;数学思考力
德国数学家康托尔说过:“数学的本质在于思考的充分自由.”义务教育课程标准将“双基”调整为“四基”,即在“基础知识、基本技能”的基础上,增加了“基本思想、基本活动经验”.数学思考力是数学核心素养的内核.数学实验可以启迪学生的思维,在课堂中以学生为中心,以实验为手段,使学生在数学实验操作过程中理清数学本质,并让数学思考意识在数学教学中落地生根.
一、数学实验与学习方法:让学生在实验中形成主动思考意识
美国心理学家布鲁纳曾说:“兴趣是对学习的最好刺激,一个人抱着兴趣去研究某个问题时就会达到惊人的程度.”数学实验要求学生用亲身观察、思考和试验等途径实现知识内化,同时,在实验中设置一连串层层深入的问题,可以激发学生学习兴趣,引领着学生兴趣盎然的走向挑战,从而促使学生在实验中形成主动思考意识.
案例1 一元一次方程应用
演示实验:用个大水杯向一个小水杯倒水.
由于杯子容量不一样,所以,在大杯往小杯倒水后,会发生水面高度的变化,利用这一生活中比较常见的事例,创设教学情境,让学生对水面高度的变化原因产生好奇,为后面的数学实验做好铺垫.
为学生提供两个底面直径分别为3.2 cm的A量筒和4 cm的B量筒.让学生首先将B量筒装满水,水面高度为4 cm,然后将B量筒内的水倒进A量筒内,认真观察倒水前后两个量筒内水的高度有什么变化?A量筒内的水面高度为多少?
在兴趣的驱动下,学生积极地开始动手实验,这种直观的、简单的实验操作让学生很快就发现了在倒水的过程中,由于底面半径发生了变化,所以,水面的高度也随之发生变化,但始终存在水的体积不变这一现象.根据这一等量关系,我们可以假设A量筒内的水面高度是x cm,则有:
选择学生比较熟悉的体积问题,其等量关系一目了然,学生通过等体积水及水面的变化过程产生问题意识,并体会其中所蕴含的不变量,从而引出用一元一次方程求解实际问题的基本步骤.
二、数学实验与数学理解:让学生在实验中思考数学概念的内涵和外延
心理认知学认为:初中生的思维能力比较弱,且正处于想象、推理的萌芽阶段.处于该阶段的学生思考力的形成离不开直观形象支撑,尤其是对于数学概念的理解,运用数学实验可帮助学生直观地观察数学对象,让学生不再抽象中挣扎徘徊,在实验中思考数学概念的内涵与外延,加深对数学概念的理解.
师:现在请同学们将一张纸平放在桌面上,然后往纸上滴一滴墨水,然后将纸张对折压平,稍等片刻后,打开纸,观察有什么现象?
学生实验,很快有的学生就发现纸张两边的墨迹沿着折痕折叠后重合.继续出示图1.
师:谁能说出如何剪出这幅图案呢?请你们动手试一试.
(学生动手操作,发现将图案对折后两部分完全重合,所以可以利用图形对称的方法剪出图案.)
师:通过前面两次操作,你们发现它们有什么共同点?
生1:像这样,将一个图形沿着一条直线翻折过去,如果翻折后的两个图形关于这条折痕重合,就可以说这两个图形关于折痕对称.
生2:在数学上,我们可以称这两个图形是轴对称图形,这条直线是对称轴.
师:那我们学过的哪些图形是轴对称图形?
生3:圆形、等边三角形.
生4:长方形.
生5:平行四边形.
生6:平行四边形好像不是轴对称图形.
学生出现了不同的意见,有的赞同,有的反对,如何来验证呢?接下来笔者让学生用学具进行自主操作.
生7:我从平行四边形的一个角点向其对边垂直剪下一个三角形,然后将这个直角三角形拼在另一个缺口,就变成了长方形.因为长方形是轴对称图形,所以平行四边形也是.
师:听着好像有道理.
生8:可是我发现无论怎么折,两边都无法重合,所以我认为平行四边形不是轴对称图形.
师:还有补充的吗?
生9:刚才我们学过判断一个图形是否为轴对称图形,关键是看它对折后两边是否能重合.所以,依照轴对称图形的概念来看,显然平行四边形不是轴对称图形.
在对称轴与轴对称图形概念的教学中,笔者安排了三次数学实验,让学生在环环相扣的实验中充分地思考、体验、感受,以及产生不同觀点之后的相互碰撞、辩论,有效激活了学生的思考力.
三、数学实验与动态生成,让学生在实验中思考“变”与“不变”
数学实验是学生通过动手、动脑和动口“做数学”的一种学习活动,是学生综合运用作图工具、测量工具、模型、剪刀和纸张等进行数学思维的探究活动.克莱因曾说过:“数学是一种精神,一种理性精神.”其中,“理性”二字充分体现从“变”中准确把握“不变”的本质,并能以“不变”应“万变”.
问题1:已知在△ABC中,边长BC、AC、AB的长度分别为a、b、c.
(1)若△ABC为一般三角形时,a、b、c之间有什么数量关系?
(2)若∠B=∠C,a、b、c之间有什么数量关系?
(3)若∠A=∠B=∠C,a、b、c之间有什么数量关系?
请同学们在草稿纸上画图进行探索,从问题(1)到问题(3),从一般到特殊,让学生认识到当三角形的角度发生变化时,其对应三边关系也随之发生变化.
预设生成:学生从问题(1)中得到a-b
这是笔者在课前没有预设到的,所以,趁着学生兴趣正浓厚时,让学生利用表格、几何画板等工具自主设计实验,学生通过多组数据的统计分析,结果发现当测定的数值保留精度足够高,几乎所有的数值都满足a2+b2=c2.由此,我们就可以说直角三角形的两条直角边的平方和等于斜边的平方,即勾股定理.
在数学学习过程中,常常遇到学生因找不到突破口而困惑的现象,此时可通过数学实验来发现规律,打开突破口解决问题.在上述环节中,我们以特殊值获得了关系式a2+b2=c2,那么该公式是否具有普适性?需要学生再次从特殊回到一般,这也是学生
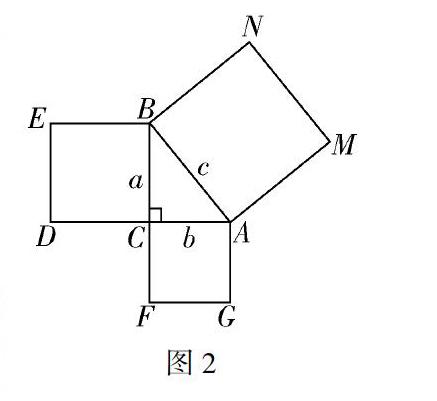
思考力增长的难点.通过分析式子结构关系,可以联想到边长分别为a、b和c的正方形面积,因此,应用“构造法”的思想,对任意的直角三角形ABC进行构造,如图2所示.
只要证明正方形DCBE和CFGA的面积之和等于正方形BAMN的面积即可.我们常用的方法是用割补法,这一过程,对于学生的思维具有极大的挑战.只有给予学生充足的时间,鼓励学生积极思维,勇敢面对挑战,才能克服思维的障碍.学生在草稿纸上作出了多种尝试:
生3:我首先对a2+b2=c2进行变形,得到(a-b)2+2ab=c2,所以构造出图3.然后根据割补法得到图4.
利用数学实验将整个勾股定理的探索过程有机串联起来,让学生在边操作边思维的过程中实现对勾股定理的猜测、推断和证明,最后反思和总结勾股定理的证明过程,将知识上升为经验,促进学生思考力再次增长.
英国迪士尼乐园的路径是游客“走”出来的,数学思考力的构建也需要依靠师生的共同努力才能形成.在数学实验教学中,应给学生预留充足的时间,激活思考点,延展数学思考触角,让数学思维逐渐走向开放,形成勤于思考的良好习惯.
【参考文献】
[1]李宾, 张徐慧. 例谈数学思考力[J]. 中学数学, 2018(20):49-51.
[2]杨友平. 数学思考力:在“自然境遇”中自由生长[J]. 江苏教育研究, 2015(10):62-65.

