最大度为3的图的L(2,1)-边标号的有效算法

叶 林 李 涌

(台州第一技师学院,浙江 台州 317500)

1 基础知识

图G的一个L(2,1)-标号问题来自于无线电的频率分配问题[1-2].本文中G的点集和边集分别用V(G)和E(G)表示.对任意的v∈V(G),用d(v)表示G中点v的度数；对任意的x,y∈V(G),d(x,y)表示点x,y之间的距离.对任意的e1,e2∈E(G),d(e1,e2)表示边e1,e2之间的距离.

令f:V(G)→{0,1,2,3,…}为一个映射,若对任意的x,y∈V(G),满足当d(x,y)=1时,有|f(x)-f(y)|≥2.当d(x,y)=2时,|f(x)-f(y)|≥1,则称f为G的一个L(2,1)-标号.图G的L(2,1)-标号数λ(G)是指最小的正整数k使得G有一个L(2,1)-标号f满足f(V)⊆{0,1,2,…k}.Griggs和Yeh[2]证明了对最大度Δ≥1的图G有λ(G)≤Δ2+2Δ. 此外, 他们还猜想对于任何Δ(G)≥2的图,有λ(G)≤Δ2.并证明对于一些特殊图,如路,2,树以及直径为2的图时,该猜想成立.关于这类问题的研究,参考文献[2-4].

类似地,给定图G的一个L(2,1)-边标号是从图G的边集到非负整数集的一个映射f满足：对任意的e1,e2∈E(G),满足当d(e1,e2)=1时,|f(e1)-f(e2)|≥2;当d(e1,e2)=2时, 有|f(e1)-f(e2)|≥1.

图的L(2,1)-边标号数λ’(G).显然，对图G的边标号研究相当于对于对其线图L(G)的点标号研究.近年来,L(2,1)-边标号问题也被广泛地研究[5-19].

本文主要研究Δ(G)=3的简单图G,本文给出一个算法,可以在线性时间内给出图G的16-L(2,1)-边标号,从而证明λ’(G)≤16,验证Griggs和Yeh猜想对于该类图成立.

2 图的分解

定理1[20]设G是一个最大度为3的简单图,则G能被分解成2个边不交的子集C和F.其中C表示点不交的圈集,F表示最大度不超过3的森林.

为了文章叙述简洁，定义一下概念和符号.我们称F的一条边e是圈关联边,如果e与C内的一个圈关联.如果一个圈C的两条圈关联边e,f满足dG∪e∪f(e,f)=2,则我们称e是f的圈间隔边.记I(e)表示e的圈间隔边集.我们称一条边e是单边,如果e连接着C内的两个圈.为了方便起见,记N(e)表示边e的邻边集,l(e)表示边e的标号.记l(A)表示边集A的标号集.

令E1={e|e是一条圈关联边,存在另一条圈关联边f与e相邻}.

令E2是所有不属于E1的圈关联边组成的集合.

令E3=F-E1-E2.

令A={0,1,2,3,4},B={8,9,…15,16}.我们称数a∈C是边e的最小有效数,如果a是用于标号e的数集C中满足正常L(2,1)-边-标号的最小数.

2.1 标号算法

2.1.1 标E1的边

算法E1

步骤1 若存在三条未标号的两两相邻边e,f,g∈E1.分别取A中的最小有效数a,b标给e,f,g中的两条边,使得能被a,b正常标号的边优先标号.取{4,5,6}中的最小有效数标给余下的边.

步骤2 若存在两对未标号邻边e,f∈E1和g,h∈E1.满足e,f和g,h分别与一条边的两端点相关联.分别取{0,1,2,3}中的最小有效数a,标给e,f和g,h中的各一条边,使得能被a,b正常标号的边优先标号.取{3,4,,6}中的最小有效数标给余下的两条边.

步骤3 若存在一对未标号邻边e,f∈E1.分别取A中的最小有效数a,b标给e,f,使得能被a正常标号的边优先标号,满足(a,b)≠(1,4).

定理2 算法E1能在线性时间内用A∪{5,6}内的数对E1进行正常的L(2,1)-边标号.

证明:设e,f,g是步骤1所述三条未标号边.不失一般性,设边e满足0∉l(I(e))，则e能被标为0.2∉l(I(f))(同理可得g,同),则f能被标为2,{4,5,6}中至少有1个数可以标给g.若不然,则考虑标号3,若3∉l(I(f)),则f能被标为3.{5,6}中至少有1个数可以标给g.若l(I(f))={2,3}.则f能被标为4,g能被标为6.同理可得0∈l(I(e))的情况.

设e,f和g,h是步骤2所述两对未标号边.易见,d(e,f)=1,不失一般性,设边e满足0∉l(I(e))(同理可得f,g,h,同),若边g满足1∉l(I(g))(同理可得h,同),则e能被标为0,能被标为1.则{3,4,5,6}中至少有2个数可以标给f,h.若不然,则考虑标号2,若2∉l(I(g)),则g能被标为2.{3,4,5,6}中至少有2个数可以标给f,h.若l(I(g))={1,2},则可将g标为3.{4,5,6}中至少有2个数可以标给f,h.同理可得0∈l(I(e))的情况.

设e,f是步骤3所述一对未标号边.不失一般性,设边e满足0∉l(I(e)),则e能被标为0.{2,3,4}中至少有1个数可以标给f.若l(I(e)),l(I(f))不同时为{0,1}或{0,3}.则e,f能被{1,3}标号.若不然,则e,f能被{2,4}标号.

易见,算法E1需要运行0(E1)个时间单位.证明完毕.

2.1.2 标E2的边

算法E2

步骤1 若存在一条未标号边e是一条弦或者单边,则取A中的最小有效数标给e.

步骤2 若存在一条未标号边f∈E2,则取A∪{5,6}中的最小有效数标给f.

定理3 算法E2能在线性时间内用A∪{5,6}内的数对E2进行正常的L(2,1)-边标号.

证明:设e是步骤1所述的一条未标号边.易见I(e)≤4,因此e至多需要避免A中的4个标号,则A中至少还有1个标号可以标给e.

设f是步骤2所述的一条未标号边.此f至多与一对非圈关联边g,h相邻. 易见,g,h未标号,且任何一条边至多与E1内一对已标号邻边相邻, 因此,f至多需要避免4个标号. 由于I(f)≤2,因此f至多需要避免A∪{5,6}中的6个标号,至少还有1个标号可以给f.

易见,算法E2需要运行0(E2)个时间单位.证明完毕.

引理1 设e是一条圈关联边.若e的圈间隔边是弦或者单边,则执行算法E1,E2后,e不会被标为6.

2.1.3 标C的边

为了方便起见,我们称单边e是未标号圈Ci的一条感染边,如果e连接着Ci和一个已标号圈Cj.

令C1= {Ci|存在Ci的一条边,不与任何弦或感染边相邻}

令C2= {Ci|存在Ci的一条边,仅与一条弦或感染边相邻,Ci∉C1}

令C3=C-C1-C2

算法C

步骤1 若存在一个未标号圈Ci∈C1,e1∈Ci是不与任何弦或感染边相邻的边.一定的方向,记e1,e2,…,ei表示Ci的所有边.取B中的最小有效数依次标号e(2≤t≤i),e.

步骤2 若存在一个未标号圈Ci∈C2,记e1∈Ci是仅与一条弦或感染边e相邻的边.记e2是e的另一邻边.以一定的方向,记e1,e2,…,ei表示Ci的所有边.

(1)若e2的非e相邻圈关联边不是感染边.取{7,8}中的最小有效数标给e2,取B中的最小有效数依次标号et(2≤t≤i),e1.

(2)若e2的非e相邻圈关联边是感染边.将e2标为6,取B中的最小有效数依次标号et(2≤t≤i),e1.

步骤3 若存在一个未标号圈Ci∈C3.

(1)若存在Ci上的两条连续感染边或弦e,f,满足{7,8}⊄l(N(e))l(N(f)),记e1是e和f都相邻的圈边.以一定的方向,记e1,e2,…,ei表示Ci的所有边.取{7,8}中的最小有效数标给e1，将e3标为6.取B中的最小有效数依次标号ei-t(0≤t≤i-4),e2.

(2)若对于Ci上的任何两条连续感染边或弦e,f,足{7,8}⊆l(N(e))∪l(N(f)).Ci的任何一条边为e1,以一定的方向,记e1,e2,…,ei表示Ci的所有边.将e1标为6,取B中的最小有效数依次标号et(2≤t≤i).

定理4 算法C能在线性时间内用B∪{6,7}内的数对C进行正常的L(2,1)-边标号.

证明:设Ci是C1内的一个未标号圈.考虑到C的边et(2≤t≤i)至多与两条圈关联边e,f相邻.由于e,f可能是弦或感染边.则et至多需要避免由l(et-1),l(et-2)引起的4个标号,以及由l(N(e)),l(N(f))引起的4个标号.因此,至少还有|B|-4-4=1个数可以标给et.考虑到e1至多需要避免由l(ei),l(e2),(ei-1)和l(e3)引起的8个标号.则至少有|B|-8=1个数可以标给e1.

设C是步骤2.1中所述C2内的一个未标号圈.由于e3一定与感染边或弦相邻,根据引理1,与e2相邻的圈关联边,不会被标为6.因为{7,8}≠l(N(e)),所以{7,8}中至少有一个数可以标给e2.考虑Ci的边et(3≤t≤i-1),至少有|B|-4-4=1个数可以标给et,2个数标给ei.考虑到e1至多需要避免由l(ei-1),l(ei-2)和l(e3)引起5个标号,以及l(N(e))和l(e2)引起的3个标号,则至少还有1个数可以标给e1.

设Ci是步骤2.2中所述C2内的一个未标号圈.易见,单边或弦的标号由A给出.若与e2相邻的圈关联边是弦,e2能被标为6.假设e是感染边,设Cj是异于Ci的与e相连的圈.易见,在标号Cj时,Ci未被标号,则e不是Cj的感染边,6∉l(N(e)).因此,e2相邻的圈关联边是感染边或弦时,e2能被标为6.对于Ci的边et(3≤t≤i-1),至少有|B|-4-4=1个数可以标给et,3个数可以标给ei,2个数可以标给e1.

设Ci是步骤3.1中所述C3内的一个未标号圈.见{7,8}中至少有一个数可以标给e1.由于e3与两条感染边或弦相邻,e3能被标为6.此,至少还有|B|-4-4=1个数可以标给ei-t(0≤t≤i-4).考虑e2至多需要避免l(ei),l(e4)引起2个标号,l(e1)引起的2个标号,以及感染边引起的4个标号,至少还有1个数可以标给e2.

设Ci是步骤3.2中所述C3内的一个未标号圈. 易见,e1能被标为6. 至少有|B|-4-3=2个数可以标给et(2≤t≤i), 考虑ei至多需要避免l(ei-1),l(ei-2)和l(e2)引起的5个标号,及感染边引起的3个标号,则至少还有1个数可以标给ei.

易见,算法C需要运行0(C)个时间单位,即能在线性时间内用B∪{6,7}内的数对C进行正常的L(2,1)-边标号.证明完毕.

2.1.4 标E3的边

易见,森林F可以由一系列的树T1,T2,T3…Tn组成,其中Ti∩Tj=φ,1≤i,j≤n,i≠j.

为方便起见,我们称E3⊂F内的边e是特殊边,如果e与圈关联边相邻.

令E32={e|e是一条特殊边,且e∉E31}

算法E3

步骤1 对任意的一棵树T∈F,定T内任意一个叶子点v作为根点, 设边e=xy∈T, 则记d(v,e)=min{d(v,x),d(v,y)}表示v与e的距离.

步骤2 以根点v∈T的距离由近到远,若存在一对特殊边e,e′,满足d(v,e)=d(v,e),取{5,6}中的最小有效数优先标号e,e′中相邻较多圈关联边的边(若不能被5正常标号,则考虑邻边),若不能正常标号,则不进行.

记e,e′是距离v最远的一对特殊边,ei-1是距离ei最近的标号特殊边.

(1)若d(ei-1,ei)=2,l(ei-1)=6

(2)若d(i-1,ei)>2,且存在一条与v更近,与ei距离为2的圈关联边.

(3)若不存在一条与v更近,且与ei距离为2的圈关联边.

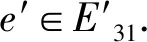
(2)若e′∈E31与两条圈关联边相邻.记与e,e′相邻的圈关联边为f.若l(f)=5,记e′的非f圈关联邻边为f′.取消f,f′标号.取A∪{5}中的最小有效数依次标号f,f′.

(3)若e′∈E32, 存在e′的邻边ei是特殊边, 且l(ei)=6.则取消ei标号,将e′标为6.

(4)若e′∈E32,e′未被标为5或6,将e标为6.

步骤4 以根点v∈T的距离由近到远,取B∪{6,7}中的最小有效数依次标给T内未标号边,且满足与v距离相同的一对邻边,特殊边(相邻较多圈关联边)优先被标号.

定理5 算法E3能在线性时间内用{0,1,…,15,16}内的数对E3进行正常的L(2,1)-边标号.

设T是步骤5中所述一棵未完全标号树.对T进行归纳假设. 当T=1时, 可以由B∪{6,7}内的数标号.假设T=k-1时,B∪{6,7}能对T内未标号边进行正常L(2,1)-边标号.证明当T=k时,结论也成立.设e∈T是离v最远的一条未标号边.根据归纳假设,T-e的未标号边能被B∪{6,7}正常的L(2,1)-边标号.考虑e的可能情况:

情况1 若e不是特殊边.则e至多需要避免由l(N(e))引起的6个标号,离根点v较近的,与e距离为2的两条边的2个标号.因此至少有|B|+2-6-2=3个数可以标给e.

情况2 若e是特殊边,且e∈E31.

(1)若e与4条圈关联边相邻.易见,e至多需要避免距离为2的8条圈边的8个标号,圈关联边的可能标号6,则至少有|B|-8=1个数可以标给e.

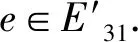
(2-1)若e′如步骤3.1所述,当e′被{0,2,4}中的数标号,则B中至少有|B|-6=3个数可以标给e. 当e′未被{0,2,4}标号, 则e至多需要避免l(e′)引起的3个标号,距离为2的6条圈边的6个标号, 圈关联边的可能标号5,B∪{7}至少有|B|+1-6-3=1个数可以标给e.

(2-2)若e′如步骤3.2所述,则e至多需要避免l(e′)引起的3个标号,距离为2的7条边的7个标号,B∪{6,7}至少有|B|+2-3-7=1个数可以标给e.

(2-3)若e′是已标号的特殊边,则l(e′)≤6.则B至少有|B|-2-6=1个数可以标给e.

(3)若e与两条圈关联边相邻.易见,e至多需要避免离根点v更近的邻边引起的3个标号,距离为2的6条边的6个标号,圈关联边的可能标号5,B∪{7}至少有|B|+1-6-3=1个数可以标给e.

情况3 若e是特殊边,且e∈E32.记e的一条邻边为e′,满足d(v,e)=d(v,e′).(若不存在e′,易见B∪{7}中至少有1个数可以标给e.)

(1)若e与两条圈关联边相邻.

(1-1)若l(e′)≤5,则e至多需要避免离根点v更近的邻边引起的3个标号,距离为2的6条边的6个标号,B∪{7}中至少有|B|+1-6-3=1个数可以标给e.

(1-2)若l(e′)=6.若存在一条标号特殊边f,满足l(f)=5,d(e,f)=2,则B中至少有|B|-3-4=2个数可以标给e.若不存在,则根据步骤2.2.2,B中至少有|B|-4-4=1个数可以标给e.

(2)若e与一条圈关联边相邻.

(2-1)若l(e′)≤6,B中至少有|B|-5-2=2个数可以标给e.

(2-2)若l(e′)>6,根据步骤2.1.1,e至多需要避免邻边引起的6个标号,距离为2的2条边的2个标号,B中至少有|B|-6-2=1个数可以标给e.

由此可得,T的边能被B∪{6,7}正常标号,归纳假设成立.

显然,该标号过程需要0(|E3|)的时间.从而对图G的所有边进行标号需要0(|E(G)|)的时间.

如上所述,我们能在线性时间内用{0,1,…,15,16}对G的边进行标号.且对于满足Δ(G)=3的简单图G,有λ’(G)≤16,Griggs和Yeh猜想成立.