基于标定板的协作机器人Denavit-Hartenberg参数标定研究*
□ 刘瑞超 □ 张 波
上海交通大学 机械与动力工程学院 上海 200240
1 研究背景

在主流的辨识方法中,需要使用激光测量仪和视觉传感器等进行标定,这样做的缺点是所需设备昂贵,操作复杂[1-3]。
笔者以微分运动的思路,优化运动学误差模型的计算方法,并通过仿真验证这一方法的有效性。与此同时,笔者针对协作机器人的特点,提出一种基于标定板的协作机器人DH参数标定方法,设备简单,通用性强,方法简便。通过模型仿真和试验,验证了这一标定方法的可行性和可操作性[4-5]。
2 运动学误差模型及算法优化
笔者研究的机器人为上海交通大学机器人研究所研发的六自由度协作机器人。使用DH参数法对协作机器人进行建模,协作机器人各连杆坐标系如图1所示。其中,基座坐标系三个坐标方向为X0、Y0、Z0。协作机器人模型DH参数见表1,其中,αi为相邻关节轴夹角,ai为连杆长度,di为连杆偏距,θi为关节转角,i为连杆编号,i=1,2,3,…,6。
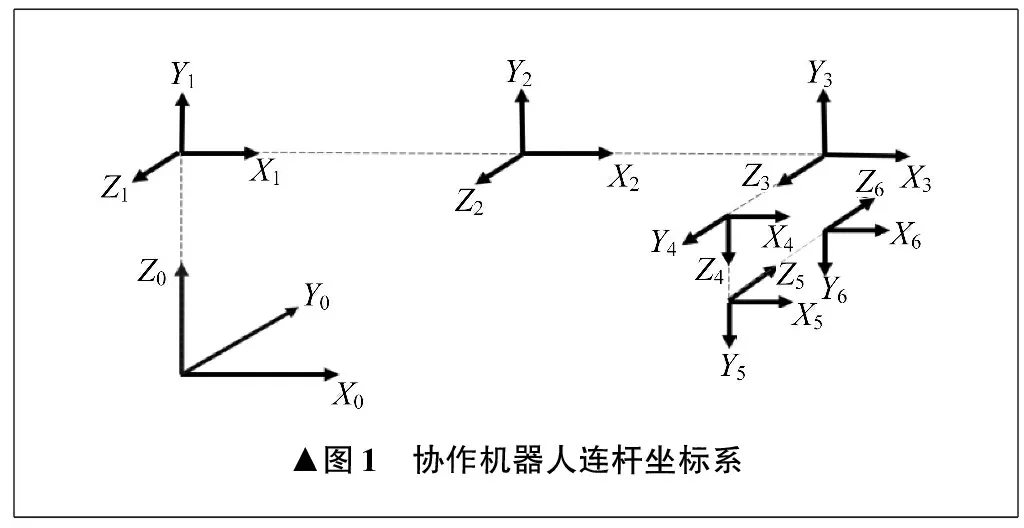
▲图1 协作机器人连杆坐标系
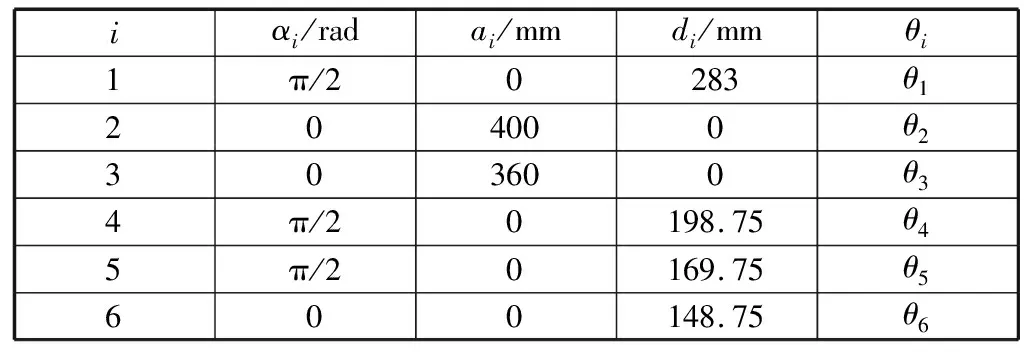
表1 协作机器人模型DH参数
根据文献[2]中的经典机器人DH参数法,得到连杆i坐标系相对于连杆i-1坐标系的齐次变换矩阵i-1Ti。协作机器人末端坐标系相对于基座坐标系的齐次变换矩阵0T6为:
0T6=0T11T22T33T44T55T6
(1)
现有的误差模型一般在式(1)基础上取微分,以获得0T6中各个元素与DH参数之间的误差传递关系。由于每个齐次变换矩阵相乘存在正余弦函数耦合,因此微分的解析表达式很复杂。笔者在非线性方程线性化的基础上,将微分运动及其运动旋量与DH参数法相结合,提出一种可以快速求解得到误差传递关系的新算法。当DH参数存在偏差时,连杆i坐标系相对于连杆i-1坐标系,齐次变换矩阵的偏差为Δi-1Ti;协作机器人末端坐标系相对于基座坐标系,齐次变换矩阵的偏差为Δ0T6。在忽略矩阵偏差二阶小量的前提下,可以得到:
=0T6+Δ0T1·1T22T33T44T55T6+0T1
·Δ1T2·2T33T44T55T6+…
+0T11T22T33T44T5·Δ5T6
(2)
应用齐次变换矩阵T的正交性,可以快速求解出逆矩阵T-1[6]。齐次变换矩阵的偏差可以认为由齐次变换矩阵的微分运动所产生,根据文献[7]阐述的坐标系微分运动与坐标系角速度矢量ω、速度矢量v之间的关系,得到:
(3)
(4)
式中:ΔT为齐次变换矩阵T的偏差;δT为齐次变换矩阵T的微分变换矩阵;ω1、ω2、ω3依次为角速度矢量ω沿坐标系X0轴、Y0轴、Z0轴的三个分量;v1、v2、v3依次为线速度矢量v沿坐标系X0轴、Y0轴、Z0轴的三个分量;γ为由角速度矢量和线速度矢量组成的运动旋量。
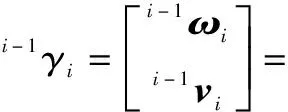
(5)
式中:i-1γi为齐次变换矩阵i-1Ti微分运动的运动旋量;i-1ωi和i-1vi分别为齐次变换矩阵i-1Ti微分运动的角速度矢量和速度矢量;Δαi为相邻关节轴夹角偏差;Δai为连杆长度偏差;Δdi为连杆偏距偏差;Δθi为关节转角偏差;ΔXi为第i个连杆的DH参数矢量偏差;i-1Li为第i个连杆DH参数偏差与运动旋量i-1γi之间的关系传递矩阵。
对式(2)等号两侧消去0T6,即等号两侧同时乘以0T6-1,可以得到:
(6)
式中:0γ6为在基座坐标系下协作机器人末端坐标系微分运动的运动旋量;Ad(j-1Tj)为李代数群中对齐次变换矩阵j-1Tj的伴随变换[8];j为连杆编号中间变量,j=1,2…,i。
结合式(5)和式(6),由运动旋量中提取协作机器人末端位置误差矢量[9],得到:
ΔX=J·ΔX
(7)
(8)
式中:p1、p2、p3依次为协作机器人末端位置矢量p在X0轴、Y0轴、Z0轴三个方向上的分量;Δp为协作机器人末端位置误差矢量;p∧为由协作机器人末端位置矢量p生成的反对称矩阵;I3为三阶单位对角矩阵;ΔX为协作机器人DH参数矢量偏差;J为雅可比矩阵。
笔者通过将运动旋量与DH参数相结合,推导出了协作机器人DH参数标定所需的雅可比矩阵J的快速计算方式。
3 DH参数标定算法仿真
采用最小二乘法对协作机器人的DH参数进行标定[10]:
(9)
在求解雅可比矩阵J的过程中,采用了线性化方法对非线性模型进行简化,需要使用最小二乘迭代法修正DH参数,使修正后的DH参数接近实际DH参数。
通过仿真验证DH参数标定迭代算法的有效性。首先在协作机器人模型DH参数附近选取一组数据,作为协作机器人的实际DH参数,见表2。然后通过随机数生成36组关节角度,分别计算出协作机器人末端的理论位置和实际位置,获得位置误差矢量Δp。最后根据关节角度、协作机器人DH参数和协作机器人末端位置,由式(7)计算雅可比矩阵J。
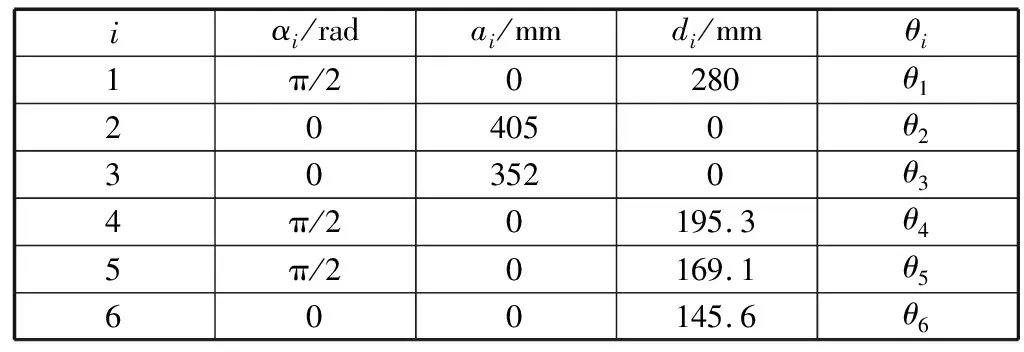
表2 协作机器人实际DH参数
通过最小二乘法迭代十次,协作机器人修正后的DH参数见表3。对比表2和表3数据,修正后的DH参数非常接近仿真中选取的协作机器人实际DH参数。绘制在每次迭代过程中Δp的二范数变化情况,如图2所示。由图2可以看出,Δp的二范数快速收敛至0。首次迭代后Δp的二范数为0.06 m,第十次迭代后为1×10-7m。在标定后,协作机器人末端位置精度提高99.9%。这一仿真结果验证了笔者提出的基于微分变换的DH参数标定方法的有效性。
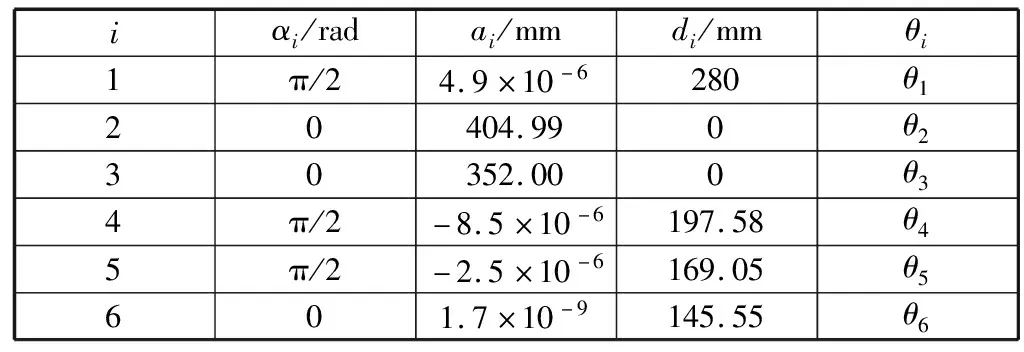
表3 修正后协作机器人DH参数
4 标定板设计
协作机器人具有良好的人机交互特性,在协作机器人使用过程中,可以手动拖动协作机器人的末端至所需要的位置。应用协作机器人的这一特性,笔者设计了用于协作机器人DH参数标定的标定板,如图3所示。在标定板上,有一些直径一致的圆孔,这些圆孔可以与协作机器人末端法兰紧密贴合。在标定过程中,操作者可以将协作机器人末端拖动至标定板的不同孔位中。
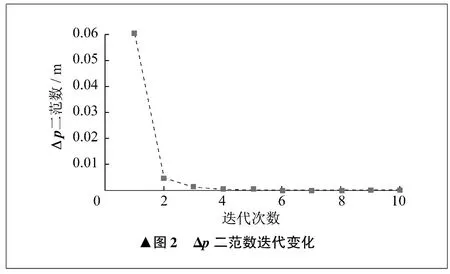
▲图2 Δp二范数迭代变化
由于协作机器人底座与标定板通过两个固定销固定,保证了协作机器人底座与标定板之间的相对位置关系为唯一确定,标定板上每个圆孔在机器人基座标系中的位置均可以通过标定板的几何尺寸获得。在标定过程中,操作者不需要使用激光跟踪仪或高精度相机对协作机器人末端进行位置测量。标定板的使用极大简化了协作机器人DH参数标定的操作过程。

▲图3 协作机器人及标定板
5 试验验证
在标定过程中,拖动协作机器人末端法兰至标定板孔位中,读取协作机器人各关节角度数据和末端位置数据,计算出位置误差矢量Δp和雅可比矩阵J,便可对DH参数进行标定。为保证协作机器人的逆运动学求解有解析解,在试验迭代修正的过程中,增加了保持DH参数中αi不变的约束条件。这一条件保证了在迭代过程中,协作机器人运动学模型相邻关节保持绝对平行或绝对垂直的状态。拖动协作机器人末端法兰至标定板上12个圆孔,分别记录各关节转角,进行十次迭代后,得到试验DH参数,见表4。
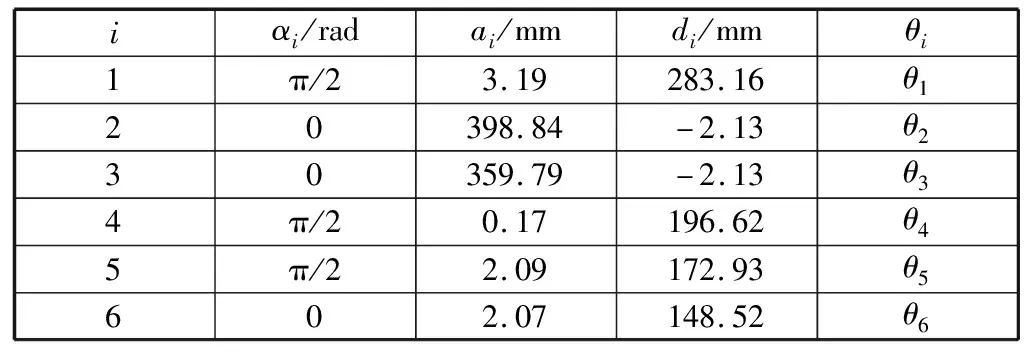
表4 协作机器人试验DH参数
试验过程中Δp的二范数随迭代次数的变化情况如图4所示。由图4可以看出,第三次迭代后,Δp的二范数趋于稳定。第一次迭代时,Δp的二范数为0.045 m。第十次迭代后,Δp的二范数为0.007 3 m,末端位置精度提高84%。试验验证了笔者所提标定方法的有效性。
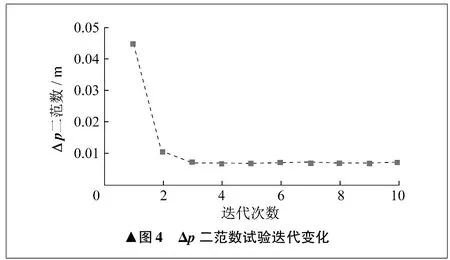
▲图4 Δp二范数试验迭代变化
为进一步验证修正DH参数的可信性,在标定板中另外选取三个未纳入标定数据采样的圆孔。将协作机器人末端拖至这三个圆孔中,通过修正DH参数计算协作机器人的末端位置偏差,并与初始末端位置进行比较,结果见表5。
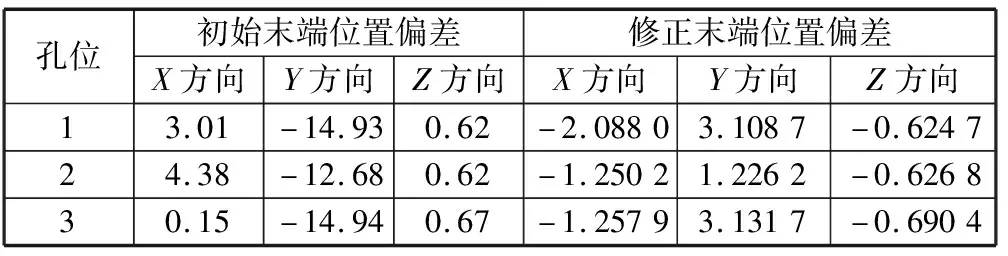
表5 协作机器人位置偏差比较 mm
由表5可以看出,使用修正DH参数后,协作机器人在标定板其它位置处的末端位置计算值与实际值偏差减小,偏差的二范数减小76%,进一步验证了标定方法的有效性。当然,在精度上仍然还有较大的提高空间,造成这种现象的原因包括标定数据量太少、扭转角变化约束限制等[11]。
6 结束语
笔者提出了一种基于微分变换的协作机器人误差模型计算方法,避免了复杂的求导计算过程,提高了误差模型的计算效率。在仿真中,通过有限次最小二乘法迭代后对DH参数进行修正,协作机器人末端位置精度提高99.9%。笔者针对协作机器人设计了一种标定板,用于对协作机器人DH参数进行标定。通过试验中十次迭代计算,协作机器人末端位置精度提高了84%。这一基于标定板的协作机器人DH参数标定方法对协作机器人DH参数的实际应用具有参考价值。

