一种新的航空发动机总体性能稳态模型修正方法
樊 巍,施 洋,曹铭栋,刘 勤,陈宣亮
(1.中国航发四川燃气涡轮研究院,成都 610500;2.上海交通大学成都先进推进技术研究中心,成都 610000)
1 引言
航空发动机总体性能稳态计算模型是评估发动机性能的重要手段。对于基于部件法的总体性能计算模型来说,部件特性的准确性对于稳态模型计算的准确性往往具有决定性作用。在发动机前期设计中,通常采用部件通用特性或部件试验特性对发动机总体性能进行计算。但在发动机实际设计和试验过程中,由于装配加工、性能衰减、试验中控制规律调整等原因,使得发动机实际工作中的部件特性与设计阶段给定的部件特性发生偏差,无法对实际发动机状态进行准确预测和分析[1]。因此,有必要开展基于部件法的总体性能稳态模型修正方法研究,以提高模型的计算精度。
目前,针对发动机总体性能稳态计算模型的修正方法开展了大量的研究工作,且多数是通过修正部件特性来提高总体性能稳态计算模型的精度,主要采用的方法有遗传算法[2-3]、模型辨识[4]、部件特性自适应[5]、逆算法[6]等。但以上方法往往需要利用计算机开展大量的运算,计算效率较低,无法达到快速修正模型的目的。本文以某型双轴涡扇发动机地面节流性能试验数据为例,在基于部件法的总体性能稳态计算模型和试验分析模型基础上,通过构建部件特性修正系数和试验测量参数之间的非线性方程组,建立了一种采用牛顿迭代法求解部件特性修正系数的新方法,可实现发动机总体性能稳态模型的快速修正。
2 总体性能稳态模型修正方法
2.1 总体性能稳态计算模型
根据文献[7]建立了基于部件法的发动机总体性能稳态计算模型,可实现包括风扇、压气机、燃烧室、涡轮、混合器、尾喷管等部件的总体性能稳态计算。在控制规律和进气条件一定的条件下,给定风扇、压气机、燃烧室、涡轮等部件特性,通过进行非设计点性能计算,可获得发动机截面气动热力参数和总体性能参数。根据文献[8-9]建立了发动机试验性能分析模型,通过测取的发动机截面参数和燃油流量、推力、转速等参数,根据流量平衡、功率平衡等约束方程,采用变比热计算方法,即可获取各部件性能及各截面参数。
2.2 总体性能稳态模型修正方法
部件特性修正系数k定义为:

式中:xmodel代表部件特性修正后模型实际使用的特性参数值;xmap代表修正前部件特性图上得到的参数值,为常数。
假定发动机试验过程共获得m个测量参数,定义为,如推力、主燃油流量、进口空气流量、压气机出口压力、温度等;共有待修正的n个部件特性参数,定义为,如风扇进口换算流量、压气机压比、涡轮效率等。则测量参数与部件特性参数具有如下关系:


式(2)和式(3)中:f和g函数代表了发动机热力计算过程[9],本文不再赘述。
对于式(3)的非线性方程组,采用牛顿迭代法[10]进行求解。根据发动机实际测量参数情况,定义偏差函数为:

式中:Xmodel代表修正后模型计算获取的参数,Xtest代表试验测量的参数值。当偏差函数满足设定的精度要求时,则认为模型修正结果满足要求。
2.3 对模型修正过程中一些问题的讨论
2.3.1 参数选择
采用牛顿迭代法进行求解,只有当式(2)中的m=n时方程才有唯一解。在发动机试验过程中,通常存在测量参数与部件特性修正系数数量不相等的情况,为保证方程求解,需要对方程的自变量和因变量数量进行增减,且一般建议采取以下两种方式进行处理:
(1) 当m<n时,根据发动机试验分析模型获得的分析结果,或参照发动机总体方案设计参数,增加截面温度或压力参数;
(2) 当m>n时,根据经验或参数敏感性分析结果,对试验结果判定影响较小的测量参数进行删减。
另外,参照Kurzke[11]提出的方法,对于风扇和压气机部件,当导叶角度和转速一定时,部件特性的修正主要依赖流量、压比、效率和β值(特性辅助线)4个参数,为保证解的有效性,只能选择流量、压比、效率中的两个参数进行修正。通过计算分析,压比对于发动机温度或推力等参数的影响并不敏感,有可能需要进行大幅度的修正才能达到目标值,获取的修正压比很有可能已超出实际的设计结果,所以一般选择流量和效率进行修正。
2.3.2 初值给定
初值选择的合理性对于非线性方程组的求解至关重要,初值选择不合适很有可能遇到方程无法收敛的问题。本文中,模型中给定的设计点参数,即为求解2.2节中非线性方程组的计算初值。对于特定状态的发动机(给定进气温度、进气压力和控制规律),可以采用两种方法给定计算初值:一是将发动机模型修正前的设计点作为初值,对于不同的工作状态,其设计点参数不发生变化;二是将通过发动机试验分析模型计算获取的部件参数及循环参数作为设计点带入发动机总体性能计算模型中,对于不同的工作状态,其设计点根据发动机试验测量参数的变化发生改变。计算发现,由于发动机实际工作状态与模型修正前的设计点工况差异较大,采用第一种初值给定方法,极有可能使得初值大幅度偏离方程真实解,从而导致不收敛的情况发生;对于第二种初值给定方法,因为是基于测量参数获取的设计点参数,与方程真实解偏离程度不大,可有效避免不收敛的情况发生,并大幅度提高收敛速度。据此,建议采用第二种初值给定方法开展模型修正,下文也采用这种方法开展算例验证。
2.3.3 收敛误差设置准则
对于发动机试验测量参数,总会存在一定的测量误差,尤其是截面温度和压力测量参数。除了测量探针固有的测量误差外,由于截面测量参数一般是将测量数据通过数学平均获得,没有考虑发动机内部复杂的流动情况,使得平均获得的截面参数很可能受流场影响而出现较大误差。另外,对于构型较为复杂的发动机,发动机总体性能计算模型的准确性除了受部件特性约束外,往往还要受到空气系统等方面的影响。考虑到以上因素,本文针对式(4)中不同的测量参数偏差函数设置不同的精度要求。根据工程应用实际,沿气流流动方向靠后的截面测量参数误差设置为1.5%,沿气流流动方向靠前的截面测量参数以及推力、燃油流量等其他参数误差设置为1.0%。
3 算例及验证
以某型双轴混排涡扇发动机为例,利用其某次地面台架试验稳态性能,对本文提出的方法进行验证。发动机结构示意图及截面定义见图1。

图1 发动机结构示意图及截面定义Fig.1 Engine layout and section definition
在给定发动机进口条件和控制规律的情况下,需要修正的部件特性参数共计12个,分别为风扇进口换算流量Wa,F,c、风扇效率ηF、压气机进口换算流量Wa,C,c、压气机效率ηC、燃烧室总压恢复系数σcomb、燃烧室效率ηcomb、高压涡轮效率ηHT、高压涡轮换算流量Wg,HT,c、低压涡轮效率ηLT、低压涡轮换算流量Wg,LT,c、外涵总压恢复系数σduct、喷管速度系数cv。以上参数对应的修正系数依次为。试验中测取的参数共计12个,分别为发动机净推力F、燃油流量Wf、发动机进口空气流量Wa,2、风扇出口总压p25、风扇出口总温T25、压气机出口总温T3、压气机出口总压p3、高压涡轮出口总压p43、低压涡轮出口总温T5、低压涡轮出口总压p5、外涵道出口总温T16、外涵道出口总压p16。部件特性修正系数与测量参数数量一致,由2.2节方法建立非线性方程组,对应式(3)中的和分别为:
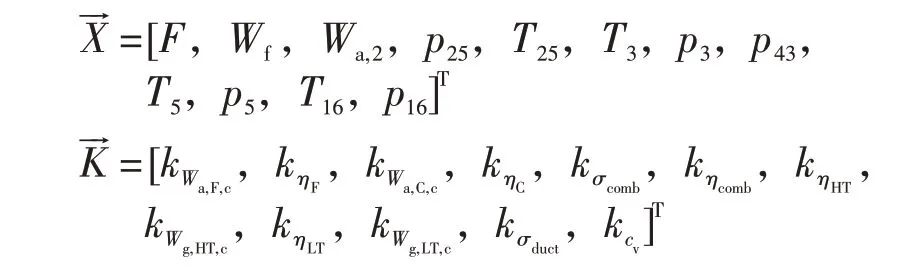
根据2.3.3节收敛误差设置准则,将p43、T5、p5的偏差函数精度设置为1.5%,其余测量参数的偏差函数精度设置为1.0%。
表1对比了发动机工作在高压相对物理转速-nc=97.6%时,模型修正前后的计算结果与试验测量结果的相对误差。可以看出,采用本文方法,发动机模型计算精度明显提高。
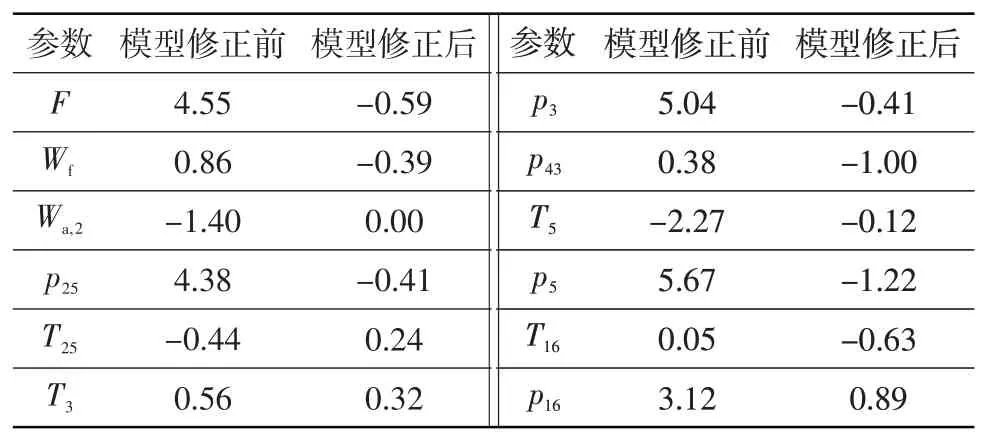
表1 模型修正前后的计算结果与试验测量结果的相对误差 %Table 1 Relative error of calculation results and test data before and after modification
对该发动机地面不同转速工作状态的稳态模型也进行了修正,修正后的计算结果与试验测量结果的相对误差如表2所示。可以看出,模型修正后计算的发动机节流特性与试验实际的特性结果相比,各状态的误差均较小(最大不超过1.5%),计算精度满足工程实际需求。
4 结论
在基于部件法的总体性能稳态计算模型和试验性能分析模型基础上,从发动机实际工作情况出发,构建了部件特性修正系数和试验测量参数之间的非线性方程组,并采用牛顿迭代法对其进行求解,获取了部件特性修正系数,实现了总体性能稳态模型的快速修正。以双轴涡扇发动机为例对本文提出方法进行了验证,与实际试验结果相比计算误差小于1.5%,表明本文提出方法可有效提高发动机总体性能稳态模型计算精度,满足工程应用需求。

表2 模型修正后的计算结果与试验测量结果的相对误差 %Table 2 Relative error of calculation results and test data after modification

