转静轴向间距对压气机静子叶片气流激励的影响

汪松柏，张少平，李春松，刘小凤

(中国航发四川燃气涡轮研究院，成都 610500)

1 引言

航空发动机结构故障中，压气机叶片故障占有相当高的比例。叶片故障绝大部分为疲劳所致，主要原因是叶片振动应力较大和动强度设计不足，而影响叶片动应力大小的主要因素是叶片振动特性和非定常气流激振力。因此，保证叶片具有良好的振动特性和减小气流激励，是降低叶片动应力的主要途径。

现代高性能航空发动机为减轻质量，采用较小的轴向间距设计，加剧了叶排间的转静干涉，导致叶片工作环境恶劣、动应力增加，从而引起叶片高周疲劳失效[1-4]。转静轴向间距作为影响压气机级间非定常干涉的关键参数，一直是国内外学者关注的重点。Valkov[5]和Sirakov[6]研究发现，对于亚声速压气机，轴向间隙的减小对总压比和效率均有一定程度的提升，其原因是尾迹在下游转子通道中恢复导致掺混损失减小。Gorrell[7]发现，轴向间隙减小，跨声速压气机的堵塞流量、效率和总压比都会相应减小，主要是下游转子激波与上游静子尾迹干涉导致损失增加。史亚锋等[8]也得到类似结论。Clark等[9]研究了转子激波与上游导叶尾迹相互干扰引起的非定常现象，特别是激波对静叶尾缘旋涡以及吸力面边界层发展的影响。刘东健等[10]数值研究了转静子叶片排轴向间距对压气机内部流动堵塞及气动性能的影响。上述研究主要关注了转静轴向间距对压气机气动性能的影响，而在压气机的实际使用和试验中，静子叶片由于气流激振导致高周疲劳失效也经常发生[11-14]。为此，有必要研究转静轴向间距对压气机静子叶片非定常气流激励的影响。

关于转静干涉下压气机静子叶片的气流激励问题，赵奔等[15]研究了组合多级压气机中上下游动叶尾迹和势流对中间导流叶栅气流非定常流动的同频和异频叠加干涉特性；赵军等[16]研究表明，在压气机静子结构设计中，需慎重考虑下游跨声速转子产生的非定常气动力对上游静叶高周疲劳寿命的影响。但上述研究只考虑了固定轴向间距下静叶的气流激励，未考虑轴向间距变化的影响。Darbe等[17]研究了单级压气机进口导叶与下游转子轴向间距变化对导叶表面非定常压力载荷的影响，但未考虑多级环境；胡骏等[18]试验研究了单级低速轴流压气机中上游转子与下游静子轴向间距变化对静子叶片气动力的影响，由于流动为亚声速，轴向间距变化对静叶非定常气流激励的影响较小。

对于多级跨声速压气机静子叶片的非定常气流激励，下游转子激波和上游转子尾迹的双重作用会对中间静子叶片产生复杂的非定常干扰。某跨声速压气机试验后第二级静子叶片出现高周疲劳裂纹问题，动应力试验显示下游转子激起较高的振动应力，如何给定合理的转静轴向间距已成为压气机静叶高周疲劳设计的一个难点。本文采用非定常数值方法模拟某3.5级跨声速压气机的三维非定常流场，通过对静子叶片表面非定常压力波动进行频域分析，建立了静子叶片非定常气流激励与上下游叶片通过频率的关系；重点分析了不同转静轴向间距对压气机第二级静子叶片表面非定常气流激励的影响规律。

2 研究对象及数值计算方法

2.1 研究对象

以某3.5级跨声速压气机为研究对象，非定常计算域包括5个导向器通道、4个一级转子通道、6个一级静子通道、5个二级转子通道、10个二级静子通道、6个三级转子通道、10个三级静子通道。网格离散采用IGG/AutoGrid5模块生成，计算域网格总节点数约为1 200万。采用H-O型结构化网格，进、出口延伸段均为H型网格，叶片通道为O型网格。叶顶间隙采用蝶形拓扑结构，间隙内网格层数为9，近壁面第一层网格为10-6m，无量纲参数Y+≈1。计算模型网格如图1所示。

图1 数值计算网格Fig.1 Computational meshes

2.2 时间步长及边界条件

采用商用软件ANSYS_CFX模拟压气机内部三维非定常流场，非定常流场计算以收敛较好的定常计算结果作为初场迭代。选取第三级转子单个通道旋转所用时间为一个周期(T)，每个周期包含20个物理时间步长，时间步长为1.519 76×10-6s。计算边界条件：进口轴向进气，总温为288.15 K，总压为101 325 Pa；出口给定平均静压，湍流度为5%；固体边界采用绝热壁面、无滑移边界条件。湍流模型选取SST模型。定常计算时转静交界面选周向平均的混合平面(Stage)，非定常计算时交界面选取动静叶滑移边界(Transient rotor-stator)。

2.3 转静轴向间距设置

动应力试验发现，第二级静子叶片较大振动应力是由下游转子激起的，故本文主要考查该第二级静子叶片与下游转子的轴向间距变化对其非定常气流激励的影响规律。对于第二级静子叶片与下游转子轴向间距的变化，将原始模型第二级静子和第三级转子交界面后的通道整体平移，在网格划分时使其网格数量与原网格保持一致。对转静轴向间距变化作归一化处理，取无量纲参数Δ分别为0.3、0.4、0.5、0.6、0.7等5种情况作为算例进行分析。参数Δ定义如下：

式中：L为第二级静子叶片尾缘与第三级转子叶片前缘叶根子午面轴向长度，B为第二级静子根部子午面轴向长度。压气机子午面外形及参数定义如图2所示。

图2 压气机模型及参数示意图Fig.2 Sketch map of compressor and its parameters

3 计算结果分析

3.1 轴向间距对气动性能的影响

图3是采用定常数值计算方法得到的5种不同转静轴向间距下压气机的气动特性图。从图中可看出，转静轴向间距变化对总压比和裕度影响较小。随着转静轴向间距增大，压气机的绝热效率先增大后减小，存在一个绝热效率最大值。5种转静轴向间距中，Δ=0.5时的绝热效率最大。由于压气机一般工作在高效率点附近，因此下文的非定常计算分析都是以最大效率工况进行。

图4为第三级转子和第二级静子叶片80%叶高截面的静压分布。由图可知，第三级转子吸力面30%弦长位置附近存在激波。从第二级静子叶片一个周期的静压波动可看出，静叶表面静压波动剧烈，前缘主要受上游第二级转子尾迹的影响，中间至尾缘段受下游第三级转子激波的影响，且激波产生的静压波动明显较尾迹强烈。激波与叶片附面层的相互干扰，是跨声速压气机流动损失的一个重要来源。第三级转子前缘激波与上游静子叶片附面层的干扰随轴向间距的增大而减小，导致损失相应减小，这是Δ由0.3增至0.5时压气机绝热效率增大的主要原因。随着转静轴向间距进一步增大，静子尾迹强度逐渐减弱、宽度增大，尾迹导致的压力波动幅度沿流向随着转静轴向间距增大逐渐减弱。从图5第三级转子进口时均轴向速度周向分布规律可知，随着轴向间距增大，第二级静子叶片尾迹波动幅度减弱、宽度增加。尾迹轴向速度波动幅度减小导致尾迹恢复数减小，从而造成压气机性能有所降低，这与文献[19-20]的研究结论相一致。可初步认为，可能存在一个最佳的转静轴向间距，既保证压气机绝热效率处于较高水平，同时又使得压气机静子叶片非定常气流激励相对较小。

图4 Δ=0.3时第三级转子和第二级静子叶片80%叶高截面静压分布Fig.4 Static pressure distribution of R3 and S2 for Δ=0.3 at 80%span

图5 第三级转子20%和80%叶高进口轴向速度的周向分布对比Fig.5 The mean inlet axial velocity of downstream rotor R3 at 80%and 20%span

3.2 静子叶片表面压力载荷频谱分析

为探究转静轴向间距对压气机静子叶片表面压力载荷的影响，非定常计算过程中，对不同转静轴向间距下第二级静子叶片80%和20%叶高截面前尾缘表面静压进行监测，监测点位置如图6所示。

图6 第二级静子叶片表面静压监测点Fig.6 Monitoring point positions of static pressure at S2 blade surface

图7给出了Δ=0.3时静子叶片80%叶高前缘监测点表面静压随时间变化的频谱结果。从图中可看出，静子叶片表面压力载荷受上下游叶排转静干涉影响波动剧烈，下游转子产生的气流激励频率幅值约为上游转子的2倍。非定常数值计算收敛时，静子叶片表面压力随时间周期性波动。

图7 Δ=0.3时前缘静压监测点的时域和频域图Fig.7 Time and frequency analysis of static pressure at leading edge for Δ=0.3

对按时间变化的压气机第二级静子叶片表面4个监测点静压进行快速傅立叶变换和频谱分析，其结果如图8～图11所示。

图8 不同轴向间隙下80%叶高前缘点静压频谱Fig.8 Frequency spectrum analysis of static pressure at 80%span leading edge for different axial spacings

图9 不同轴向间隙下80%叶高尾缘点静压频谱Fig.9 Frequency spectrum analysis of static pressure at 80%span trailing edge for different axial spacings

图10 不同轴向间隙下20%叶高前缘点静压频谱Fig.10 Frequency spectrum analysis of static pressure at 20%span leading edge for different axial spacings

图11 不同轴向间隙下20%叶高尾缘点静压频谱Fig.11 Frequency spectrum analysis of static pressure at 20%span trailing edge for different axial spacings

从图8、图9中可看出，对于80%叶高截面，静子叶片前、尾缘表面非定常气流激励的主导频率均为R3-1BPF(R3激起的1倍频，叶片通过频率BPF=(转速/60)×叶片数)，即静子叶片表面非定常压力波动主要受下游转子的影响，且这种影响可从静子叶片尾缘传播至前缘。对于前缘监测点，还存在R2-1BPF(R2激起的1倍频)，其幅值较R3-1BPF的小，即静子叶片前缘非定常压力波动同时受到上游转子尾迹和下游转子的影响，气流激励的主导频率为下游转子的通过频率。从尾缘监测点频谱看，未见上游第二级转子的激励频率，说明上游转子对静子尾缘的气流激励作用较弱。同时，尾缘监测点频谱中可见R3-2BPF成分，这是下游转子前缘激波与上游静子尾迹干涉形成的高阶频率——文献[16]中也观察到类似的高阶倍频成分。从不同转静轴向间距静子叶片表面监测点气流激励主导频率(R3-1BPF)幅值看，随着转静轴向间距增大，下游转子对上游静子叶片的气流激励频率幅值明显下降。相较于Δ=0.3，Δ=0.5时前缘点气流激励幅值下降了19.7%，尾缘点气流激励幅值下降了31.1%；Δ=0.7时前缘点气流激励幅值下降了26.8%，尾缘点气流激励幅值下降了44.6%。从气流激励幅值与轴向间距的变化规律看，随着转静轴向间距增大，气流激励频率幅值下降斜率逐渐减小，说明一定轴向间距范围内，气流激励强度与转静轴向间距的敏感性随轴向间距的增大而减弱。压气机设计过程中，满足气动设计的同时，适当增加转静轴向间距，在减小叶片气流激励方面可获得较大收益。

从图10、图11中可看出，对于20%叶高截面，第二级静子叶片前缘表面非定常压力波动的主导频率为R3-1BPF和R2-1BPF。随着转静轴向间距增大，下游第三级转子对第二级静子叶片前缘表面非定常压力的影响逐渐减弱，上游第二级转子对其的影响基本不变。当Δ增大到0.5后，第二级静子叶片前缘表面非定常压力波动的主导频率为R2-1BPF，此时上游转子对其气流激励作用最强。同时，静子前缘表面非定常压力波动频谱中出现了R2-2BPF成分——文献[18]一级低速轴流压气机试验中下游静子叶片前缘也出现了类似的高阶频率成分，这是由于尾迹和势流造成气动参数不均匀形成。第二级静子叶片尾缘表面非定常压力波动的主导频率为R3-1BPF，其幅值随轴向间距的增大而减小。由于下游转子低叶高区无激波，第二级静子叶片尾缘监测点静压波动频谱中不存在高阶倍频现象。从不同转静轴向间距主导频率(R3-1BPF)幅值看，相较于Δ=0.3，Δ=0.5时前缘点气流激励幅值下降了33.1%，尾缘点气流激励幅值下降了48.1%；Δ=0.7时前缘点气流激励幅值下降了53.5%，尾缘点气流激励幅值下降了66.1%。从静子叶片4个监测点的气流激励频谱规律看，当下游转子工作在跨声速工况时，会对上游静子叶片产生较强的非定常气流激励，其激励范围可传播至上游静子前缘，需要特别慎重的抗高周疲劳设计。

3.3 静子叶片表面压力波动对比

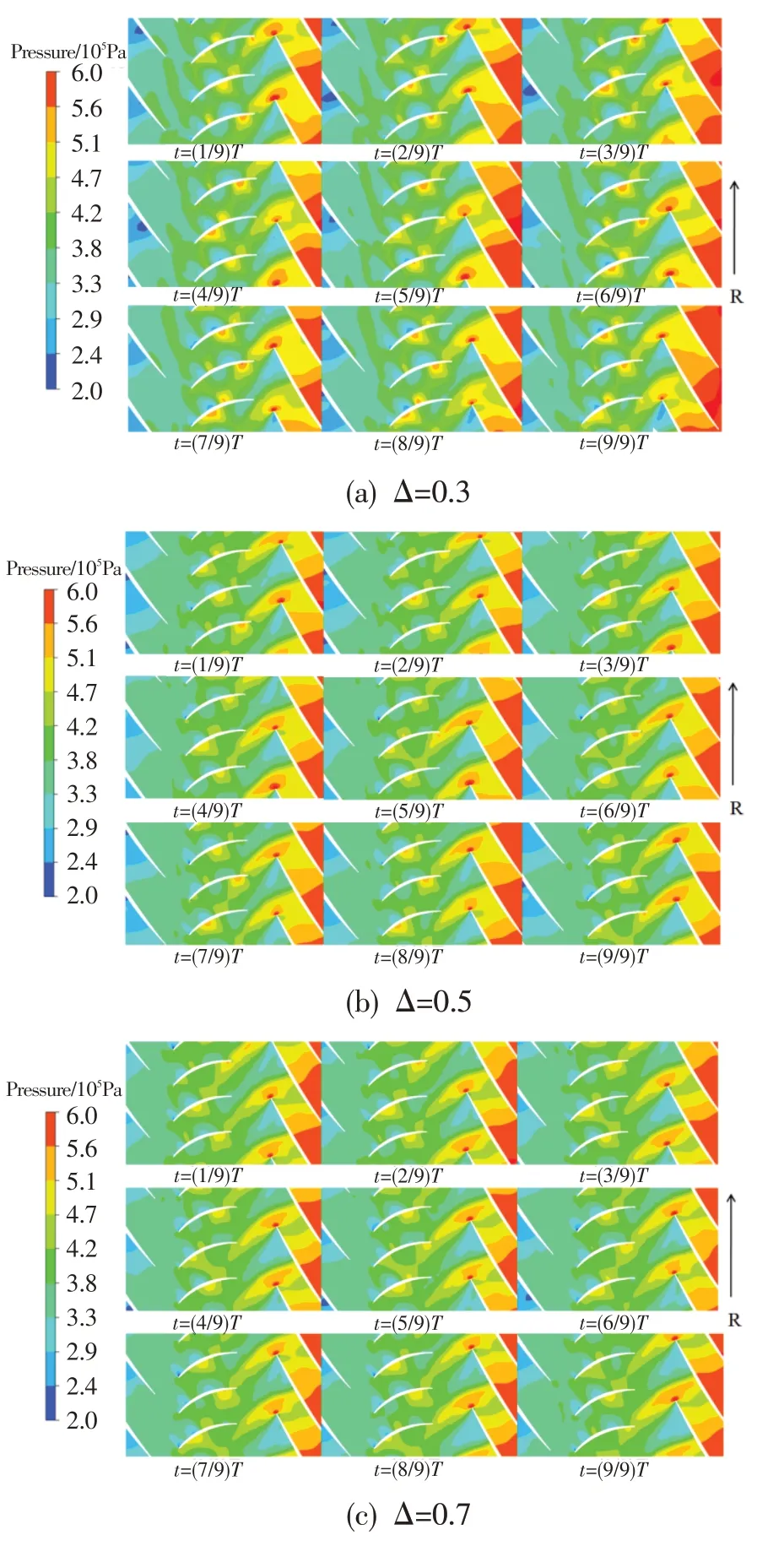
图12 80%叶高截面静压云图Fig.12 Contour of static pressure at 80%span section

图12为Δ=0.3、0.5、0.7三个典型方案第二级静子叶片在上下游转子作用下80%叶高截面一个周期内的静压分布情况。可看出，叶片尾缘明显受到下游第三级转子前缘激波的影响，导致表面静压波动剧烈。下游转子前缘激波从上游静子尾缘吸力面向前缘传播，随第三级转子转动被下一个静子尾缘切割后，下部分激波在静叶压力面侧形成压力波扰动并向上游前缘方向传播，传播方向与主流方向相反，压力波强度逐渐减弱。随转子转动，整个压力面侧都受到下部分激波的扰动；吸力面侧受激波直接作用，静压波动较大。同时，静子叶片前缘吸力面侧存在明显的低压区，这是由于尾迹/势流产生的扰动，对吸力面的影响区域可达50%弦长位置。上游转子尾迹/势流和下游转子前缘激波的双重作用导致静子叶片吸力面静压变化较大，其波动较压力面的剧烈。随着转静轴向间距增大，Δ=0.5和Δ=0.7时下游转子前缘激波对上游静子叶片表面静压的影响减小，静子叶片表面压力波动明显减弱。

图13 80%叶高截面静压的时空图对比Fig.13 Comparison of pulsatile stator blade surface static pressure distribution at 80%span section

图13为Δ=0.3和Δ=0.7时第二级静子叶片80%叶高截面表面非定常压力波动的时空图。图中，LE、TE分别表示叶片的前缘和尾缘；PS、SS分别表示叶片压力面和吸力面；Δp/p0表示瞬时静压波动值，其中Δp为瞬时静压值与一个周期内时均值之差，目的是消除时均值以反映流场中的非定常压力波动。从图13(a)中可以看出，静子叶片在上下游叶排转静干涉下表面非定常压力波动剧烈，吸力面波动幅值约为压力面的2倍。吸力面侧受下游转子前缘激波的直接作用，中部弦长位置波动最强烈。同时，吸力面侧明显可见上游转子尾迹/势流和下游转子前缘激波交替作用形成的低、高压区，二者的共同作用导致吸力面非定常压力载荷波动强烈。压力面侧压力载荷波动主要是切割后的下部分激波向上游传播所致，其压力载荷波动幅值较激波直接作用弱。当轴向间距增大到Δ=0.7时，静子叶片表面非定常压力波动情况较Δ=0.3的明显减弱，且吸力面波动幅值与压力面的基本相当，此时静子叶片气流激励强度明显减弱。

综合上述不同转静轴向间距方案下跨声速压气机气动性能和第二级静子叶片表面压力非定常气流激励分析，可以认为存在一个最佳转静轴向间距，既满足压气机绝热效率处于较高水平，又使得压气机静子叶片非定常气流激励相对较小。针对本文研究的5种转静轴向间距模型，认为该跨声速压气机第二级静子与第三级转子叶排间轴向间距Δ=0.5时最佳。压气机叶片设计过程中，叶排间转静轴向间距的选择须综合考虑气动、结构及振动等各方面的影响。

4 结论

通过数值方法模拟了3.5级跨声速压气机的三维非定常流场，分析了转静轴向间距对压气机静子叶片非定常气流激励的影响。主要结论如下：

(1) 压气机静子叶片非定常气流激励主导激励源为下游转子，下游转子前缘激波产生的压力波动较上游转子尾迹的强烈，是引起静子叶片非定常气动载荷剧烈变化的主要原因；静子叶片结构设计过程中，应重点关注下游转子引起的气流激励因素。

(2) 存在一个最佳转静轴向间距，既满足压气机级效率处于较高水平，同时又使得压气机静子叶片气流激励相对较小；一定范围内，适当增加轴向间距，在降低由下游转子引起的静子叶片气流激励方面可获得较大收益。