基于三维CFD与智能算法的一体化涡轮过渡段气动优化

杨 杰，宋友富，熊清勇，杨伟平

(1.中国航发湖南动力机械研究所，湖南株洲 412002；2.中小型航空发动机叶轮机械湖南省重点实验室，湖南株洲 412002)

1 引言

包括涡扇、涡轴、涡桨在内的多转子燃气涡轮发动机中，由于高、低压涡轮气动和结构上的不同要求，高、低压涡轮之间通常存在较大的转速差和高度差，从而需要一过渡段对高、低压涡轮进行联接[1]。由于涡轮过渡段的气动性能对涡轮部件甚至整个发动机的性能都有重要影响，故国外历来重视对涡轮过渡段的研究。自1967年扩压段的Sovran-Klomp特性图[2]总结开始，国外对过渡段做了大量的研究[3-7]。还制定了一些关于涡轮过渡段的专门研究计划，如欧洲的AITEB-2计划[8]、AIDA计划[9]等。近年来，国内学者对涡轮过渡段的兴趣也开始增长，开展了大量的研究[10-12]。

涡轮过渡段根据结构形式的不同可区分为普通过渡段和一体化过渡段。普通过渡段即扩张流道+支板叶片。一体化过渡段是为了进一步提高涡轮部件的气动性能，同时降低其尺寸和质量，采用过渡段与下游涡轮静子一体化的结构来代替单独的过渡段和下游涡轮静子。从目前能检索到的公开文献看，对于涡轮过渡段的研究主要集中于普通过渡段，且已总结出一些基本的研究规律[13-15]；对于一体化过渡段的研究则相对较少，近年来奥地利Graz大学的Marn和Göttlich[16]、比利时冯卡门流体动力学研究所的Lavagnoli[17]、国内中国航发湖南动力机械研究所的杨杰[18]等进行了一些研究。

相对于普通过渡段，一体化涡轮过渡段的气动性能对于整个涡轮部件气动性能的影响更大，且其设计难度也更大。在一体化过渡段的早期设计阶段，其气动性能通常很难达到性能指标要求，需要在后期进行优化改进。

随着三维CFD技术的持续发展，包括神经网络与遗传算法等在内的智能算法应用的日益广泛，以及计算机工具能力的日益强大，将三维CFD与智能算法相结合的优化技术已逐渐应用于涡轮机械的优化设计领域，并取得不错效果[11]。然而，对于一体化过渡段，由于其几何与流动特征的复杂性，目前针对性的设计优化研究在公开文献中还很少见。

本文以某发动机的一体化涡轮过渡段为研究对象，对基于三维CFD与智能算法的一体化涡轮过渡段的气动性能优化技术开展研究。

2 研究方法

2.1 研究对象

研究对象是发动机的一体化涡轮过渡段，含4个大叶片与8个小叶片，4个大叶片在小叶片中沿圆周均匀分布。其几何模型见图1。

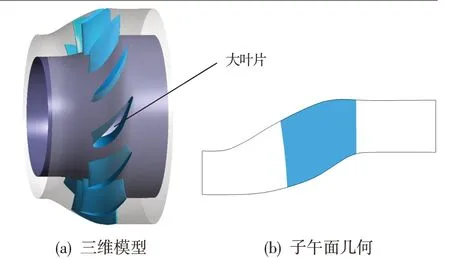
图1 本研究中的一体化过渡段几何Fig.1 The IITD geometry model

2.2 研究工作流程

以Numeca软件的Design 3D模块作为优化平台，以一体化过渡段的性能作为目标函数，以一体化过渡段的几何作为优化变量，通过三维CFD结合神经网络与遗传算法对一体化涡轮过渡段进行迭代寻优。迭代寻优原理为：由三维CFD生成数据样本，由数据样本训练神经网络得到过渡段的优化目标预测函数，通过遗传算法对此预测函数求取极值点，然后对此极值点的过渡段几何进行CFD计算获取性能参数，完成一次迭代过程；将此CFD计算结果加入到神经网络样本数据库中进入下一次迭代，直至达到收敛标准。

研究工作的基本流程为：原始过渡段的流动特征分析→原始过渡段的几何参数化建模→优化方案设定→数据样本生成及迭代寻优→优化结果分析。

2.3 三维CFD数值模型

原始过渡段的流动特征分析、Design 3D平台上神经网络的数据样本生成及过渡段几何迭代寻优过程中的三维流场模拟，通过采用Numeca软件的Fine模块求解定常雷诺平均N-S方程来实现。其中湍流的模拟采用S-A模型。N-S方程的空间离散采用中心格式，伪时间步采用当地时间步。采用两重网格进行加速计算。

一体化过渡段的计算网格采用Numeca软件的AutoGrid平台生成。计算网格中包含1个大叶片和2个小叶片，即计算域为过渡段圆周环的1/4。计算网格的网格量为180万网格节点数。经网格无关性验证，该网格量可保证计算结果不随网格量改变。叶片、内外机匣壁面Y+值控制在5以内。计算网格示意图见图2。

图2 计算网格Fig.2 The computation mesh

计算域进口给定总温、总压、进气方向和来流湍动能、湍耗散，出口给定平均静压。计算域展向两侧、叶片表面给定无滑移壁面边界条件，周向两侧设置为周期性边界。静子区域与转子区域的交接面采用混合面处理方式。

优化前后所有过渡段几何的计算算例的网格拓扑和网格量均相同，湍流模型与边界条件等计算设置均保持一致，这样可以保证计算结果的差异仅由过渡段几何的差异引起。

3 原始过渡段流动特征分析

采用2.3节中的三维CFD数值模型对原始过渡段的流动进行数值模拟。结果表明，原始过渡段的总压损失为5.27%。

图3给出了数值模拟得到的原始过渡段的大、小叶片吸力面与压力面的极限流线图。从图中可看出，原始过渡段在大叶片的吸力面下部存在明显的流动分离区，在大叶片及其左右两侧小叶片的压力面上部也存在明显的流动分离区。正是这些流动分离区域的存在造成原始过渡段的气动损失较大。

图3 极限流线图Fig.3 The extreme streamline

大叶片吸力面下部发生流动分离的原因在于，大叶片吸力面下部的叶型存在较大的扩散度，从而造成大叶片吸力面后段形成较大的逆压梯度，使得流动发生分离。大、小叶片压力面上部发生流动分离的原因在于，过渡段上流道较大的向外扩张度造成了较大的逆压梯度，从而造成上流道与大、小叶片角区发生流动分离。对过渡段的流道与叶型几何进行设计优化以减弱甚至消除分离，是此过渡段性能优化改进的方向。

4 过渡段几何参数化建模

由于原始过渡段流道与叶片几何是由离散的数据点组成，所以在性能优化计算前必须对几何进行参数化，以提取特征参数，减少优化变量数目。

过渡段几何参数化的基本过程是：在对原始过渡段流道与叶片几何分析的基础上，构建过渡段流道与叶片的初始参数化模型，然后对初始参数化模型的流道与叶片参数进行拟合计算，最终获得模型参数值，形成参数化模型。

4.1 流道参数化初始模型

根据对原始过渡段流道几何的分析，上、下流道分别采用16个和15个控制点的Bezier曲线模型进行拟合，控制点的分布见图4。

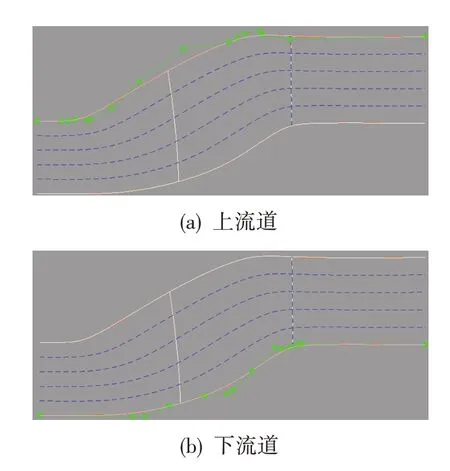
图4 过渡段流道的初始参数化模型Fig.4 The initial parametric model of IITD flow passage

4.2 叶片参数化初始模型

叶片参数化初始模型的构建，包括流面定义、径向积叠规律定义和叶片型线定义三个方面。

4.2.1 流面定义

流面定义确定叶片参数化模型中径向截面的个数及径向截面的形态(平面、圆柱面、锥面、百分比插值面)。由于过渡段流道型线具有较大的爬升角，故考虑采用等百分比插值面作为叶型的径向截面。由于原始过渡段叶片几何给出了6个径向截面的叶型，故可以考虑沿径向0、0.2、0.4、0.6、0.8、1.0展向位置定义6个叶型截面。然而，径向截面过多可能造成优化后叶片沿径向的扭曲过大，采用沿径向0、0.5、1.0展向位置的3截面模型可以避免该问题，故本文研究分别考虑径向6截面(图5)与径向3截面(图6)的叶片参数化模型方案。

图5 径向6截面模型Fig.5 6-radial-section model

图6 径向3截面模型Fig.6 3-radial-section model

4.2.2 径向积叠规律定义

径向积叠规律定义确定叶片的径向积叠方式，包括积叠位置、积叠线形状的定义。积叠位置可选择在前缘、尾缘、重心、最大厚度、通道中心、中型线某位置、弦长某位置。参数化拟合时，结合积叠线形状的定义，以上各位置均可选择，其中选择前缘或尾缘最简洁。积叠线形状包括轴向形状和周向形状。本研究中，积叠位置选在尾缘，积叠线的轴向形状(图7)和周向形状(图8)均采用5节点B样条曲线拟合。

4.2.3 叶片型线定义

叶片型线定义确定叶片型线的构造方式，包括中型线的定义和边型线的定义。中型线可选择简单Bezier曲线(由进口构造角、出口构造角和安装角3个角度定义)或Bezier曲线(由3个或以上控制点定义)，其他还有样条曲线、圆弧线、自定义曲线等，其中简单Bezier曲线最简洁和最直观。本研究中选择简单Bezier曲线(图9)。

图7 积叠线轴向形状Fig.7 The axial shape of the stacking line

图8 积叠线周向形状Fig.8 The circumferential shape of the stacking line

图9 采用简单Bezier曲线的中型线定义Fig.9 The definition of the camber line by simple Bezier curve

边型线可通过厚度控制点和型线控制点两种方式定义。由于型线控制点对于叶型的控制更直观，故本研究中采用型线控制点方式对边型线进行拟合(图10)。吸力面选取3个控制点，压力面选取2个控制点。除进口构造角、出口构造角、安装角、3个吸力面控制点、2个压力面控制点等8个参数外，每个截面还包括弦长、前缘半径、尾缘半径、尾缘楔角等4个参数。

4.3 过渡段几何参数化拟合计算及结果

对过渡段流道和叶片建立参数化初始模型后，以原始流道和叶型几何为拟合目标，采用遗传算法对模型参数进行拟合计算，经多次迭代后得到参数对模型参数进行拟合计算，经多次迭代后得到参数化几何模型结果。

图10 采用型线控制点方式的边型线定义Fig.10 The definition of edge line

径向6截面与3截面模型的拟合结果分别见图11、图12。图中显示，两种参数化建模方案，流道的拟合结果均非常好，与原始流道几乎无差异；而叶片的拟合结果中，径向6截面模型拟合叶型与原始叶型几乎无差异，径向3截面模型拟合结果稍逊，两个小叶片20%展向位置以上的吸力面型线与原始叶片存在较小差异。

图11 径向6截面模型拟合结果Fig.11 The fitting result of 6-radial-section model

图12 径向3截面模型拟合结果Fig.12 The fitting result of 3-radial-section model

5 优化方案

将过渡段几何参数化后，通过选取优化变量及其变化边界进行CFD计算生成数据样本点，然后定义目标函数进行基于神经网络和遗传算法的迭代寻优计算，获得优化结果。

本研究中取过渡段总压恢复系数与流量的加权组合作为目标函数进行单目标优化，其中流量趋向定值，总压恢复系数趋向最大。根据只优化流道、只优化叶片、同时优化流道与叶片三种思路选取优化变量，设定了5种优化方案，见表1。

表1 优化方案Table 1 The optimization scheme

由于原始过渡段中叶片表面的流动存在分离，而叶片进口气流攻角对叶片表面的流动分离有很大影响，故对叶片进行优化时，叶型的安装角和进口构造角为重点优化参数。采用6截面参数化模型时，为减少优化变量数目，未对叶型控制点坐标进行优化。

6 优化结果分析

6.1 优化结果

优化后的过渡段几何见图13～图17，性能计算结果如表2～表6所示。表中，相对进口流量定义为优化后的过渡段进口流量与原始过渡段进口流量之比，原始过渡段的相对进口流量设为1；出口气流角定义为出口气流方向与轴向的夹角；优化前后相对进口流量、进出口静压比、出口马赫数的差异定义为优化值与原始值之差再与原始值之比；优化前后总压损失、出口气流角的差异定义为优化值与原始值之差。

图13 OPT_LD方案流道几何Fig.13 The flow passage geometry for OPT_LD

图14 OPT6S_B方案叶片几何Fig.14 The blade geometry for OPT6S_B

图15 OPT6S_LDB方案叶片与流道几何Fig.15 The blade and flow passage geometry of OPT6S_LDB

图16 OPT3S_B方案叶片几何Fig.16 The blade geometry of OPT3S_B

图17 OPT3S_LDB方案叶片与流道几何Fig.17 The blade and flow passage geometry of OPT3S_LDB

表2 OPT_LD方案气动性能Table 2 The aerodynamic performance of OPT_LD

6.2 结果分析

表中显示，5个优化方案对过渡段的性能均有所提升，但总体而言采用3截面模型优化方案的性能提升效果要优于采用6截面模型优化方案。其中，OPT3S_LDB方案的优化效果最好，总压损失下降1.12%；OPT6S_B方案优化效果最差，总压损失仅下降0.13%。5个优化方案的优化结果均能保证过渡段的进口流量不变，而且进出口静压比、出口马赫数和出口气流角在优化前后变化也很小。

表3 OPT6S_B方案气动性能Table 3 The aerodynamic performance of OPT6S_B

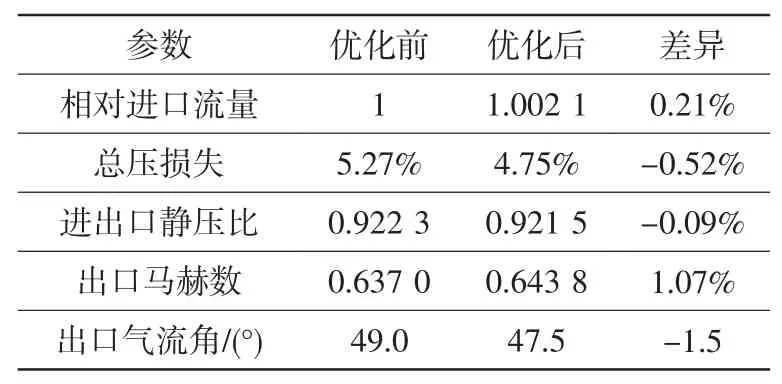
表4 OPT6S_LDB方案气动性能Table 4 The aerodynamic performance of OPT6S_LDB

表5 OPT3S_B方案气动性能Table 5 The aerodynamic performance of OPT3S_B

表6 OPT3S_LDB方案气动性能Table 6 The aerodynamic performance of OPT3S_LDB

图中显示，采用OPT6S_B、OPT6S_LDB方案得到的叶片几何沿展向有较大扭曲，而且其性能优化效果也不是最好，故将其作为最终的优化结果不可取。相比之下，OPT_LD、OPT3S_B、OPT3S_LDB方案的优化结果则可取。

对于叶片几何的优化结果，OPT3S_B与OPT3S_LDB方案的类似，0%展向与100%展向位置的叶型相对于原始叶片几何有较明显变化，而且变化规律一致，均是0%展向位置的叶片几何向吸力面偏转，100%展向位置的叶片几何向压力面偏转。对于流道几何的优化结果，OPT_LD与OPT3S_LDB方案的类似，相对于原始几何均是上流道下压、下流道上抬；上/下流道的曲率相对于原始流道减小、扩散度减小。

图18给出了OPT_LD、OPT3S_B、OPT3S_LDB方案的优化结果与原始过渡段流动特征的对比。可见，此3种优化方案对过渡段的流动状态均有明显改善。其中，OPT_LD和OPT3S_B方案对原始过渡段大叶片吸力面下部和大小叶片压力面上部的流动分离均有一定程度的减弱；OPT3S_LDB方案虽然对大叶片吸力面下部的流动分离有所增强，但对大小叶片压力面上段的流动状态有极大改善，几乎消除了该位置的流动分离。

图18 优化前后叶片表面的极限流线Fig.18 The extreme streamline on blade surfaces before and after optimization

7 结论

对基于三维CFD与智能算法的带大小叶片的一体化过渡段的气动优化技术开展了研究，主要得到如下结论：

(1) 对优化前过渡段流动特征的分析和认识，是识别主要优化变量、取得较好优化效果的必要前提。

(2) 过渡段几何参数化拟合结果的优劣取决于初始模型的构建，初始模型的构建应以对优化前过渡段几何特征的分析为基础，以合适的模型和尽可能少的参数对原始几何进行拟合。

(3) 对于原始过渡段叶片几何为6个径向截面的情形，采用径向3截面模型进行参数化拟合的效果较采用径向6截面模型的效果稍逊，但能有效减少拟合的参数数目，并消除优化结果叶片几何沿径向的扭曲。

(4) 对过渡段叶片与流道同时进行优化的结果，要优于只对叶片或流道进行优化的结果。本文只对流道、只对叶片、同时对流道与叶片进行优化的过渡段，其总压损失降低效果分别达到0.49%、0.56%、1.12%。