工程质量保险与我国工程质量风险契合度分析

马海骋，盛金喜，李慧民

（西安建筑科技大学 土木工程学院，陕西 西安 710055，E-mail：99346242@qq.com）

工程在竣工以后的使用阶段，如果发生质量问题，通常是由施工单位保修或者使用留置的质量保证金进行维修，而质量保证金的留置时间最长不得超过 24个月，超过这个时间后，如果发生质量问题，业主的合法权益难以保障。墙皮脱落，屋顶、楼面、水管、卫生间漏水等现象，给生活带来很多的不便，影响了居民的消费需求。更有甚者，房屋发生偏移倒塌，威胁人们的生命、财产安全，造成严重的社会后果[1]。建筑产品涉及全社会，涉及千家万户，事关广大人民群众的根本利益。发展工程质量保险，可以有效地减少和转移建筑产品的绝大部分质量风险，可以有效减少由于质量问题引起的经济纷争和社会矛盾[2，3]。

工程质量保险制度最早起源于法国，逐步为很多国家所借鉴和引进[4]。其保障的是工程竣工以后的质量风险[5]，保险期最长为10年。例如法国行业协会做过统计，发现在工程完工后 10年内用于质量缺陷的维修费用逐年递减，到第 10年时用于缺陷维修的费用仅为第 1年的 4%，前 10年之和的1.1%[6]；但 10年的保险期与我国的法律规定不一致。根据我国设计规范，对于一般房屋建筑为 50年，特殊建筑为100年。因此工程质量保险就与我国的需求具有一定的差距。政府可以通过行政手段强制要求保险的期限覆盖设计使用年限，但这样势必造成保费的上涨。例如法国业主保险费率原来为建筑工程总造价的1.0%~1.5%（除税外），由于10年前保险公司赔钱，其保险费率调整为建筑工程总造价的3%[7]。因此，工程质量保险保障的期限与我国的实际需求契合多少，是否满足基本需求，就需要进行研究。

鉴于此，本研究对工程不同部位的质量风险、造价、相互影响程度进行分析，确定各因素权重和坐标轴位置关系，通过调研统计我国工程竣工后各年内质量投诉的数量，运用契合度模型，对工程质量保险与我国工程质量风险的契合度进行研究，为我国设计工程质量保险方案提供理论依据。

1 契合度模型建立

对于工程质量保险和实际质量风险需求，可以参考分部工程和保险责任分类，从地基基础、主体结构、防水工程、保温工程、水电安装、装修工程等方面分析。可以对质量风险保障的需求和工程质量保险的供给在这6个方面进行比较。先计算这6个方面的权重，然后得出需求值和供给值对应的坐标值，在对应的轴线上找到需求值和供给值对应的位置。

关于坐标轴的相互位置关系，因为工程质量保险的坐标轴多于3个，因此其有多种排列组合的方式，排序方式不同，将影响最终的计算结果，因此需要对每种方式进行分析，选出最优方案。这里从这6个方面的相互影响程度进行分析，相互影响越大，则坐标轴之间的距离越近。在确定好坐标轴位置关系和需求域和供给域各项的坐标值后，可以画出需求域和供给域（见图1）。其中，阴影部分为供给域和需求域的重叠区域。

图1 契合度分析图

然后，可以计算出供给和需求重叠部分的面积，再与需求域的面积进行比较：

式中，A表示供给和需求的契合度；Sc表示重叠部分面积；Sx表示需求部分面积。

可以看出，A始终≤1，当A越接近1时，表示供给越能满足需求，也就是工程质量保险越能满足实际工程质量风险保障的需求。

式中，F表示供给程度；Sg表示供给部分面积。

可以看出，当F>0时，表示供给存在超过需求的部分，但供给不一定满足了所有的需求，因为其供给域的面积虽然可能大于需求域的面积，但却不一定完全覆盖。同理，当F<0时，表示供给没有满足需求，但供给可能存在某一部分的供给超过了需求。因此，需将契合度和供给程度结果对照分析，如表1所示。

同时，可以计算其供给程度：

表1 契合度和供给程度结果对照表

2 权重分析

2.1 影响因素权重

对于地基基础（D）、主体结构（ZT）、防水工程（F）、保温工程（B）、水电安装（S）、装修工程（ZX）权重确定，比较客观、准确的方法是根据各部分发生质量问题的概率、发生后的损失程度来确定，但在调研过程中发现，6个部分工程质量问题发生后造成的损失难以统计。因此，本研究采用客观加主观评价的方法确定权重。将6个部分权重的影响因子分为3个部分，质量投诉数量、工程造价、质量缺陷相互影响程度。其中，质量投诉数量占比反映其质量问题发生概率；平均工程造价占比可以从金额上反映当发生质量问题时各部分自身可能直接损失的上限；相互影响程度可以反映当某部分发生质量问题时，对其他部分的影响程度。因此，首先对这3个影响因素进行问卷调研，分析其各自的权重。用Santy的1~9标度法对所选结果进行赋值[8]。然后对调研结果形成的平均矩阵A进行归一化处理，得到W，再通过下式进行一致性检验。

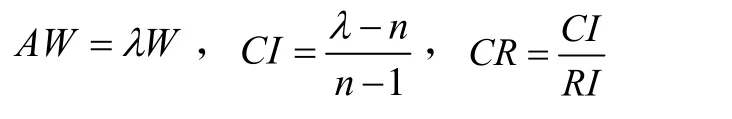
式中，A为调研结果的平均矩阵；W为A归一化后的矩阵；n为矩阵阶数；λ为矩阵A的最大特征根；CI为一致性指标；RI为随机一致性指标，RI的取值如表2所示。

表2 随机一致性指标RI取值表

通过统计、归一化处理和计算得：

结果通过了一致性检验。故质量投诉、工程造价、质量缺陷相互影响程度的权重如表3所示。

表3 影响因素权重

2.2 影响因素取值

（1）质量投诉数量。根据我国 6个省市工程质量投诉的调研统计[9]，这6个部分的质量投诉数量占比如表4所示。

表4 各部分质量投诉数量占比

用Q表示各部分质量投诉数量占比，则：

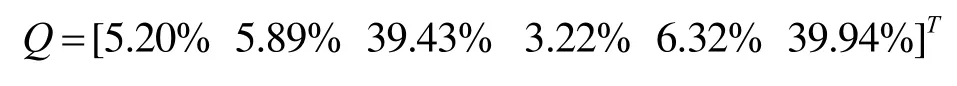
（2）工程造价。由于这 6个部分中，地基基础的变动较大，因为针对不同的地质情况，其地基基础的费用会大幅度浮动。因此，本研究选取了软土、黏土、坚土、砂砾坚土等不同地质条件的6城市，以装修高层住宅工程为例，向其造价站、造价公司进行了调研，调研结果显示，地基基础的造价占比从8%~22%不等，据了解对于海边的部分地区由于其土质情况很差，地基基础的造价占比可能高达40%。因此，在实际工作中，可以根据实际项目或当地的平均水平进行测算，这里主要是做理论研究，对工程质量保险进行验证，因此以调研数据的平均水平为例进行分析，如表5所示。

用C表示各部分工程造价占比，则：

C=[15.28%37.15%2.93% 4.02%14.69%25.94%]T

表5 各部分工程造价占比

（3）相互影响程度。对于 6个部分的相互影响程度进行了专家问卷调研，因为相互影响程度并不是Santy的1~9标度法中Aij和Aji的互为导数关系，并且还存在一方可能不会影响另一方，因此本研究用0~5分表示其影响程度，其中0表示不产生影响，5表示影响严重，0~5之间表示其影响程度从小到大。

设地基基础对主体结构质量的影响程度为b12，主体结构对地基基础质量的影响程度为b21，其余部分相互影响表示方式类似，由此得出这6个方面质量的相互影响程度矩阵：

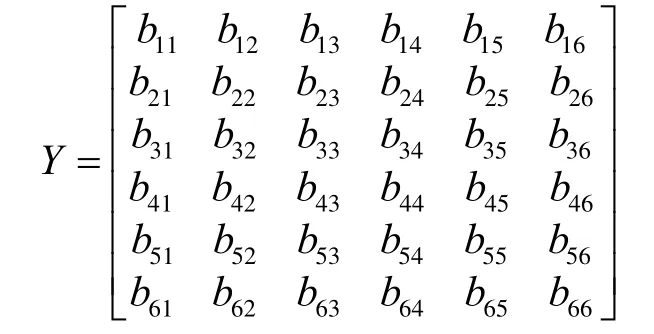
本研究对调研回收问卷的信度进行分析，然后可以通过 SPSS，运用α信度系数进行信度检验，统计结果导入 SPSS，结果显示此问卷的信度达到了0.928，根据α信度系数法，信度在0.8以上表示可信度好，因此问卷结果0.928＞0.8，可信度好。

本研究对问卷平均值进行了统计如表6所示。

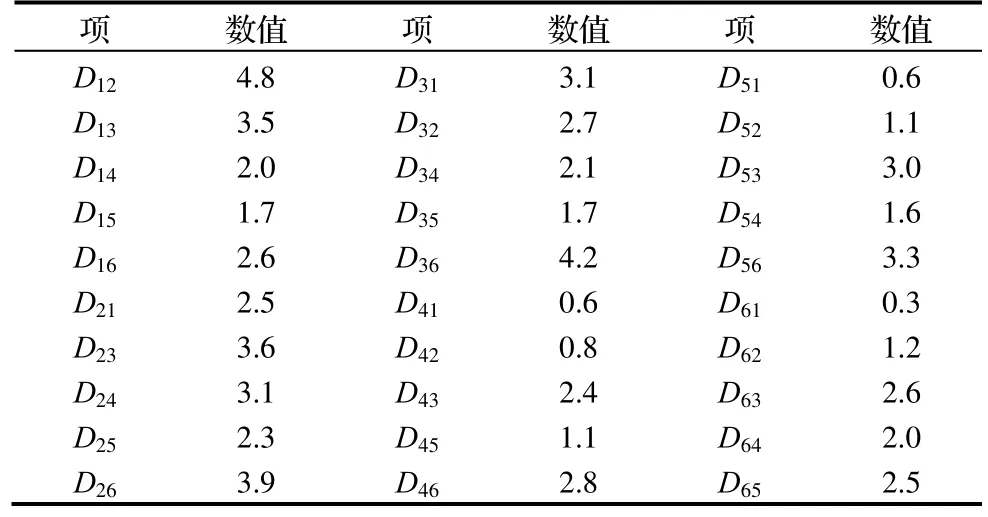
表6 相互影响系数表

因为自身的影响可以根据质量投诉数量和造价的统计进行分析，所以为了避免重复，设自身对自身的影响程度为0，即b11=b22=…=b66=0。形成平均相互影响矩阵：

每个因素对其他因素的影响还需要结合工程造价进行综合分析。因此，各部分对其他部分的影响程度为：

设矩阵E中的每个元素为ei，对此进行归一化处理：

可得这6个部分的相互影响程度如表7所示。

表7 归一化后的工程各部分相互影响程度

2.3 各部分综合权重

通过下式计算6个部分各自的综合权重，结果如表8所示。

式中，PQ表示质量投诉的权重；PC表示工程造价的权重；Pe表示相互影响程度的权重。

表8 工程各部分权重值

3 坐标系设计

在绘制供给域和需求域图像时，6个部分各自对应坐标轴位置的不同，将导致域面积的不同，对计算结构将产生重大影响，因此需要确定6个部分对应的坐标轴。相互影响程度越大的，对应的坐标轴距离越近，反之相互影响越小的，对应的坐标轴距离越远。本研究将6个部分的相互影响程度用箭头粗细表示，以此分析其坐标轴位置。如图2所示。

图2 相互影响程度图像

由于影响是相互的，因此将6个部分相互影响程度两两求和平均，各部分平均相互影响程度如表9所示。

表9 平均相互影响程度排序表

将以上排序大小绘制成关系图，如图3所示。

图3 平均相互影响排序关系图

通过图3发现，排名第1具有绝对优势，因此可以确定，地基基础坐标轴的一侧一定为主体结构坐标轴。此时的排序方案共有：

运用Matlab求得所有排列组合，计算结果如表10所示。

表10 最优方案计算表

由表10可以看出，最小值为34有4种方案，分别为：D-ZT-B-S-ZX-F-D、D-ZT-B-ZX-S-F-D、ZT-D-F-S-ZX-B-ZT、ZT-D-F-ZX-S-B-ZT。

以方案D-ZT-B-S-ZX-F-D为例，6个因素的坐标轴相邻关系为：地基基础—主体结构—保温工程—水电安装—装修工程—防水工程—地基基础，如图4所示。

图4 最优坐标轴方案

4 契合度分析

根据我国6个省市的工程质量投诉数据，按照工程竣工后的实际进行了统计，如表11所示。

表11 工程竣工后质量投诉在工程竣工后的时间分布情况

根据调研统计数据，以及目前国内保险公司在银保监局备案的保险条款，本研究将时间段划分为：竣工后2年内、竣工后第3至第5年间、竣工后第6至第10年间、竣工10年后，并赋予不同的权重，以便与调研分析的质量缺陷发生时间进行契合分析。

但实际使用过程中，部分质量问题发生的时间超过了法律法规规定的保修期，例如部分防水工程、装修工程等发生质量问题的时间超过了保修的5年或2年，这种情况下，本研究认为应当以法律法规规定的保修期为限。因此，这里对于防水工程和保温工程考虑的时间段分为竣工后2年内、竣工后第3至第5年间；对于水电安装和装修工程考虑的时间段为竣工后2年内。

根据质量缺陷发生时间的调研情况，对工程竣工后的时间段进行了赋权，如表12所示。

表12 各时间段权重

（1）需求域。对于需求域的计算，以《建设工程质量管理条例》第四十条的规定为基准，结合各部分的权重和各时间段的权重进行计算。结果如表13所示。

表13 保障期限需求域各时间段权重

通过下式计算需求域各项的坐标值，结果如表14所示。

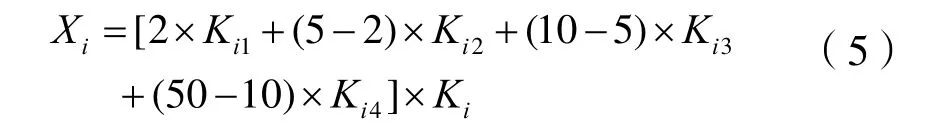
表14 保障期限需求域各项坐标值

形成的需求域图像如图5所示。

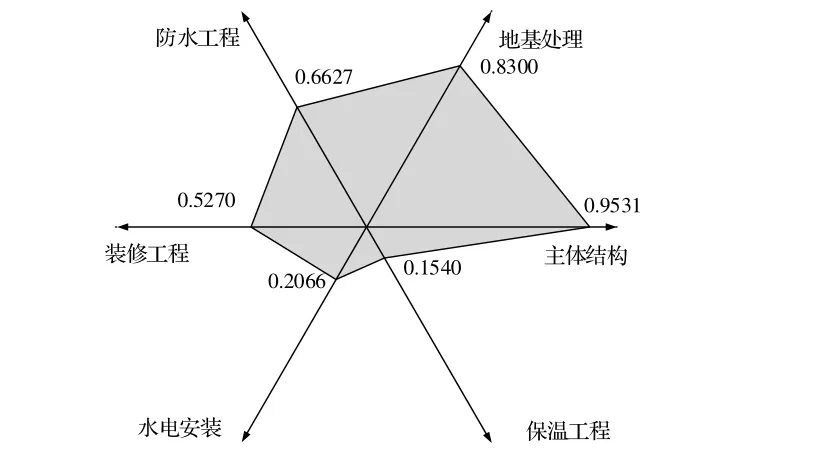
图5 保障期限需求域图像

（2）供给域。对于供给域坐标值的计算，目前国内保险公司在银保监局备案的保险条款中，对于地基基础和主体结构的保险期限为 10年，防水工程和保温工程的保险期限为5年，装修工程和水电安装的保险期限为2年。因此，以保险公司在银保监会报备的保险条款为基准，结合各部分和各时间段的权重进行计算。

参考式（5）计算，供给域各项的坐标值结果如表15所示。

表15 保障期限供给域各项坐标值

形成保障期限的供给域雷达图，如图6所示。

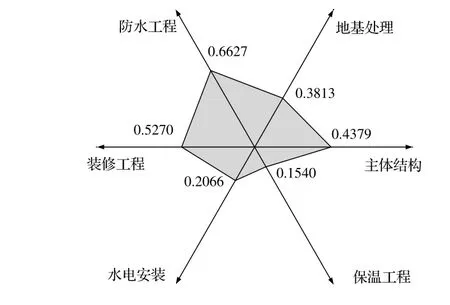
图6 保障期限供给域图像

可知，对于保障期限而言，供给程度达到了需求程度的49.43%，没有任何部分有剩余，距离实际需求差距50.57%。

同理，对于我国现行模式质量保证金留置的契合度进行分析，供给域各项的坐标值结果如表 16所示。

表16 现行质量保证金保障期限供给域各项坐标值

现行质量保证金可以形成保障期限的供给域雷达图，如图7所示。

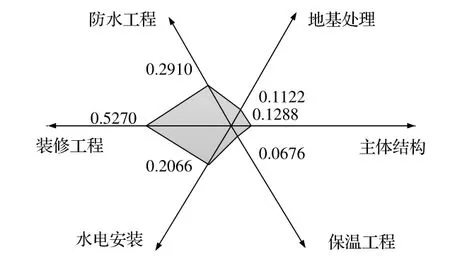
图7 现行质量保证金保障期限供给域图像

通过式（1）、式（2）可得：

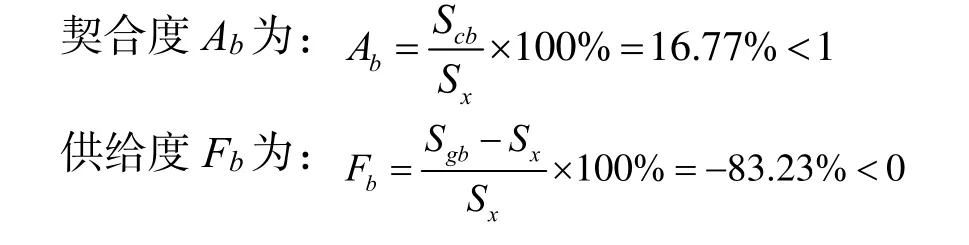
因此，对于现行机制下质量保证金的保障期限而言，其保障程度仅为实际需求的16.77%。质量保证金和工程质量保险的保障期限契合度如表 17所示。可见，虽然工程质量保险的契合度为49.43%，但其已经远远高于质量保证金的契合度16.77%。

表17 保障期限契合度比较

5 结语

本文通过调研和分析，确定了工程质量保险供给需求契合度分析模型的主要因素、权重、坐标轴位置关系，得出了工程质量保险方案的契合度为49.43%，虽然其距离我国的法规规定的保修期（一般房屋建筑 50年）存在差距，但已经保障了几乎一半的风险，且远远高于质量保证金的契合度16.77%，说明工程质量保险对于保障所有权人的合法权益能够比现行制度大幅度提高。