基于有限元方法的复合钢混凝土桥梁热点应力分析研究

(中建七局安装工程有限公司，河南 郑州 450053)

0 引言

大跨度桥梁承担着繁重的交通荷载冲击，桥梁构件易出现疲劳损伤，尤其在焊接构件节点位置，形成疲劳损伤积累[1-2]。因此，对钢混凝土桥梁的关键构件进行局部分析，确定焊接构件名义应力与焊接区域热点应力的关系是十分有必要的[3]。文献[4]对桥梁T型焊接钢管结构进行弯曲试验，确定材料的热点区域位置和应力，给出了热点应力的S-N曲线；文献[5]从材料力学角度出发，采用数值模拟分析了不同构件节点热应力，获得了疲劳损伤的应力幅和损伤部位。国内针对钢梁结构热力分析相对较晚，但也取得了较大成果[6-8]，先后建立了Z向钢的S-N曲线[9]以及热点应力计算公式[10]，同时相关学者通过对管节点疲劳性能分析，得到了加强热点应力区域的补强参数等[11-13]。本文在相关研究的基础上，采用有限元法针对钢-混凝土桥梁热点应力分析，对桥梁疲劳寿命进行合理评估。

1 工程模型构建

1.1 工程背景

青马大桥总长2.2 km，其中主跨1.37 km。桥身分上下两层，上层为双向六车道公路线，下层为铁路线，包括两条单行应急公路和两条铁路。桥塔高206 m，主缆由33 400根直径为5.38 mm的镀锌高强力钢丝构成，每条主缆荷载5.3 t。桥身钢材总重4.9万t，每个桥身重22.7 t，每个鞍座重500 t，桥身由内部桁架和箱型结构构成，通过焊接、铆钉方式将各钢板、薄壁钢梁和杠件连接，图1为大桥结构图。由于桥梁投入运行时间较长，在早期的构件焊接部位中，可能存在早期疲劳裂纹，因此，对该类型焊接热点区域进行动力粘性分析。

图1 大桥整体结构图Figure 1 Overall structure diagram of the bridge

1.2 有限元模型

ABAQUS软件建立青马大桥的三维有限元模型，如图2所示。采用三维2节点空间模型模拟纵向加劲桁架，主索和吊架采用梁单元进行模拟:桥塔多为薄壁多室空间结构，采用空间梁单元进行划分，各单元均按几何尺寸确定。整个模型结构共划分为17 456个单元，7 463个节点。桥梁结构模型性能参数见表1。

图2 青马大桥有限元模型Figure 2 Finite element model of qingma bridge

表1 模型力学性能参数Table 1 Mechanical properties parameters of model类别剪切模量弹性模量泊松比塔顶索鞍重量密度断面直径板桥系统76.922000.3—7 800混凝土桥塔12.6300.2550 0002 400主跨:0.983;边跨:1.097主索—1980.3—7 993

2 结果分析

2.1 动力特性分析

通过建立大桥的数字模型分析桥梁动力特性，得到相应的动力响应频率如表2所示，可以看出，模型计算固有频率和实测值较为接近，最大误差在10%以内，模型计算结果与测试结果一致，表明该数值模型能够很好的反应结构动力特性。

2.2 车载动力响应分析

车辆通过桥梁后，在桥梁构件产生应力循环，为表征车辆通过桥梁时内部构件的响应，按照等效荷载移位原则将外部荷载施加在相应的单元节点，根据虚功原理[14]，移置等效节点荷载与实际荷载外力相等时，则认为二者相互等效，图3列出了经过桥梁时得到的动力响应与实测值曲线，可看出，采用移位响应获得的模拟结果和实测结果相符，满足使用条件。

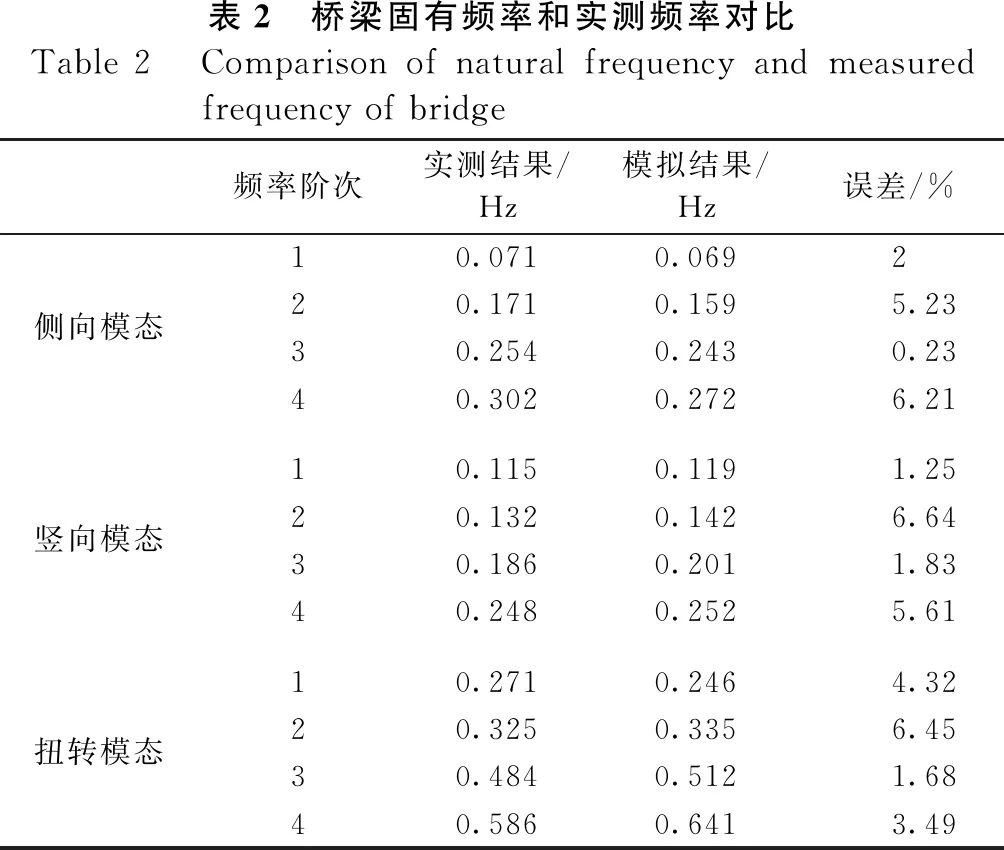
表2 桥梁固有频率和实测频率对比Table 2 Comparison of natural frequency and measured frequency of bridge频率阶次实测结果/Hz模拟结果/Hz误差/%10.0710.0692侧向模态20.1710.1595.2330.2540.2430.2340.3020.2726.2110.1150.1191.25竖向模态20.1320.1426.6430.1860.2011.8340.2480.2525.6110.2710.2464.32扭转模态20.3250.3356.4530.4840.5121.6840.5860.6413.49

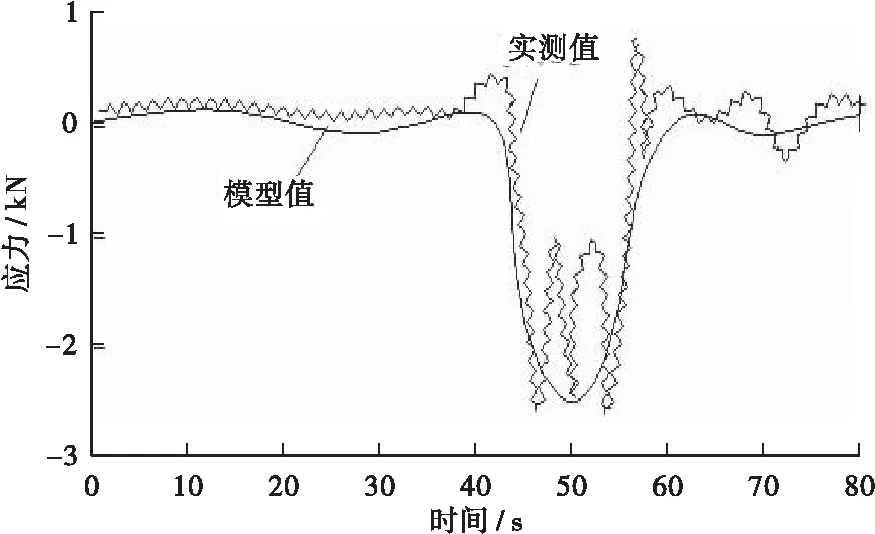
图3 桥梁栋梁响应值对比Figure 3 Comparison of response values of bridge beams and beams

2.3 疲劳危险部位应力分析

相关研究指出，桥梁最危险部位主要发生在交通荷载最外层车道位置[15]。基于此，本文在车辆动态响应下获得图4的应力分布状况，可以看出，桥身主、中间框架最外层车道位置形成了较大的应力集中，容易产生疲劳损伤累计，其他主梁位置也较为类似，靠近桥身最外层车道应力较大，为疲劳危险部位，主框架两侧吊杆悬吊位置几何尺寸变化较大，靠近上层公路外侧框架形成了应力集中点，该处为横向框架和纵向加劲桁架焊接点。

图4 桥身应力分布云图Figure 4 Cloud picture of stress distribution of bridge body

下面列出通过大桥动力和恒载作用下关键构件点局部热点应力。主梁单元整体结构由加劲桁架、主梁横向框架、列车轨道和桥面板组成，其中纵向加劲桁架和主梁横向框架靠近公路外侧，即应力水平较高位置，因此，利用仿真软件建立图5所示的纵向加劲桁架和主梁框架模型。

(a)纵向加劲桁架1

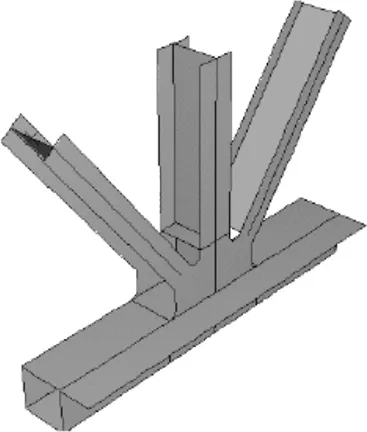
(b)纵向加劲桁架2

(c)主梁框架

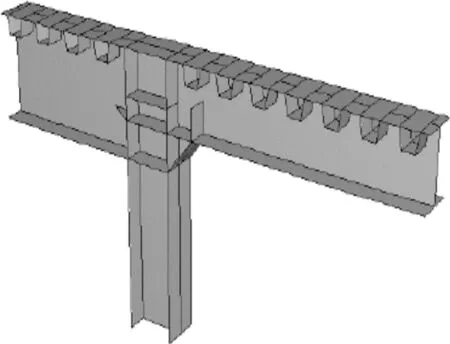
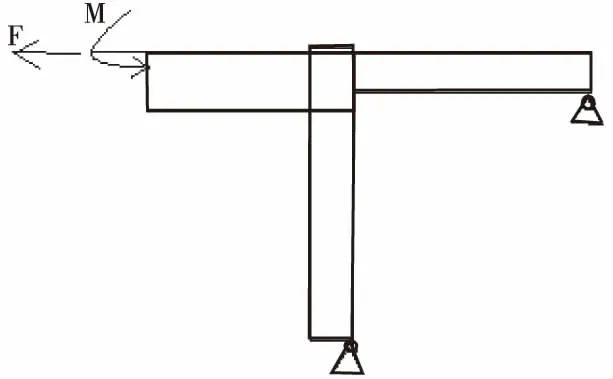
采用软件包中的S4R板壳单元对构件进行网格划分，同时对结构模型施加约束条件，为保证细节边界条件和荷载条件，根据动力响应结果，纵向加劲桁架上下弦杆各向位移均较小，因此在加劲桁架竖立柱上下弦侧施加一个位移边界条件，斜腹杆上下弦杆一侧施加内弯矩和轴向力，主梁竖立柱和横梁一端施加位移边界条件，靠近高速公路外侧横梁施加轴向力和内弯矩。图6为三类典型焊接节点荷载条件。

2.4 热点应力分析

图7为根据表3中纵向桁架细节的荷载组合获得的焊趾附近热应力云图。可以看出，在工字斜撑和上薄壁梁焊接部位产生纵向加劲桁架最大应力，在高速路外侧梁腹板连接处产生主梁桁架最大应力，各构件最大应力区大都集中于构件焊接点位置，即构件的热点区域，是疲劳裂纹造成形成区。

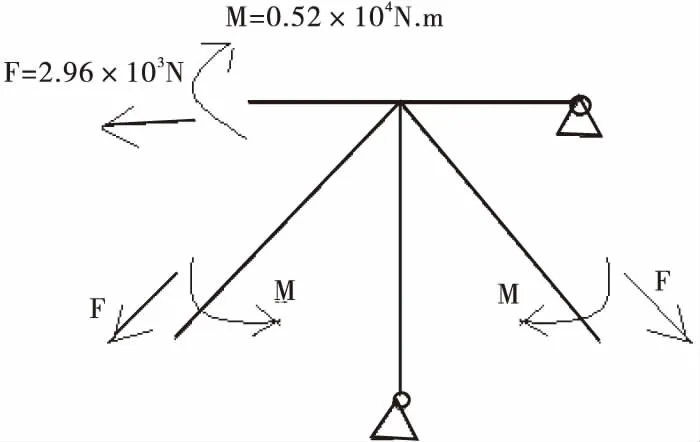
(a) 纵向加劲桁架1

(b) 纵向加劲桁架2

(c) 主梁框架细节

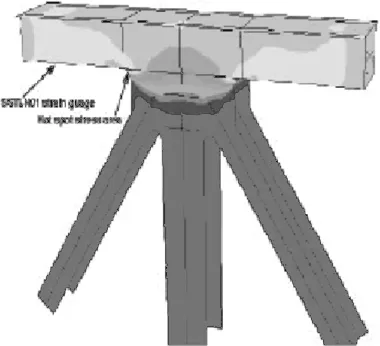
(a)纵向加劲桁架细节1

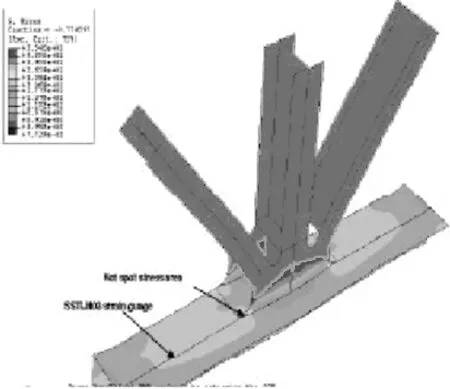
(b)纵向加劲桁架细节2

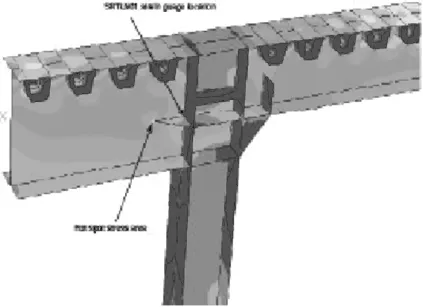
(c)主梁框架细节

根据局部有限元分析结果，得到三类主梁节点焊接区热应力集中系数，见表3所示。比较图7和表3可看出，纵向加劲桁架1、2和主梁中间框架几何结构复杂处产生应力集中。工字型截面斜腹杆和上弦杆、盖板连接部位产生较大的应力。

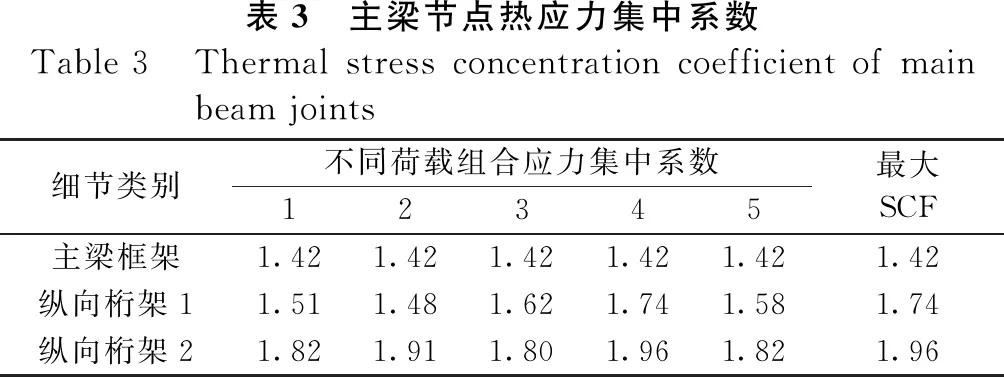
表3 主梁节点热应力集中系数Table 3 Thermal stress concentration coefficient of main beam joints细节类别不同荷载组合应力集中系数12345最大SCF主梁框架1.421.421.421.421.421.42纵向桁架11.511.481.621.741.581.74纵向桁架21.821.911.801.961.821.96

3 疲劳损伤积累分析评价

3.1 热点细节疲劳损伤

对青马大桥三维有限元动力分析表明主梁靠近高速路外层框架应力较大，钢箱梁主、中框架最外层属于疲劳危险区，其他位置主梁应力分布区被认为是疲劳危险部位，为进一步分析交通荷载作用下纵向加劲桁架细节的疲劳损伤累积演化过程，采用全耦法分析加劲桁架细节疲劳损伤累积。本文采用耦合疲劳损伤材料模型[16]，加劲桁架细节模型的网格划分和位移边界条件同上节所示。

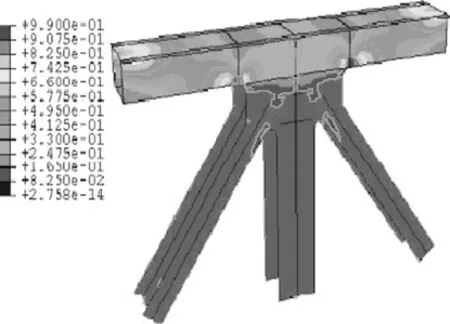
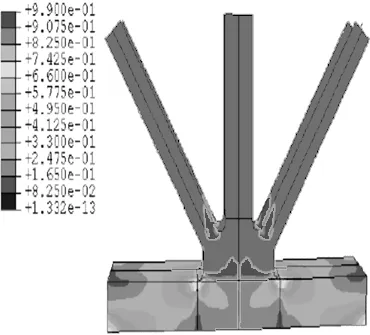
图8和图9为加劲桁架细节疲劳损伤规律。可以看出，细节1的早期最大疲劳损伤累值出现在上下弦对角撑、盖板连接处，与上节分析中局部最大应力位置相同，这主要是因为应力和疲劳损伤间存在的一定函数关系[5]。同时，细节1、2疲劳损伤表现出典型的局部性，损伤累计主要集中于上下弦杆和对角撑、盖板连接位置，当损伤累计到一定程度时，形成疲劳裂纹区，而初始裂纹一旦形成将很快扩展，并最终发生疲劳裂纹破坏，本节疲劳寿命是指结构早期裂纹形成时间点。

3.2 疲劳损伤累积评价

为进一步评价纵向加劲桁架细节疲劳损伤累积情况，定义构件平均损伤形式为[17]：

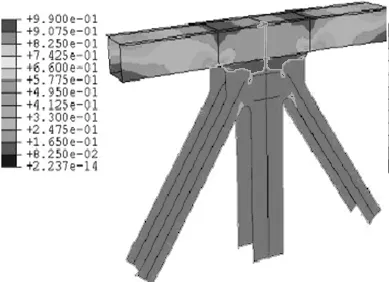
(a)80 a

(b)120 a

(c)160 a

(a)80 a

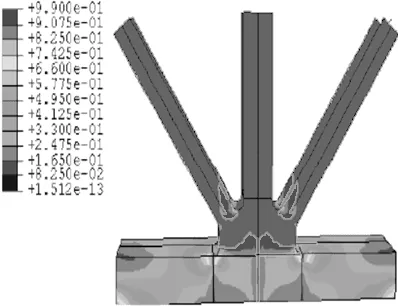
(b)120 a

(c)160 a

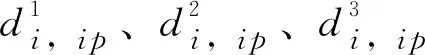
分别采用高周疲劳损伤演化方程[18]及线性米勒准则[19]获得构件内损伤演化规律。图10为构件疲劳寿命曲线。可以看出疲劳损伤累积表现为标准的线性米勒曲线关系，而高周疲劳损伤得到的疲劳损伤累积在初始阶段损伤增幅较小，到了后期增幅速度明显加快。

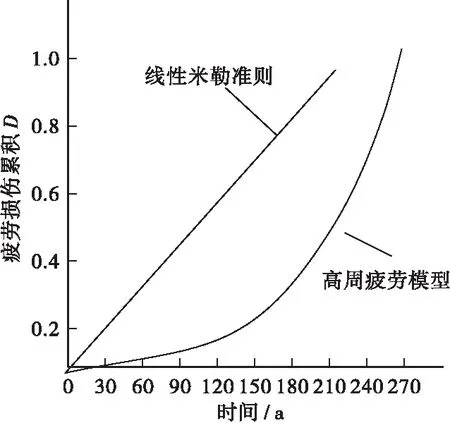
图10 不同算法的构件疲劳寿命曲线Figure 10 Fatigue life curves of components with different algorithms

表4给出了两种计算方法获得的构件疲劳寿命结果。采用线性米勒准则较高周疲劳模型获得的构件疲劳寿命要小，表明实际工程中，基于线性米勒准则得到的构件寿命评估具有更高的安全系数和安全裕度值，这在进行构件疲劳设计过程中是合适的，但是对于长期服役后的结构进行疲劳损伤累计评价并不理想，由于疲劳损伤早期累积损伤变化率较小，后期变化率较大特点，而采用线性米勒准则将这种疲劳损伤累积简单的等效为线性关系[20]，夸大了疲劳损伤的早期积累，而降低了后期疲劳损伤的快速扩张状况。

表4 不同分析方法获得的构件焊缝疲劳寿命Table 4 Fatigue life of weld of components obtained by different analysis methods构件高周疲劳模型/a线性米勒准则/a细节1245185细节2240190

4 结论

a.采用大桥有限元模型进行动力特性分析，模型计算固有频率和实测值最大误差在10%以内，计算的动力特性和设计测试阶段特性相符。

b.纵向加劲桁架细节热点应力区域出现在上下弦杆与对角撑、盖板连接处，与焊缝构件疲劳损伤最大值出现位置一致。主梁框架热应力区域出现在靠近公路外侧梁腹板连接处。

c.线性米勒准则获得的疲劳损伤累积呈线性，计算结果偏于安全，适合于结构疲劳设计；高周疲劳损伤初期损伤率增长较慢，后期较快，适用于在役结构疲劳寿命评价。