斜拉索腐蚀损伤下斜拉桥体系可靠度研究

鲁乃唯

(1.长沙市轨道交通集团有限公司，湖南 长沙 410007;2.长沙理工大学 土木工程学院，湖南 长沙 410114)

经过30多年的发展，我国的桥梁建设取得了瞩目成就，特别是在大跨缆索支承桥梁的建设规模与数量方面发展迅速[1]。在缆索承重桥梁的使用过程中，主缆、拉索、吊索等关键受拉构件受环境腐蚀、疲劳损伤、振动等因素导致强度下降现象较为普遍，威胁桥梁运营安全[3]。事实上，一方面，缆索(或拉吊索)截面面积小，布置在梁体外部，且长期处理高应力状态，在外层防护套与防腐涂层耐久性不足的情况下，缆索易腐蚀；另一方面，车辆超载导致缆索构件疲劳损伤严重，疲劳裂纹的出现又加速了缆索的腐蚀进程。斜拉索的设计寿命为30 a，然而受到腐蚀与疲劳损伤等因素的影响，斜拉索的实际使用年限普遍在16 a以内[4]。在拉索腐蚀与疲劳损伤普遍存在且持续劣化的情况下，研究腐蚀后的力学性能及其对桥梁结构安全的影响具有重要的工程指导作用。

针对斜拉索的腐蚀损伤问题，目前研究工作主要是从现场检测、室内盐雾腐蚀试验和数值模拟等方面探索其腐蚀机理与规律。与常规的金属腐蚀不同，拉索腐蚀表现出应力腐蚀现象[5]。在钢丝腐蚀后的力学性能方面，国内外学者开展了大量研究。Faber等[6]最早通过腐蚀斜拉索的力学性能试验研究，基于串并联模型研究了在役斜拉索的抗拉强度与疲劳强度概率模型。李慧等[7]对服役18 a的平行钢丝斜拉桥进行了力学性能试验研究，拉索弹性模量变化相对较小，而强度有所下降，极限应变降低约11%，腐蚀钢丝没有明显紧缩。XU等[8]利用串-并联体系研究了在假设腐蚀分布的拉索横截面处的力学行为。贡金鑫等[9]研究了不锈钢钢丝腐蚀后的可靠指标变化趋势。张可心等[10]研究了拉索损伤对某双塔双索面斜拉桥的挠度和索力等静力性能的影响规律。

斜拉索作为斜拉桥的主要承重构件，为主梁提供多点弹性支承，增加了结构体系的超静定性与安全性。国内外诸多学者基于结构体系可靠度理论研究了斜拉索对斜拉桥结构体系安全的影响。BRUNEAU[11]采用体系可靠度方法分析斜拉桥结构体系的力学行为，发现9种潜在的失效模式。LIU等[12]采用更新支持向量方法分析大跨度斜拉桥结构体系的主要失效路径，认为大跨度混凝土斜拉桥的首要失效路径是边跨斜拉索失效导致主梁索塔弯曲失效。鲁乃唯等[14]提出了斜拉桥体系可靠度分析的高效智能算法。

综上所述，目前在斜拉索的腐蚀损伤机理和斜拉桥体系可靠性分析研究方面取得了一定的成果。然而，现有的研究成果多集中于斜拉索腐蚀疲劳损伤的确定性研究，缺少考虑斜拉索腐蚀疲劳损伤的概率研究。在斜拉桥体系可靠度评估中缺乏研究斜拉索腐蚀损伤对斜拉桥体系可靠度的影响。

本文基于结构体系可靠度理论，采用串并联系统建立斜拉索腐蚀损伤的抗力退化概率模型，提出考虑斜拉索腐蚀损伤的斜拉桥体系可靠度分析方法。最后，以混凝土斜拉桥为例应用上述斜拉索抗力退化概率模型与斜拉桥体系可靠度分析方法，评估该斜拉桥的时变体系可靠度指标，为换索决策提供理论依据。

1 斜拉索腐蚀损伤下抗力概率模型

1.1 斜拉索的串并联模型

斜拉索通常采用镀锌高强钢丝或钢绞线，外层为高密度聚乙烯(HDPE)护套，由于HDPE层防护套的老化、钢丝索防腐层失效、灌注水泥浆不密实等原因，酸性雨水或水蒸汽与钢丝发生微电池催化式反应，导致钢丝腐蚀，并呈径向扩展。以平行钢丝为例，本文建立斜拉索腐蚀疲劳损伤下的拉索强度退化概率模型。

对于一根拉索的强度概率模型，目前较为成熟的模拟方法是采用Weibull概率分布函数来表示：

(1)

式中:z是斜拉索的强度，λ、u、k分别表示Weibull分布函数的尺度、位置和形状参数。由于该函数未考虑斜拉索的腐蚀损伤效应，则可视为斜拉索腐蚀后的某一未腐蚀段的拉索强度概率模型。因此，可将斜拉索在腐蚀位置将拉索进行离散处理，处离散单元均为未腐蚀的拉索，而单元节点处则为腐蚀点。

采用如图1所示的串并联系统将一根斜拉索离散成若干单元，单元与单元之间由串联方式模拟斜拉索的长度效应，单元与单元之间的并联模式模拟拉索的数量效应。刚拉索的腐蚀损伤则以斜拉索的单元长度L0来考虑，即当斜拉索损伤严重时拉索单元长度较短；而拉索腐蚀损伤较轻时，则拉索单元长度较长。

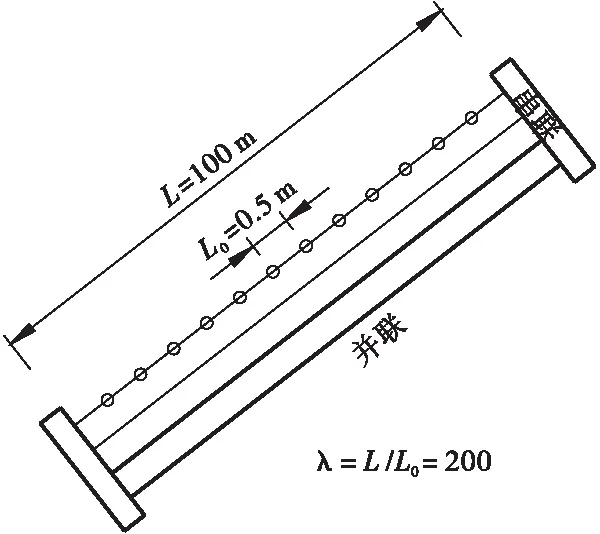
图1 斜拉索离散单元的串并联模型Figure 1 Series-parallel model of discrete cable elements

为了描述该串并联模型的有效性，采用Faber等的腐蚀拉索强度试验数据为依据，分析拉索数量与长度效应对斜拉索强度的影响。根据Faber等的研究结果，在斜拉索钢丝的数量足够大的情况下，平行钢丝索的强度服从正态分布，拉索强度拉值可表示为:

E(n)=nx0[1-Fz(x0)]+cn

(2)

假定拉索钢丝样本数量是30个，样本极限强度均值σu=1 788.7 MPa，Weibull模型的分布参数k=72.62，假定比例因子λ=L/L0=1, 3, 10，则拉索钢丝数量从10变化至300的斜拉索强度退化模型如图2所示。

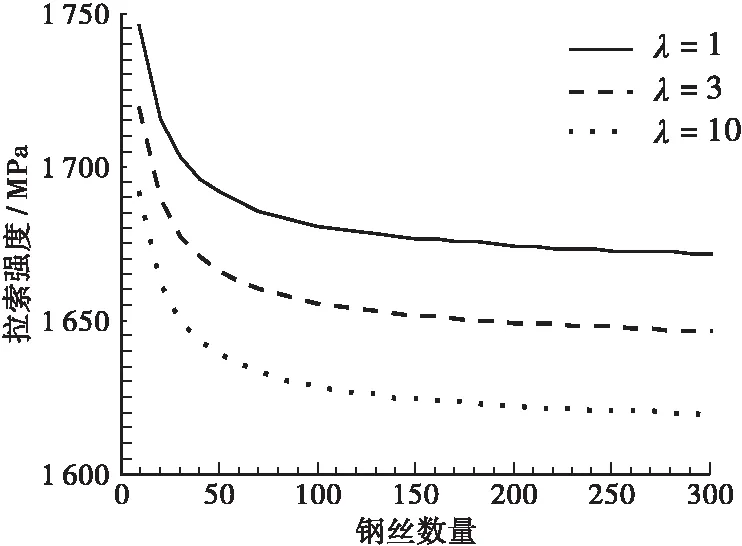
图2 钢丝数量效应对斜拉索强度的影响Figure 2 Influence of number of cables on the cable strength

由图2可知，斜拉索强度随着钢丝数量的增加有所下降，且随着损伤因子λ的增加而下降。当λ=10时，拉索数量由10增加至300导致斜拉索强度下降4.3%。在一根斜拉索的钢丝数量为300的情况下，损伤因素λ由1提高至10将导致斜拉索强度下降3%。

1.2 斜拉索强度的概率模型

如图2所示的拉索腐蚀强度退化模型未考虑斜拉索强度的随机性，因此，需研究斜拉索强度退化的概率特征。标准差可表示为：

(3)

文献LI[7]对运营20 a的69根腐蚀平行钢丝索与13根未腐蚀平行钢丝索的疲劳试验研究，采用样本长度0.5 m的钢丝，钢丝样本的概率密度曲线如图3所示。基于文献[12]的钢丝样本的强度概率模型，考虑长度为232 m，数量为n=243根的某斜拉索束。该斜拉索设计强度为σb=1 766 MPa，则由式(2)可得到该斜拉索的强度退化概率模型。

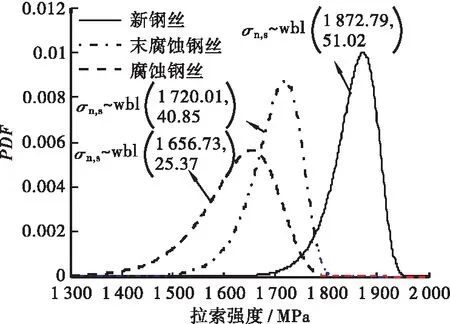
图3 钢丝样本的强度概率密度曲线Figure 3 Probability density curves of strength of cable specimen

由图4可知，拉索运营20 a后，腐蚀拉索和未腐蚀拉索的疲劳强度相对新斜拉索的强度分别下降32%和13%，而标准差下降幅度不到2%。由此可知，拉索数量和长度导致的拉索强度变异系数可忽略不计。

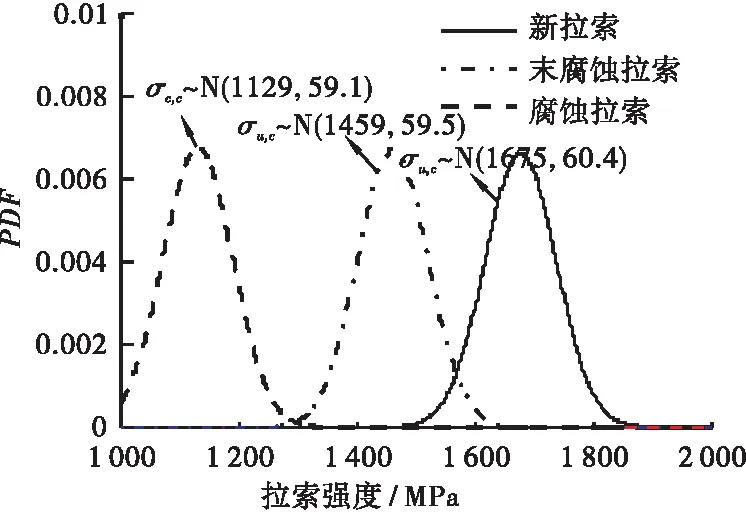
图4 某斜拉索的强度概率模型Figure 4 Probability model of strength of a cable

2 考虑斜拉索抗力退化的斜拉桥失效路径搜索方法

结构可靠度常用的分析方法是一次二阶矩法、Monte Carlo抽样方法、响应面法等，但并不适用于斜拉桥的体系可靠度分析。与常规梁式桥的可靠度分析相比，斜拉桥具以下特点：首先，斜拉索的垂度效应与梁柱效应导致结构的非线性行为显著，需要构建复杂的结构功能函数；其次，斜拉桥的超静定次数较高，若干拉索失效并不致使结构体系失效，桥梁结构体系表示显著的失效路径特征；最后，斜拉索腐蚀后的抗力退化显著(见图4)。在上述因素的影响下，常规的结构可靠度分析方法计算精度与效应较为低下。鉴于此，本文针对斜拉桥体系可靠度分析中的失效路径搜索问题，提出一种响应面更新方法，用以捕捉斜拉桥的非线性效应、斜拉索强度退化对结构失效路径的演化等。

基于响应面更新方法的斜拉桥失效路径搜索与体系可靠度计算的流程如图5所示，其中关键步骤如下：

a.通过结构的参数敏感分析，筛选影响结构主要失效模式的关键随机变量，例如荷载、拉索弹模、混凝土容重等。

b.采用二次序列响应面方法拟合随机变量与桥梁关键构件响应之间的函数关系，由Monte Carlo抽样方法计算各关键构件的可靠指标。

c.采用β约界方法搜索关键构件的失效单元，并对失效单元处理，例如，脆性破坏的构件删除失效单元，塑性构件则增加塑性铰。

d.基于斜拉桥新结构更新响应面，重复步骤b和c，直至结构体系失效，再构建结构的失效树。

e.考虑斜拉索腐蚀导致的抗力退化概率模型，更新斜拉索参数，返回步骤a。

f.计算时间达到斜拉索设计年限(20～30 a)结束。

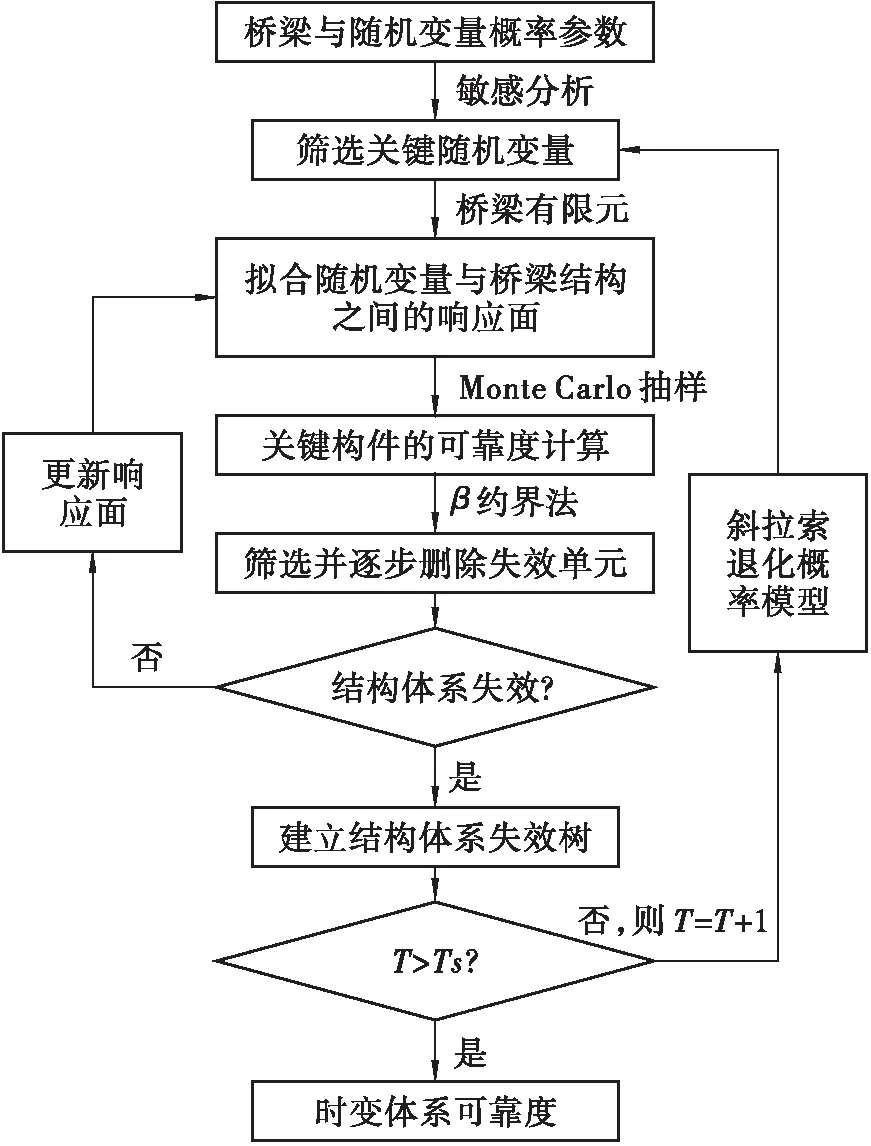
图5 考虑斜拉索抗力退化的斜拉桥失效路径搜索方法Figure 5 A method for searching failure sequences of cable-stayed bridges considering cable strength degradation

采用如图5所示的更新响应面方法分析斜拉桥体系可靠度的优势在于：

a.由响应面函数拟合斜拉桥结构的荷载响应，捕捉到拉索垂度、梁柱效应、大变形等非线性效应。

b.采用β约界方法搜索潜在失效单元，并以更新响应面的方法拟合单元失效后的新结构功能函数，捕捉到单元失效后结构体系的特性。

c.考虑斜拉索抗力退化，再次更新斜拉桥有限元模型，重新开展失效构件的筛选分析，虽然计算较为繁琐，但可捕捉到斜拉索抗力退化对结构体系可靠度的影响。

3 斜拉桥的时变体系可靠度分析

3.1 Brotonne斜拉桥概况

BRUNEAU[11]分析了图6中所示的小跨径斜拉桥的结构体系可靠度的影响。该斜拉桥为独塔，每侧有2根斜拉索，在主梁及索塔上的拉索锚固件之间的距离为30 m。更多关于材料、截面特性及功能函数的细节可参见BRUNEAU[11]。本算例在此基础上研究了斜拉索强度退化对该斜拉桥失效路径及体系可靠度的影响。

图6 Brotonne斜拉桥的尺寸及失效模式Figure 6 Dimensions and failure modes of brotonne cable-stayed bridge

3.2 失效树的构建

在此算例分析中，结构力学行为假设为线性和弹性(与BRUNEAU的方法一致)。拉索断裂失效为脆性破坏，混凝土主梁和桥塔被认为是塑性的，通过塑性破坏机理定义结构体系的失效。塑性断裂机理由塑性铰位置和塑性能力确定，常由弯曲失效控制。潜在失效位置如图6所示，该塑性铰的出现也是该斜拉桥体系失效的标志。主梁的G1～G11点和索塔的T1、T2点受弯曲失效控制，拉索的C1～C4构件受强度失效控制。

从体系层面的角度来看，如拉索断裂，直接删除拉索，并重新评估新结构的承载能力。如果发生主梁或索塔的弯曲失效，则在发生弯曲失效的位置添加塑料铰。由于结构刚度和抗力每个阶段都在改变，这意味着剩余的结构构件将重建为新的结构体系。当过程结束时，失效路径的发展将在构件失效的情况下停止，最终构件的失效概率是非常高的。为节省计算量应停止该搜索过程，即便该结构仍具备一定的承载能力。由于BRUNEAU已提供了明确的极限状态函数，因此，ASVR方法在此不用作近似及更新桥梁模型，而采用图2所示的拉索的强度系数直接更新极限状态函数。基于上述假设，构建了拉索未产生抗力退化和拉索产生20%抗力退化的失效树。图7给出了评估的结果。

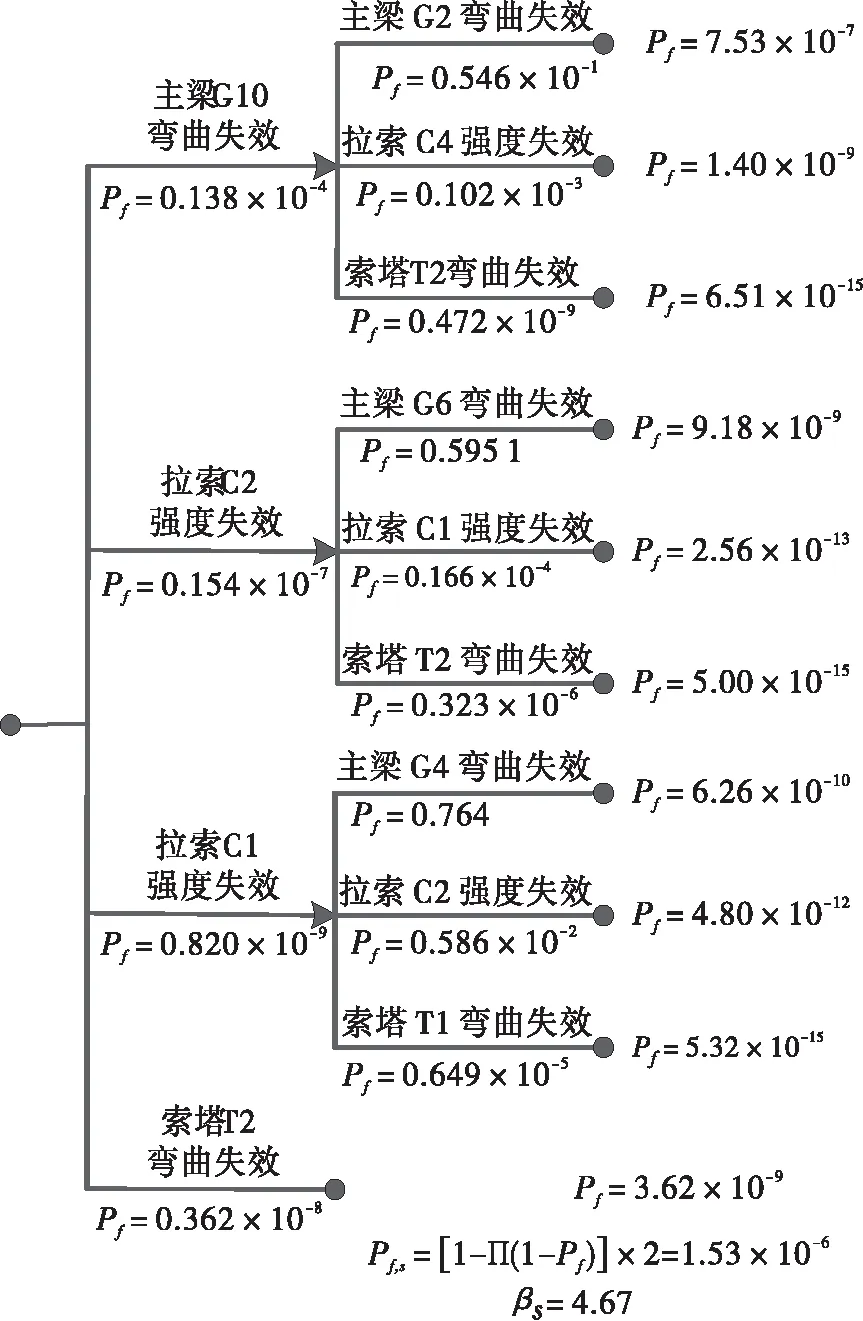
(a) 拉索未产生抗力退化(b) 拉索抗力退化系数为20%

从图7可以得出以下结论：①随着拉索强度降低20%，C2拉索的失效概率从0.154×10-7急剧下降至0.243×10-4。②主要失效路径发生变化，最初主要失效模式在G10和G2处的塑性铰处开始，拉索性能退化导致C2拉索失效作为主要失效路径的开始，随后是G6梁的弯曲失效。最后，结构体系的失效概率从1.53×10-6增加至44.6×10-6。 综上所述，拉索抗力退化不仅降低了拉索的可靠性，而且对结构主要失效模式和体系可靠度有着显著影响。

3.3 体系可靠度评估

为了研究拉索抗力退化对斜拉桥体系可靠度的影响，利用图1所示的拉索性能退化模型来更新和重新评估体系的可靠性。图8给出了桥梁20 a服役期的时变体系可靠度。

图8 考虑拉索抗力退化影响的斜拉桥体系可靠度指标Figure 8 System reliability index of the cable-stayed bridge considering cable strength degradation

从图8可看出，与图2所示的拉索强度模型相比，体系可靠指标具有相似而不同的趋势。相似的是考虑疲劳和腐蚀共同作用与仅考虑疲劳作用下，体系可靠指标均降低。不同的是疲劳和腐蚀共同作用下的体系可靠指标从服役期的第13年开始快速下降。这种现象可通过图7所示的失效树来解释，其中主要失效模式由在拉索强度降低到临界值时的拉索失效转变为结构体系失效。由此得出，在服役期的13 a内，疲劳和腐蚀共同作用下拉索失效的概率大于G10梁弯曲失效的概率，这是之前的主要失效模式。因此，持续的拉索抗力退化导致主要失效模式从梁到拉索的变化，这种变化亦导致体系可靠指标快速下降。

4 结论

a.建立了考虑疲劳损伤和腐蚀作用的拉索抗力退化概率模型，提出了考虑拉索抗力退化的斜拉桥体系可靠度分析方法， 验证了该分析方法的可行性。

b.疲劳和疲劳腐蚀效应共同作用下的拉索在20 a服役期内的强度系数分别为0.928和0.751，疲劳效应的曲线接近线性，然而疲劳腐蚀效应的曲线是非线性，腐蚀作用是导致拉索强度快速降低的重要因素。

c.构建了斜拉桥在不同服役阶段的失效树，分析了斜拉索退化对该斜拉桥体系可靠度的影响。斜拉索抗力退化将导致斜拉桥主要失效路径变化，主梁索间距为30 m的斜拉桥在服役期的13 a，主要失效模式从由主梁弯曲失效转移至斜拉索强度失效，导致后期的结构体系可靠指标快速下降。