动应变测量在桥梁动挠度识别中的应用分析

(1.河南省交通运输厅 公路管理局，河南 郑州 450016 ；2.河南鼎智工程咨询有限公司，河南 郑州 450045)

1 概述

桥梁是交通网络中重要的组成部分，它的使用年限和使用质量对人们的生活至关重要。通常情况下，大型的较重要桥梁设计使用100 a，但是由于桥梁设计上的考虑不足、使用上的不可抗力因素影响、维修养护阶段的差异性造成桥梁的实际使用年限良莠不齐，很多达不到100 a。截止2005年，美国桥梁有700 000座，有196 000座存在问题；截止2016年我国桥梁有600 000座，其中有150 000座存在问题，这些存在问题的桥梁，需要定期修复，修复费用昂贵，同时严重影响桥梁的安全性和稳定性，成为很多安全事故的根源，如图1所示。

(a) 南门长江大桥

(b) 西安陇海铁路灞河铁路大桥

桥梁检测是预防和减少事故发生的重要措施，变形是桥梁检测的重要内容，挠度是变形性能的指标之一。动挠度是指桥梁当有车辆等通过，在动荷载的影响下产生振动，使桥梁发生变形，是反应实际运行中的变形参数。所以研究桥梁的动挠度识别很有必要。

直接测量挠度可以使用传统方法进行测量，比如水准仪、百分表等。随着科技进步，出现了新的测量方法，比如GPS法、激光成像法、光电成像法等。此外还有基于应变的间接挠度测量方法。

2 应变模态理论分析

模态是桥梁结构在振动环境下所表现的特性，特性参数有频率、阻尼以及振型。基于研究位移的模态理论对于应力集中等特殊情况的分析不适用，而基于研究应变的模态理论适用范围广泛。

当结构产生自由振动时，可以分解为N个模态，在研究应变模态时用应变向量来表示，根据位移模态向量，通过有限元法、直接换算法等，推导出应变模态向量。有限元法的推导如下：

根据结构中点的唯一关系可以得到：

{δ}1=[P]{a}1

(1)

其中,{δ}1为第i个单元的节点位移列阵;{a}1为代表第i个单元中任意一点的位移列阵；[P]为是位移函数矩阵(一般为多项式函数)。

根据节点位置，可以得到：

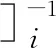
(2)

其中,[A]i为数值矩阵；将式(2)代入式(1)可得：

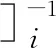
(3)

根据微分，可得:

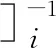
[B]{δ}i

(4)

其中,{ε}i为第i个单元内某一点的应变；[D]为微分算子。

推导出

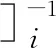
(5)

若单元数为p个，则式(4)可写成:

{ε}=[B]{δ}

(6)

其中,{ε}为个单元内的应变；{δ}为P个单元的节点位移。

考虑连续性，可得：

(7)

通过模型，可以得到:

{ε}=[B][β][φ][Yr][φ]T{Fs}ejax=

(8)

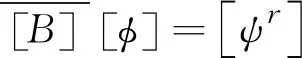
3 动应变模态在识别梁的挠度中的应用

已有文献对简支桥梁进行了研究，本文对连续桥梁进行研究。首先，依据实际桥梁，建立桥梁模型实验；然后应用动应变模态理论，对桥梁模型实验结果进行处理，得到不同情况下实验模型的挠度值；最后，进行实际桥梁验证，分别将不同情况下，实际桥梁的挠度测量值(即精确值)和试验模型的挠度计算值(即计算值)进行对比，验证该挠度识别方法的可行性。

3.1 建立桥梁模型

以实际桥梁为对象，将其按照1∶10的比例进行桥梁实验模型的建立，分析动应变模态在识别梁的挠度中的应用。连续梁桥梁模型的截面为工字型界面，基本参数为：全长10 m，截面积为2.52 cm2，惯性矩为10.8 cm4，高50 mm，以每0.5 m为一个单元，将梁划分成20段，模型如图2所示。

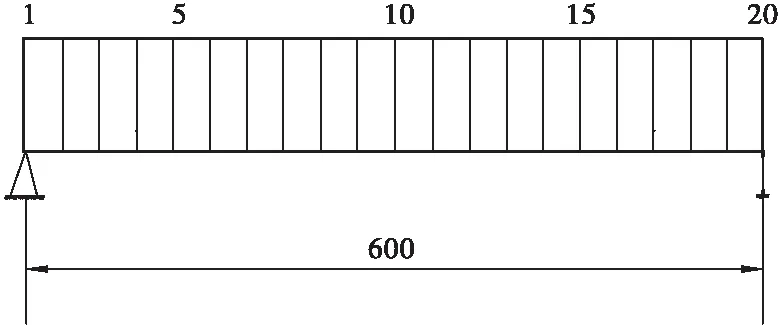
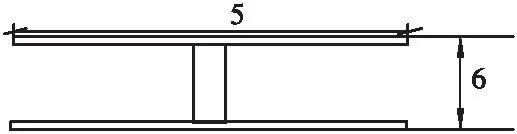
图2 桥梁模型结构

3.2 求解应变模态振型

研究应变动态模型，主要研究其主振型的应变模态振型，由于研究的连续梁跨数为两跨，其主要的主振形为前三阶。研究步骤分以下3步：

a.通过白噪声激励试验，获取梁的应变，白噪声的参数为力的均值为0，标准差为0.25g，持续作用时间20 s，通过应变传感器收集数据。

b.通过互相关函数法，得到应变模态振型。

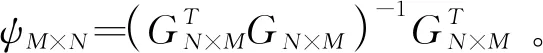
c.通过有限元结果验证，对比结果见图3，从图中可知，根据一阶振型得到的模型的精度较高。

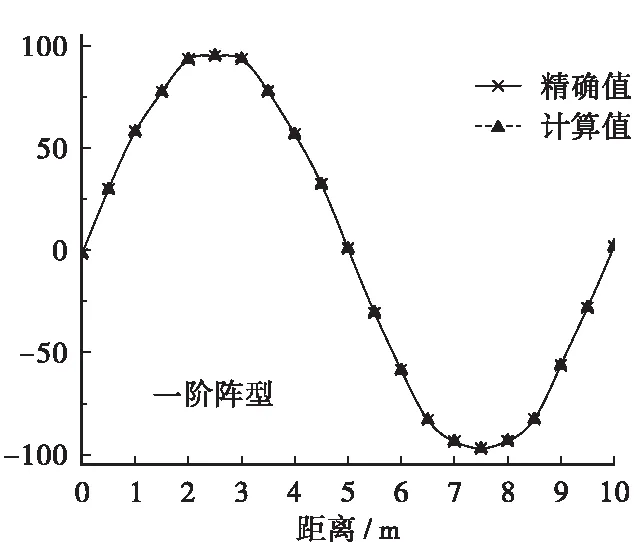
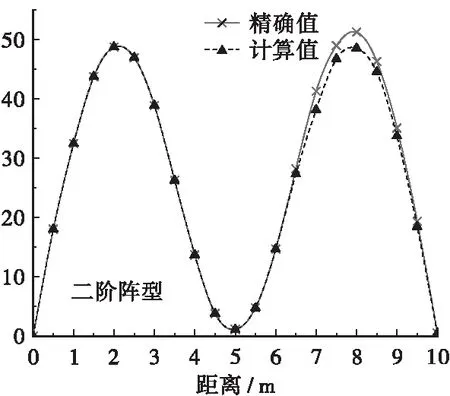
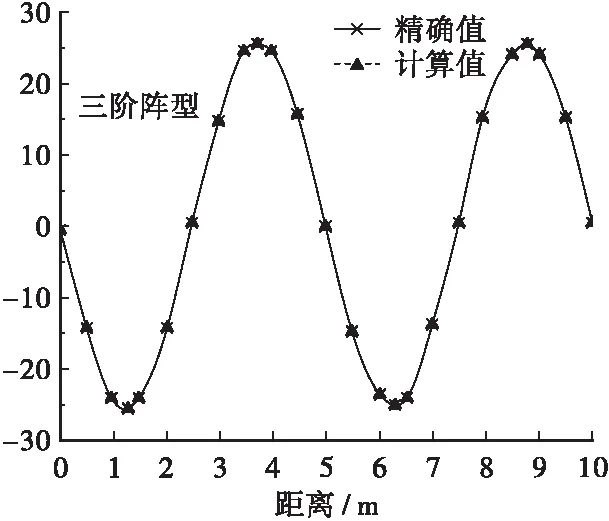
图3 计算结果与有限元计算结果对比

Figure 3 Comparison of calculation results with finite element calculation results

3.3 脉冲荷载下梁动挠度识别与实桥验证

动挠度识别通过给梁施加脉冲荷载，采用数值模拟对结果进行处理。试验时，对梁左端跨的四分之一处施加100 N的荷载，持续作用0.03 s；对梁右端跨的二分之一处施加100 N的荷载，持续作用0.03 s。通过应变感性器收集数据，为了使数据具有一定的价值，布置如图4所示。由图4可知，在左端跨和右端跨分别设置三个点，在左端跨设置的测量点的间隔为1.25 m，分别命名为1、2、3，第一个测量点与最左端的距离为1.25 m处，以此类推；在右端跨设置的点的间隔为1.25 m，分别命名为Ⅰ、Ⅱ、Ⅲ，第一个测量点与最左端的距离为6.25 m处，以此类推。

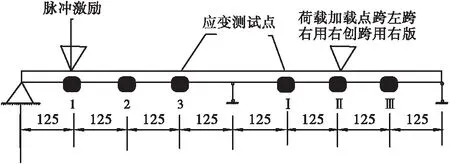
图4 脉冲激励示意图Figure 4 Schematic diagram of pulse excitation

通过施加荷载，测得各个应变点的应变，收集应变数据，对数据进行处理，得到各个点的动挠度，为了保证挠度计算的有效性，对比实际桥梁测量后的挠度精确值和实验模型识别后的挠度计算值基本一致，二者的吻合度越高表明挠度计算精确度越高，结果越具有参考性。通过对测试数据进行分析，得到结果如图5所示，图5(a)为根据测试点1、2、3得到梁左端的挠度值与测量值之间的对比图，可以直观的看到精确值和识别值之间基本重合，识别结果有效；图5(b)为根据测试点1、2、3得到梁右端的挠度值与测量值之间的对比图，可以直观的看到精确值和识别值从开始到0.5 s的过程中，二者的值相差较大，挠度计算结果的有效性不足；图5(c)为根据测试点Ⅰ、Ⅱ、Ⅲ得到梁右端的挠度精确值与识别值之间的对比图，可以直观的看到精确值和识别值之间基本重合，识别结果有效。为了使测量结果有效，精确值和识别值基本一致，当测量某跨的挠度时，应在测量跨处布置测量点，进行数据收集。

3.4 振动荷载下梁动挠度识别与实桥验证

为了使梁在震动荷载下的挠度识别可以在实际工程中应用，以地震荷载作为振动荷载模拟进行梁的动挠度试验。试验时，对梁施加的荷载为地震波，地震波采用EL CENTRO地震波，在梁左端的动挠度采用测点1、2、3的动应变数据识别，在梁右端的动挠度采用测点Ⅰ、Ⅱ、Ⅲ的动应变数据识别，梁左端的测试结果如图6所示，由图可知，

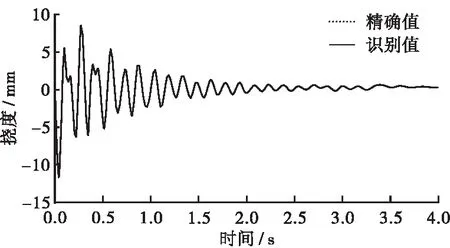
(a) 根据测试点1、2、3得到梁左端的挠度精确值与识别值之间的对比图

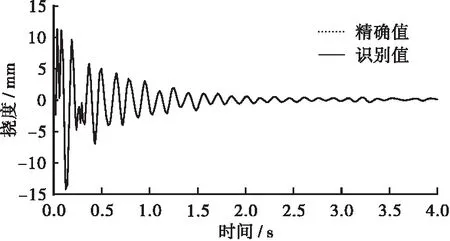
(b) 根据测试点1、2、3得到梁右端的挠度精确值与识别值之间的对比图

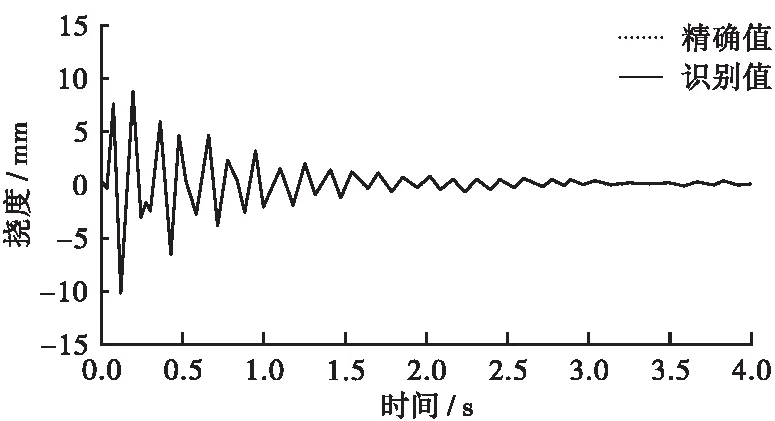
(c) 根据测试点Ⅰ、Ⅱ、Ⅲ得到梁右端的挠度精确值与识别值之间的对比图

Figure 5 Comparison of the exact value of deflection and the identification value

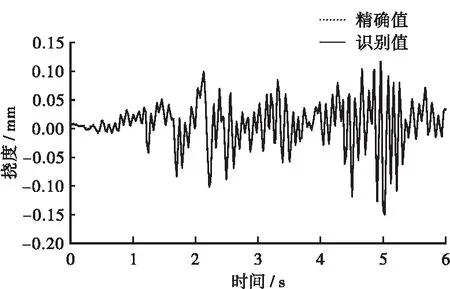
图6 振动荷载作用下，梁挠度精确值与识别值之间的对比图Figure 6 Comparison between the exact value of the deflection of the beam and the identification value under the vibration load

EL CENTRO地震波作用下，实际桥梁测量后的挠度精确值和实验模型识别后的挠度计算值基本一致，本文采用的挠度识别方式准确，精确度较高。

4 结论

通过本文研究，得到：

a.通过分析介绍位移模态理论与应变模态理论的异同点，以及应变模态理论，在此基础上，提出了互关函数在梁动挠度识别中的应用，并且通过试验模型进行应用，利用实际桥梁验证挠度识别方法具有一定的可行性。

b.将桥梁模型分段，每跨布置测量点，采用应变传感器进行测试，通过对梁施加脉冲荷载，对实验数据分析处理得到挠度识别值，经过实桥数据对比，得到在脉冲荷载下，应在测量跨处布置测量点，进行数据收集，这样可以提高试验结果的精度。

c.通过对梁施加动荷载，施加的荷载为EL CENTRO地震波，通过对数据结果，可以得到采用互关函数法求得的动挠度的识别值和精确值之间基本一致，吻合度较高，该动挠度的测试方法可行且有效。