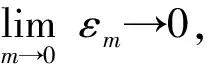非自治动力系统的D-拉回渐近紧性

韩英豪, 常译方, 崔晓旭，傅 雪

(辽宁师范大学 数学学院，辽宁 大连 116029)

拉回吸引子是随着参数变化而变化的紧集族，它能够一致地“拉回”吸引任意有界集合，并沿着系统的轨迹不变．此概念是理解非自治动力系统长时间动力行为的一个恰当而有力的工具．T. Caraballo，G．ukaszewicz和J．Real[1]提出了所谓D-拉回吸引子的概念．D-拉回吸引子的特点是不再吸引所有有界集，而是吸引所给定的随着参数而变化的一类集族．这一概念是一般拉回吸引子概念的推广和提升，一般拉回吸引子是D-拉回吸引子的特殊情况．D-拉回吸引子的概念更适用于对具体问题的分析．然而，对于这类吸引子，需要改进相应的紧性的概念．因而人们给出了拉回渐近紧的概念，并给出了相应的证明方法．G．ukaszewicz和W. Sadowski[2]利用能量方程对非自治动力系统引进了一致渐近紧的概念，并利用此概念证明了Magneto-Micropolar方程的一致吸引子的存在性．此后，T. Caraballo等[3]把此方法改变成适合于拉回渐近紧的形式．然而，这种紧性一般不适用于无界区域的抛物型和有界区域的双曲型方程．对这些情况通常采用分解方程或采用函数等几种方法．对于拉回吸引子，C．Y.Sun，Y．H．Wang等[4-5]利用收缩函数来证明了非自治动力过程的拉回渐近紧性．作者利用此方法证明了具有临界增长率的波动方程的拉回吸引子的存在性．

然而，对于D-拉回吸引子来说迄今为止证明渐近紧性的方法并不多．本文基于上述结果提出了“D-拉回渐近紧”的概念，给出了D-拉回渐近紧的等价条件，并利用收缩函数给出了D-拉回渐近紧判定定理．

1 非自治动力系统及其相关概念

首先,介绍非自治动力系统相关概念及预备知识．关于非自治动力系统的相关概念有众多不同版本，本文主要参考文献[3]和[6-7]．

设Q是一个非空集合,θ={θt}t∈是Q上的一个映射族，若满足下列性质：

(1)θ0(q)=q, ∀q∈Q;

(2)θt+τ(q)=θt(θτ(q)), ∀t,τ∈,

则称θ为Q上的一个参数动力系统．

令(X,d)为一个完备的度量空间．如果映射φ：+×Q×X→X满足如下条件：

(1)φ(0,q,x)=x, ∀(q,x)∈Q×X;

(2)φ(t+s,q,x)=φ(s,θt(q),φ(t,q,x))∀s,t∈+,(q,x)∈Q×X;

(3)映射φ(t,q,·)：X→X是连续的，∀(t,q)∈+×Q，

则称映射φ为在X上由参数空间Q上的参数动力系统θ驱动的上循环．

用D来记一类X的一些非空集族构成的集合：

D={D={Dq⊆X∶Dq≠∅,q∈Q}}．

定义1设X中给定一类有界的集族D．集族B={Bq}q∈Q称为φ的一个D-拉回吸收集，如果对任意q∈Q和X的任意D={Dq}q∈Q⊆D,存在t0=t0(q,D)>0，使得

φ(t,θ-t(q),Dθ-t(q))⊆Bq,∀t≥t0.

定义2设φ为在X上由参数空间Q上的参数动力系统θ驱动的上循环，D在X上是有界的．在X上的一族非空紧集A={Aq}q∈Q称为φ的一个D-拉回(或上循环)吸引子，如果对任意q∈Q，满足

(1)φ(t,q,Aq)=Aθt(q),∀t∈+(称φ-不变)，

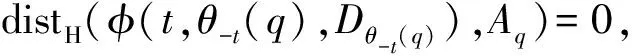
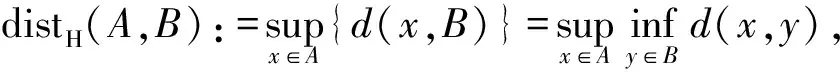
对任意ε>0，集合D⊆X的ε-开邻域定义为

Nε(D)={x∈X：d(x，D)<ε}．

2 D-拉回渐近紧性判定定理

首先,给出D-拉回渐近紧性的概念;然后,利用D-拉回渐近紧性给出D-拉回吸引子存在性的充分条件;最后，利用收缩函数给出一个上循环是D-拉回渐近紧的充分条件．

定义4设φ为在X上由参数空间Q上的参数动力系统θ驱动的上循环，D在(X，d)上是有界的．那么上循环φ称为在D={Dq}q∈Q⊆D上是拉回渐近紧的，如果对任意q∈Q，以及任意序列(xn,tn)n∈,xn∈Dθ-tn(q),tn→∞，序列φ(tn,θ-tn(q),xn)在X中存在收敛子序列．如果对任意D={Dq}q∈Q⊆D上φ是拉回渐近紧的，则称φ是D-拉回渐近紧的．

定理1设φ为在X上由参数空间Q上的参数动力系统θ驱动的上循环，D为有界，并关于邻域是封闭的．假设有界族B={Bq}q∈Q∈D是φ的D-拉回吸收集，且φ在B上是拉回渐近紧的，则φ存在唯一D-拉回吸引子A={Aq}q∈Q∈D，这个吸引子就是B关于φ的ω-拉回极限集:

证文献[8]中证明了当φ具有有界拉回吸收集，并D-拉回渐近紧的时候φ具有拉回吸引子．因而只需证明，当φ在B上拉回渐近紧的时候φ是D-拉回渐近紧的．

假设D={Dq}q∈Q⊆D,对给定的q∈Q,(xn,tn)n∈,xn∈Dθ-tn(q),tn→∞.由于B是D-拉回吸收集，B∈D，因而存在t′1>0，满足

φ(t,θ-t(q),Bθ-t(q))⊆Bq,∀t≥t′1.

又由于B是D-拉回吸收集，D={Dq}q∈Q∈D,因而存在t″1>0，有

φ(t,θ-t(q),Dθ-t(θ-t′1(q)))⊆Bθ-t′1(q),∀t≥t″1.

令B1=Bθ-t′1(q),n1=min{i:ti≥t′1+t″1,i=1,2,…},tn1=min{ti:ti≥t′1+t″1,i=1,2,…},y1=φ(tn1-t′1,θ-(tn1)(q),xn1).则y1∈B1,φ(t′1,θ-t′1(q),y1)∈Bq.

利用归纳法，假设Bi,ni,t′i,t″i以及yi已经有定义．如同上述证明，存在t′i+1>t′i，使得

φ(t,θ-t(θ-t′i(q)),Bθ-t(θ-t′i(q)))⊆Bi=Bθ-t′i(q),∀t≥t′i+1-t′i，

以及存在t″i+1>0，使得

φ(t,θ-t(θ-t′i+1(q)),Dθ-t(θ-t′i+1(q)))⊆Bθ-t′i+1(q),∀t≥t″i+1.

令Bi+1=Bθ-t′i+1(q),ni+1=min{j:tj≥t′i+1+t″i+1,j=ni+1,ni+2,…},tni+1=min{tj:tj≥t′i+1+t″i+1,j≥ni+1},以及yi+1=φ(tni+1-t′i+1,θ-tni+1(q),xni+1).则

yi∈Bi=Bθ-t′i(q),φ(t′i,θ-t′i(q),yi)=φ(tni,θ-tni(q),xni)∈Bq,i=1,2,…

由于φ在B上为拉回渐近紧的，因而存在子序列{yik}k∈⊆{yi}i∈,使得φ(t′ik,θ-t′ik,yik)∈Bq收敛．因而，序列{xnik}k∈⊆{xi}i∈,得使φ(tnik，θ-tnik(q),xnik)∈Bq收敛．

下面给出验证上循环φ是D-拉回渐近紧的一种方法，为此需要给出以下概念(参见文献[4])．

定义5设X是一个Banach空间，φ为在X上由参数空间Q上的参数动力系统θ驱动的上循环，B⊆X为一个有界集合，在B×B上的一个函数Ψ(·，·)称为收缩的，如果对任意序列{xn}n∈⊂B，存在子序列{xnk}k∈⊂{xn}n∈，使得

定理2设X是一个Banach空间，φ为在X上由参数空间Q上的参数动力系统θ驱动的上循环，D为一些有界非空集族构成的集合．B={Bq}q∈Q∈D为φ的一个D-拉回吸收集．假设对任意ε>0,q∈Q,t0>0，存在t=t(ε，B,q,t0)≥t0和一个定义在Bθ-t(q)×Bθ-t(q)上的收缩函数Ψt,q,B(·，·)，使得

‖φ(t,θ-t(q),x)-φ(t,θ-t(q),y)‖X≤ε+Ψt,q,B(x,y) ∀x,y∈Bθ-t(q),

其中,Ψt,q,B依赖于t,q,B．那么φ在X中是D-拉回渐近紧的．

证设给定任意q∈Q,任意序列{tn}n∈,tn→+∞和一个序列xn∈Bθ-tn(q)，将证明序列{φ(tn,θ-tn(q),xn)}n∈有一个收敛子列．

首先，由于B={Bq}q∈Q为φ的一个D-拉回吸收集，B∈D，因而存在t′0>0，当t≥t′0时,

φ(t,θ-t(q),Bθ-t(q))⊆Bq.

(1)

其次，给定一个序列{εi:εi>0,i∈},满足：由假设，对εi，存在t″i=t″i(εi,B,t′0)≥t′0和一个定义在Bθ-t″i(q)×Bθ-t″i(q)上的收缩函数Ψt″i,q(·,·),使得

(2)

φ(t-t″i,θ-(t-t″i)(θ-t″i(q)),Bθ-(t-t″i)(θ-t″i(q)))⊆Bθ-t″i(q).

因而，当tn≥t′i时，

φ(tn-t″i,θ-(tn-t″i)(θ-t″i(q)),xn)∈Bθ-t″i(q).

对给定的i，对任意满足tn≥t′i的n∈，记

yn=φ(tn-t″i,θ-(tn-t″i)(θ-t″i(q)),xn)∈Bθ-t″i(q).

则有yn∈Bθ-t″i(q),由式(1),有φ(tn,θ-tn(q),xn)=φ(t″i,θ-t″i(q),yn)∈Bq,因而根据式(2)有

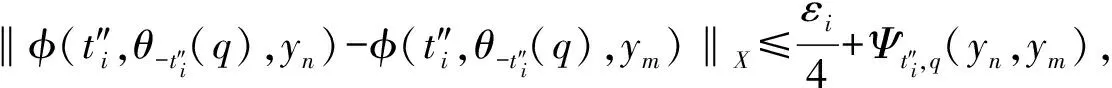
(3)

对任意n，m∈i：={n∈：tn≥t′i}．由于Ψt″1,q是在Bθ-t″1(q)上的收缩函数，因而序列,yn∈Bθ-t″1(q)}存在一个子列以及N′1>0，使得

从而,对任意k1,k2≥N′1,存在k(1,2)>0,使得tnk(1,2)≥t′1，而且

(4)

结合式(3)与式(4)，对任意k1,k2≥N′1,有