一类完全非代数连接纽结与链环的构造
王树新, 王鹤潼, 李思宇, 王冬雪
(辽宁师范大学 数学学院,辽宁 大连 116029)
1970年,J.H.Conway[1]从链环可进行缠绕分解的角度出发,指出任何链环的投影图都可以分解成代数缠绕的集合,并给出了代数链环的定义,同时介绍了链环投影图与其基本多面体之间的关系;2005年,C.L.McCabe[2]结合树图的有关知识,给出了将代数链环的代数投影图转化为标准形式的代数投影图的具体方法,并给出了MAP(最小代数表示)链环的棍棒指标估计,同时指出代数链环的非代数投影图至少由6个代数缠绕构成;2005年,E.Insko[3]给出了任意非代数纽结和链环与完全非代数连接基本多面体之间的关系,同时给出了非代数纽结和链环新的棍棒指标估计. 本文从上述角度出发,构造性地证明了对于任意的自然数n(n≥6,n≠7)均存在完全非代数连接基本多面体,进而证明了完全非代数连接纽结与链环的广泛存在性.
1 预备知识
定义1.1[4]设(B,t1∪t2)是一偶对,其中,B是一个三维实心球体,t1,t2是B中的2条互不相交的弧段,若ti∩∂B=∂ti(i=1,2),则称偶对(B,t1∪t2)是一个2-缠绕.
注1.1本文所指的缠绕均为2-缠绕.
定义1.2从0-缠绕出发,做n次正(负)水平扭转形成的缠绕称为水平整数缠绕,记为水平+n(-n)-缠绕;从∞-缠绕出发,做n次正(负)竖直扭转形成的缠绕称为竖直整数缠绕,记为竖直+n(-n)-缠绕;水平整数缠绕和竖直整数缠绕统称为整数缠绕.
定义1.3设T1,T2是两个缠绕,若缠绕T1,T2间至少通过2段弧相连,则称缠绕T1和T2以代数方式连接.
定义1.4设T是一个由n个整数缠绕Ti(1≤i≤n,n∈+)彼此连接构成的缠绕,若任意2个缠绕Ti,Tj间均通过代数方式连接,其中,i≠j且1≤i,j≤n,则称缠绕T为一个代数缠绕.
定义1.5设L是一链环,DL是L的任意投影图,将DL中的每个整数缠绕Ti用1个顶点vi(i≥1,i∈+)来代替,此时DL对应得到1个平面四岔图,记为GDL.若GDL中至少存在2顶点间由2段弧相连,则可对GDL进行如图1所示的局部变形,将vi,vj2个顶点缩成1个顶点vi,j(i,j≥1,i,j∈+),对GDL中所有满足上述条件的局部进行收缩变形,直到对应的平面四岔图不能再进行如图1所示的收缩变形为止,记得到的平面四岔图为BGDL,则称BGDL为DL对应的基本多面体. 若BGDL中的任意顶点均与其他4个不同的顶点相连,则称BGDL中的点以完全非代数方式连接,此时称BGDL为完全非代数连接基本多面体,进一步地称链环L为完全非代数连接链环.
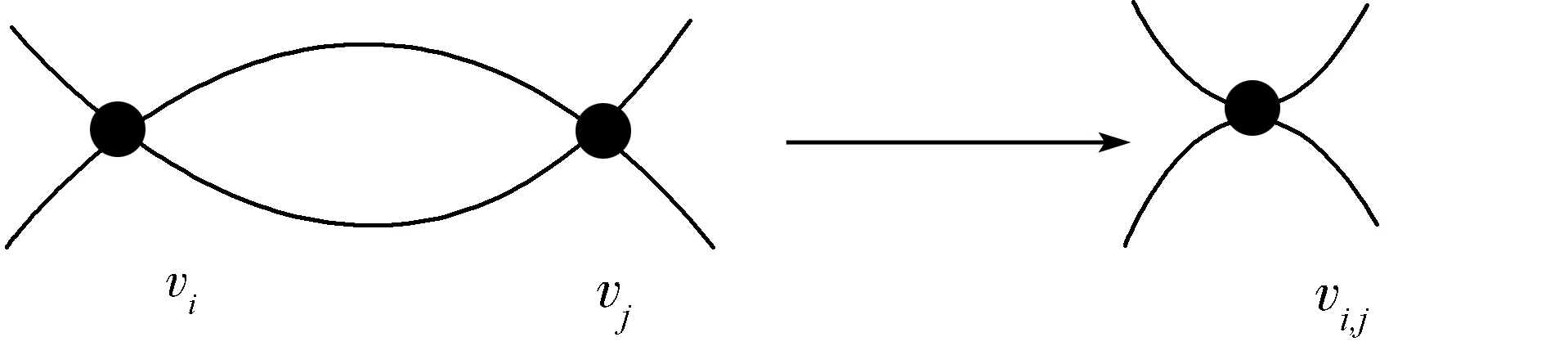
图1 平面四岔图GDL的局部收缩变形Fig.1 Local shrinkage deformation of 4-valent planar graph GDL
命题1.1设L是一链环,DL是L的任意投影图,BGDL为DL对应的基本多面体且BGDL具有7个顶点,则BGDL一定不是完全非代数连接基本多面体.
注1.2命题1.1通过组合构造的方法即可证明.
本文中未给出的概念和术语都是标准的,参见文献[5-8].
2 主要结果
定理2.1对∀n≥6(n≠7,n∈+),一定存在一个具有n个顶点的完全非代数连接平面四岔图.
证设v1,v2,…,vn(n∈+)是n个互不相同的顶点,下面分情况讨论n的取值.
(1)n为合数.
由n是合数可知n可表示为j×i(i,j∈+),易知i≥2,j≥2,且i,j不同时为2. 下面给出具有n个顶点的完全非代数连接平面四岔图的构造方法,具体操作如下:
首先,选取一个由j个顶点(j≥3)构成的j边形为中心图形,在j边形的各边外分别增加1个顶点,如图2(1)所示,并将新增加的顶点与原顶点按如图2(2)所示的方式连接,此时可得到一个具有2j个顶点的图形,记为P2j,由完全非代数连接的定义,可知P2j是一个完全非代数连接平面四岔图.
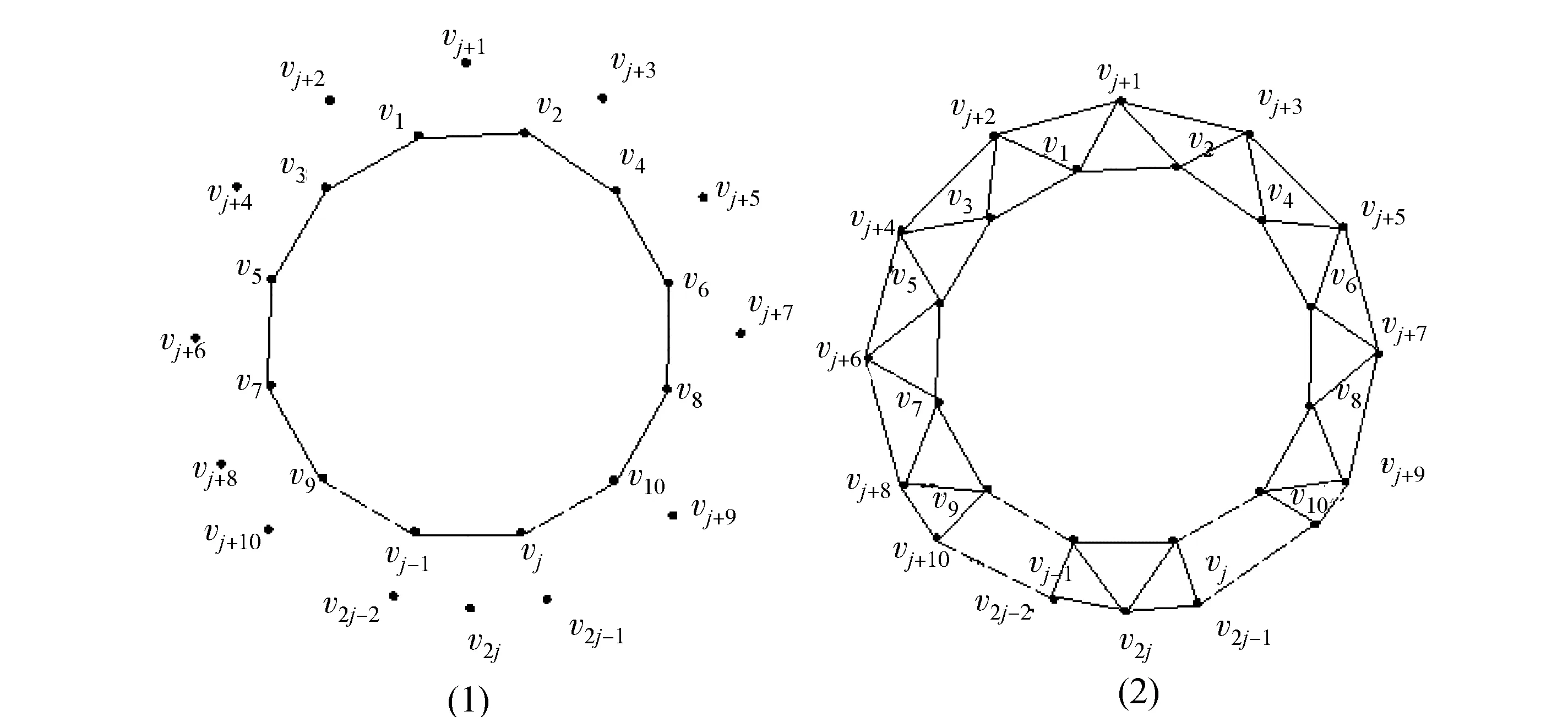
图2 具有2j个顶点的完全非代数连接平面四岔图P2j的表示Fig.2 The representation of completely non-algebraic connected 4-valent planar graph P2j which has 2j vertices
接下来在P2j最外面的j段弧上分别增加顶点v2j+1,v2j+2,…,v3j,并将每个新增加的顶点分别同与它相邻的新增加的2个顶点相连,此时得到一个具有3j个顶点的图形,记为P3j,如图3所示,由完全非代数连接的定义可知P3j是一个完全非代数连接平面四岔图,继续进行从P2j到P3j相同的构造过程,每次增加j个顶点,增加i-2次,即可得到由n个顶点构成的完全非代数连接平面四岔图Pn.
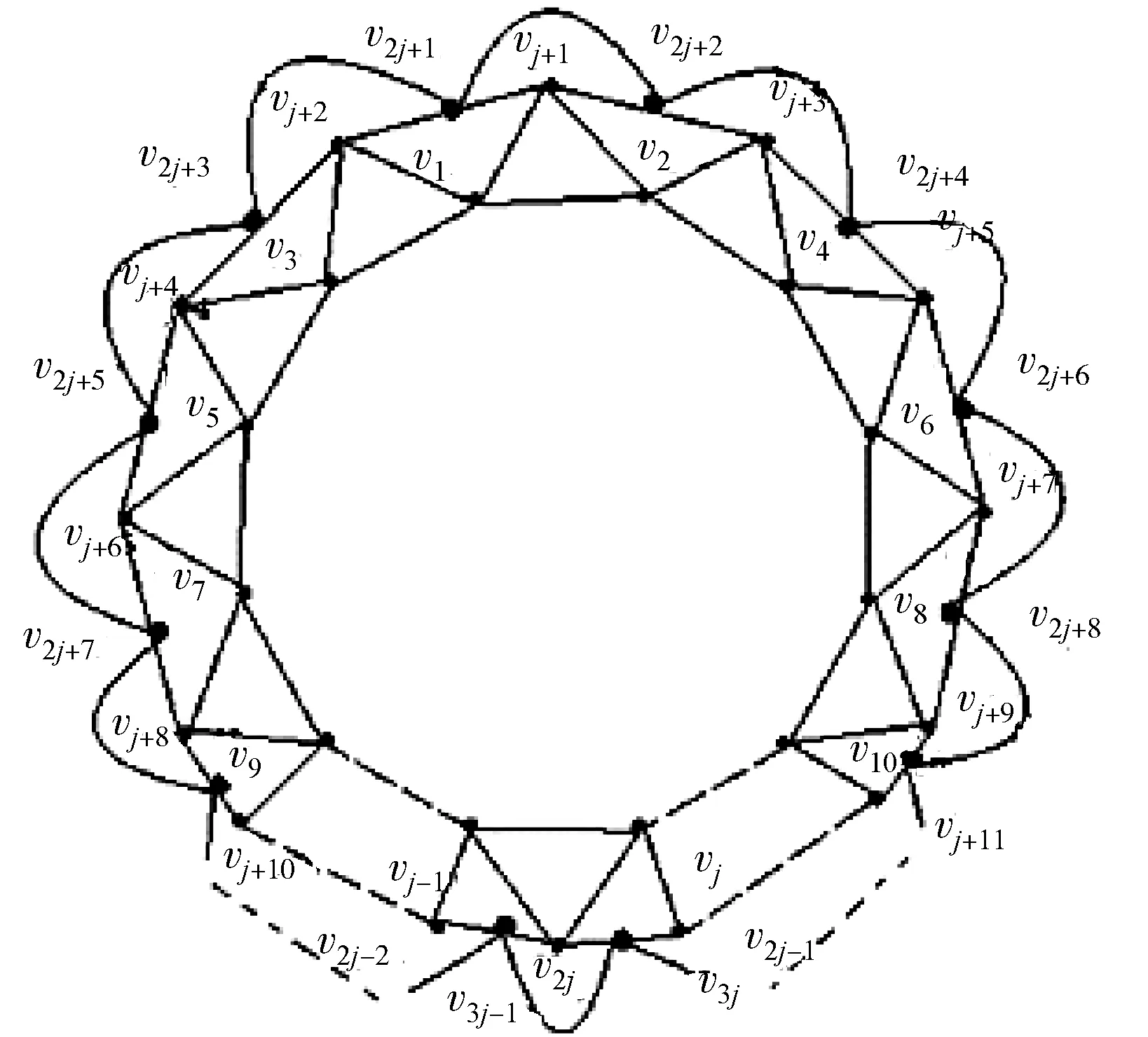
图3 具有3j个顶点的完全非代数连接平面四岔图P3j的表示Fig.3 The representation of completely non-algebraic connected 4-valent planar P3j which has 3j vertices
综上所述,对任意的n≥6且n为合数时,定理均成立.
(2)n为质数.
由命题1.1可知n≠7,显然此时n可由11+4i或13+4i(i≥0,i∈+)表示.下面分情况说明.
①n=11+4i
首先,考虑i=0,即n=11. 此时任取11个顶点v1,v2,…,v11. 不失一般性,不妨设从v1出发的4段弧分别与v2,v4,v5,v7相连,从v13出发的4段弧分别与v8,v10,v5,v7相连,对于未完成连接的顶点vj(2≤j≤10)进行如图4所示的连接,记得到的图形为P11,由完全非代数连接的定义,可知P11是一个完全非代数连接平面四岔图.

图4 具有11个顶点的完全非代数连接平面四岔图P11的表示Fig.4 The representation of completely non-algebraic connected 4-valent planar graph P11 which has eleven vertices
接下来考虑n=11+4i(i≥1)的情形. 此时,从P11出发,在P11最外侧的4段弧上分别增加一个顶点v12,v13,v14,v15,并将新增加的顶点以如图5所示的方式连接,记得到的图形为P15.
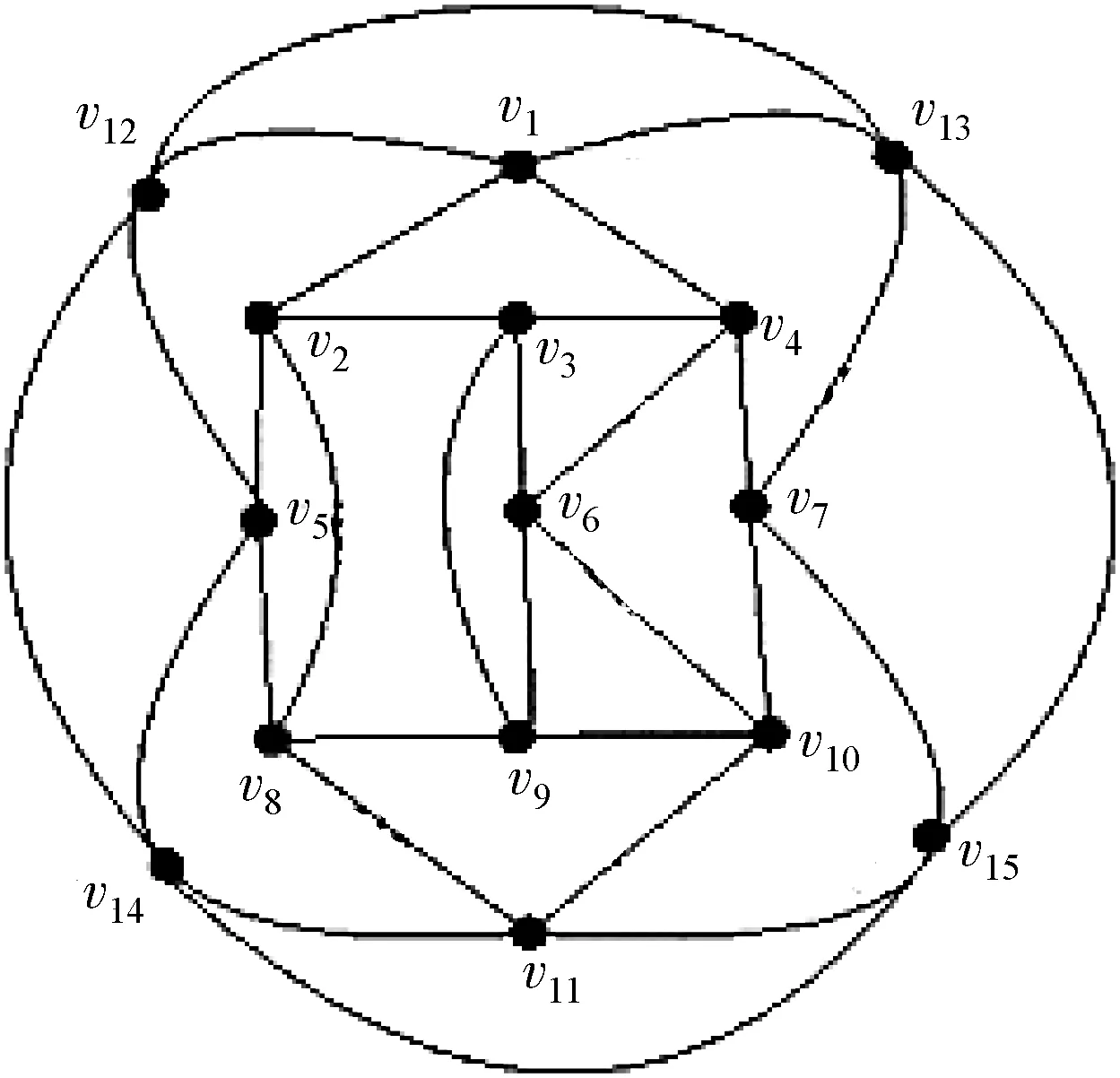
图5 具有15个顶点的完全非代数连接平面四岔图P15的表示Fig.5 The representation of completely non-algebraic connected 4-valent planar graph P15 which has fifteen vertices
重复上述操作,每次均在P11+4k(1≤k≤i-1)最外侧的4段弧上分别增加一个顶点,最终可得到由11+4i个顶点构成的完全非代数连接平面四岔图Pn.
②n=13+4i
首先,考虑i=0,即n=13. 此时任取13个顶点v1,v2,…,v13. 不失一般性,不妨设从v1出发的4段弧分别与v2,v4,v5,v9相连,从v13出发的4段弧分别与v10,v12,v5,v9相连,对于未完成连接的顶点vj(2≤j≤12)进行如图6所示的连接,记得到的图形为P13,由完全非代数连接的定义,可知P13是一个完全非代数连接平面四岔图.
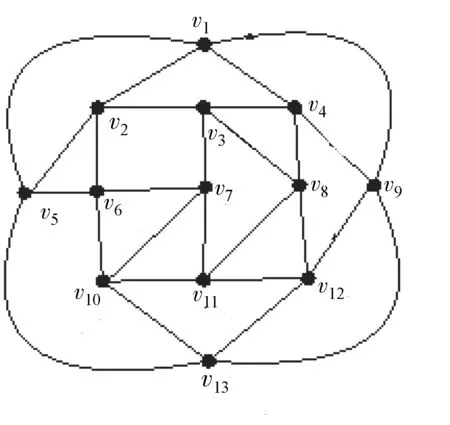
图6 具有13个顶点的完全非代数连接平面四岔图P13的表示Fig.6 The representation of completely non-algebraic connected 4-valent planar graph P13 which has thirteen vertices
接下来考虑n=13+4i(i≥1)的情形. 此时,从P13出发,在P13最外侧的4段弧上分别增加一个顶点v14,v15,v16,v17,并将新增加的顶点以如图7所示的方式连接,记得到的图形为P17.
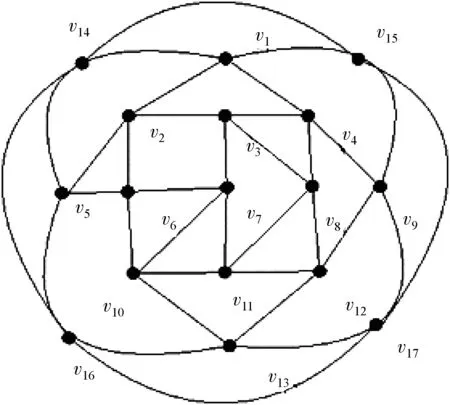
图7 具有17个顶点的完全非代数连接平面四岔图P17的表示Fig.7 The representation of completely non-algebraic connected 4-valent planar graph P17 which has seventeen vertices
重复上述操作,每次均在P13+4k(1≤k≤i-1)最外侧的4段弧上分别增加一个顶点,最终可得到由13+4i个顶点构成的完全非代数连接平面四岔图Pn.
综上,定理得证.
推论2.1∀n≥6(n≠7,n∈+)均存在任意多个完全非代数连接纽结与链环.
证由定理2.1可知,对于∀n≥6(n≠7,n∈+)均存在由n个顶点构成的完全非代数连接基本多面体BGDL,将BGDL中的每一个顶点用任意缠绕代替,即可得到一个完全非代数连接纽结与链环,由缠绕的任意性可知,∀n≥6,n≠7,均存在任意多个完全非代数连接纽结与链环.

