风险视角下公共工程多项目决策评价研究

杨 苏，林浩东

(1.安徽建筑大学 经济与管理学院，合肥 230601；2.安徽省建筑经济与房地产管理中心，合肥 230601)

公共工程项目是指由政府投资的各类旨在提供公共服务和实现各种社会目标，并且不完全由市场资源配置的项目，包括道路、桥梁、电力、通信等与人民生活息息相关的基础设施建设项目[1]。据统计，超过九成的公共工程项目是在多项目背景下完成的，但政府在面对多项目抉择时往往具有随意性，缺乏科学的比较，导致了一些项目无法保质保量的完成，造成了不好的社会影响。因而在面对这类项目时，如何抉择出更适合的项目进行优先投资显得尤为重要。

国内有关项目风险评价方法包括定性分析和定量研究。随着信息网络技术的不断发展，数据处理、采集等方面的能力也得到了提升，更多的评价方法得到应用，包括IFS方法、物元模型以及多模型相结合的评价方法[2-3]，评价的方向和结论也越来越有意义。马力[4]采用COWA 算子和非线性云物元模型相结合，较好地对政府公共工程项目投资风险进行测度与预警。王帅[5]运用系统动力学对风险因素进行了识别，再分析其权重，评价体系更加系统全面。何亚伯[6]对项目建设中的风险因素和参与者风险分担的大小进行了比较，使得结果更加客观。张云宁[7]将BP神经网络引入了项目风险评价，提高了项目管理能力。段世霞[8]对公共工程项目分别从经济、社会、生态三个方面进行了绩效协同评价，更好的体现了公共工程项目的特点。此外，还有包括粗集理论，D-S理论等方法。

然而在现有关于公共工程项目风险评价研究缺乏项目开始之前多项目择优问题的思考，单纯地从权重角度分析风险因素，往往具有更多的主观性。文章通过对公共工程项目进行调查，结合公共工程项目的特点及前人研究基础，更合理地从项目开始之前对项目进行择优建设，提出了更加科学有效的公共工程项目风险评价指标体系。通过专家打分法对样本评价指标进行0-1打分，为降低极端打分结果对评价结论的影响，采用了熵权法进行权重计算。再对结果进行灰色关联分析，利用理想解排序法计算被评价项目与理想项目之间的贴近度，对评价项目进行排序，最后通过实例证明该方法的有效性，进而为决策者提供决策参考。

1 公共工程项目风险评价指标体系构建

公共工程项目不同于其他类建设项目，其项目特点导致其风险因素相互之间关系错综复杂，具有特殊性。一是政府参与，二是建设规模往往大并且复杂，三是项目建设更多是为社会服务[9]。根据这些特点在大量阅读相关文献和有关案例的基础上，参照胡芳[10]的方法，将公共工程项目风险整体从外部风险、内部风险以及自身风险进行考虑。并结合钟登华[11]、丛旭辉[12]等人对公共工程项目中评价指标的分类，对公共工程项目风险因素进行了提炼，将公共工程项目风险指标分为外部风险、内部风险和自身风险3个一级指标，以环境风险、经济风险、政治风险、建设风险、管理风险、运营风险、项目自身性质风险、自身资源风险8个二级指标以及多个三级指标，构建了公共工程项目风险评价指标体系见表1。

2 基于TOPSIS法和灰色关联度的综合评价方法

传统的熵权法、灰色关联度以及Topsis方法都有着各自的优缺点，单独使用时不能较为全面的对项目进行评价。本文在综合三种方法特点的基础上提出了熵权法-灰色关联度-Topsis综合评价模型。运用熵权法来计算被评价项目各指标权重，然后通过计算各评价项目与最理想项目和最不理想项目的模糊关联性来确定各评价项目的综合重要程度。

2.1 熵权法确定风险指标权重

2.1.1构建规范化指标矩阵

假设现有m个可投资的公共工程项目，每个公共工程项目有n个评价指标，指标值为rij(i=1,2,…,m;j=1,2,…,n)，则指标矩阵为:Z=(zij)mn。

(1)

由于评价指标之间的各种差别，为避免对结果产生影响，从而需要按照公式(2)对(1)进行规范化处理，得到无量纲化指标矩阵X=(xij)m×n。

(2)

2.1.2确定权重

这里，利用熵权法确定各评价指标的权重。

(3)

(4)

(5)

式中：wj表示第j项指标的熵权；uij,vi则为计算过程中的中间变量，求得指标权重列向量为：

W=(w1,w2,…,wn)T

(6)

其中:wi指第i项指标权重。

2.1.3加权标准化

由公式(2)(6)所得结果可求得加权标准化矩阵R

R=(rij)m×n=(wixij)m×n

(7)

式中:rij表示第i个样本第j个指标的值。

表1 公共工程项目风险评价指标体系

2.2 灰色关联分析确定风险指标间距离与灰色关联度

2.2.1计算各风险指标间的距离

由加权标准化矩阵R求得正理想解R+以及负理想解R-。

(8)

(9)

式中：j+和j-分别为正向指标和负向指标。

(10)

(11)

2.2.2确定灰色关联度

根据前述计算各指标与正理想解和负理想解的灰色关联度，基于加权标准化矩阵，分别计算样本指标与正理想解和负理想解关于第j个指标的灰色关联系数[13]。

(12)

(13)

(14)

(15)

2.3 根据Topsis方法确定相对接近度

首先，对所得结果进行无量纲化处理，得：

(16)

根据上述结果可求：

(17)

(18)

(19)

依据计算得到δi值对指标的重要性进行排序，δi越大，则待评价指标越优；反之越差。

3 实例分析

3.1 构造加权标准化矩阵

选取安徽省8个市的公共工程项目作为实证研究的对象，项目1为XX市的桥梁建设项目，项目2为XX市的道路建设项目，项目3为XX市的水利建设项目，项目4为XX市的电力建设项目，项目5为XX市通信建设项目，项目6为XX市的教育建设项目，项目7为XX市医疗建设项目，项目8为XX市体育馆项目。根据相关资料通过专家打分法的方式分别对自然环境风险、政治风险、经济风险、建设风险、管理风险、运营风险、项目本身性质风险、自身资源风险8个方面对8个公共工程项目分别进行打分，结果见表2。

表2 项目风险打分结果

使用熵权法计算各指标的权重，其结果见表3。

表3 指标权重

得到指标权重过后，根据公式(7)可求得加权标准化矩阵R：

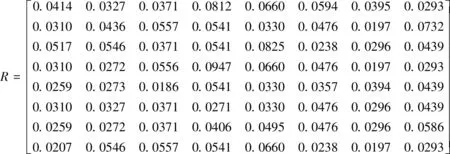
3.2 计算欧氏距离和灰色关联度

在所构建的风险管理体系中，由于A1～A8均属于成长性指标，所以可求得正理想解R+以及负理想解R-。

R+=(0.0207,0.00273,0.0186,0.0271,0.0330,

0.0238,0.0197,0.0293)

R-=(0.0517,0.0546,0.0557,0.0947,0.0825,

0.0595,0.0395,0.0732)

由得到的正负理想解结合前面的公式可求样本与正负理想解的欧氏距离以及灰色关联度，见表4。

表4 欧氏距离和灰色关联度

3.3 计算相对贴近度

对表4所得到的与正负理想解的欧氏距离和灰色关联度分别进行无量纲化处理，得出样本与正负理想解的接近程度，结果见表5。取c1=c2=0.5，最后依据公式(19)算出相对贴近度，结果见表6，最后实现对样本的排序。

表5 样本与正负理想解的接近程度

表6 相对贴近度

从表5结果看出，8个被评价项目得分从高到低依次是4,1,3,8,2,7,5,6。本文将灰色关联度改进的TOPSIS法运用到了公共工程项目中，可知评价的结果越小越优，样本越贴近正理想解说明其可能面临的风险就越大，所以由表5可知，项目6的得分最低，说明项目6风险最小，而项目4得分最高，说明项目4面临的风险最大。

4 结论

本文分析了公共工程项目的特殊性，对公共工程项目的风险因素进行了探讨。建立了基于熵权法-灰色关联度-TOPSIS方法的公共工程项目风险综合评价模型，对风险指标进行评价。通过实例证明其对公共工程项目风险评价的意义，得出了一些结论和建议。

第一，使用熵权法根据数据的信息量确定指标权重，结合TOPSIS与灰色关联法对公共工程项目的风险进行综合评价。熵权法在有可靠的数据基础上，相较于层次分析法等数据处理方法带来的结果更加精确。同时评价结果也会根据实际情况发生调整，更加具有动态性，更具有实施性。

第二，建立公共工程项目风险评价灰色理想值逼近模型进行评价，相较于现有的风险评价方法，它既可以从整体上对项目进行评价，还可以从内部进行评价，分析内部因素的变化趋势以及不同于理想项目的地方，较之传统方法更加具有全面性，对管理者进行多项目决策具有参考价值。

第三，通过对8个案例的实证分析表明，8个建设项目的相对贴近度从大到小顺序为项目4>1>3>8>2>7>5>6；鉴于改进的TOPSIS方法的特点，在应用到公共工程项目中时，其风险评价结果越小越好。因此，最优为项目6，最差为项目4。此方法更贴近实际情况，优选方案案更加可靠。但与此同时，为避免人为经验因素影响，对风险因素的定量分析也显得愈加重要，因而模型也要根据实际情况进行修正。如何联系实际情况进行数据分析，使项目决策更加因地制宜是值得思考的问题。