危化品运输车载监测系统判决方法研究
赵 正,王 磊,赵志国,王金升,朱建辉
(1.中国交通通信信息中心,北京 100000;2.淮阴工学院 交通工程学院,江苏 淮安 223001)
目前,80%的国内危险化学品需要通过高速公路运输,每年通过公路运输的危险货物总量达 3 亿吨。随着经济快速发展,危化品货物运输量也呈上升趋势。据相关实验可知,运输途中的危险化学品,不可控因素众多,就相当于移动着的隐形炸弹,一旦出现意外,影响甚大,将会对周边居民的生命和财产造成极大的危害。因此,对危化品运输车监测以及预警研究具有很好的社会效益和经济效益[1]。
以危险品在运输途中的各种状态为目标,有针对性地选择多种传感器来实现数据的采集,在整体结构设计的基础上构建系统功能,以信号处理技术为基础,将多传感器信号进行处理和融合[2],以GPS 车辆定位方法,以 4G 作为传输方式,来完成危险化学品运输过程中的探测、跟踪与监测,并通过车载终端和远程服务端两者相结合进行实时报警,同时根据危化品行业的相关应急处理机制,减少和避免事故的二次危害,提高我国危险化学品运输的安全性与可靠性[3]。
西南交通大学的杨一帆利用 DSP 设计了一种新型的气体监测器[4],用于实时监测罐体在运动过程中的气体浓度变化。西南交通大学康团结基于 DBSCAN 聚类和 ZigBee 技术,采集了车辆的温湿度,其部分传感器使用 MEMS 微传感器。中国地质大学的王晓欢以物联网为载体,通过 MEMS 传感器采集位置、速度和温度等数据信息,最后通过物联网上传后台,并实现车辆轨迹绘制功能[5]。但在部分传感器失效或者异常时,系统算法处理不是很精准,存在误警的状况。针对油气管道泄漏监测系统中存在较高的误报率,冯健等人采用基于加权值分配的 D-S 合成规则对数据信息进行融合,提高监测系统的精度。但在构造基本概率分配函数时,所采用的方法不适合具体的应用场景,从而导致构造结果中出现证据有冲突。目前,危化品运输系统缺少适用的安全评价模型,数据融合尚未建立完整,成熟的理论和方法,但许多领域的研究人员根据其应用提出了一些有效的融合方法。通过对比,本文确定使用 D-S 论据理论,重点搭建运输安全评价模型,并介绍评价模型中引用的算法理论,同时举例验证模型的可行性。
1 构建运输安全评价模型
在危化品运输过程中,运输状态的一个变化量往往会导致多个信息也伴随着变化。例如:车辆受到碰撞后,加速度会出现急剧异常的波动,伴随而来的是罐内液位引起明显波动变化和罐内压力的瞬间异常变化;当发生车辆侧翻事故时,罐车横向角会发生变化,罐内的危化品液位也会发生由倾斜带来的变化;如果出现液体泄漏情况,不仅气体传感器会检测到泄漏浓度信息变化之外,罐内的压力、液位也会在同一时刻发生变化。
运输系统中,故障可以从三方面找,第一是车辆原因,超速、侧翻、追尾等;第二危化品原因,泄露、超载等;第三是环境原因,环境温度过高、湿度太大等,3种原因都会引起运输事故,针对这些[6-7],本文建立了运输安全评价模型。通过多传感器数据采集,融合处理,为事故提供评价,在事故即将发生时,为驾驶员和公司提供可靠的报警信息。
1.1 构造基本概率分配函数
假设存在一组证据{x1,x2,x3,…,xm},xi(i⊆m)为某一传感器输出值,待识别的目标模式为{u1,u2,u3,…,un},uj(j⊆n)为某一目标模式。对于任一uj,需要确定此模式下的各个传感器输出的典型值{x1j,x2j,x3j,…,xmj} 称为典型样本[8]。对于任一xi,与目标模式uj典型样本中此条证据对应的值xij之间的汉明距离为:
与所有目标模式的汉明距离之和为:
Hij=|xi-xij|
(1)
与所有目标模式的汉明距离之和为:
(2)
定义任何一条证据xi对目标模式uj的信度函数分配为:
(3)
其中:j=1,2,…,n。可以验证,以上构造方法满足条件信度函数分配的定义。根据式1,当证据xi距离目标模式典型样本xij的距离越近,说明两者越像,最终融合结果也越近,这时的信度函数分配值也越大。
典型样本获取信度函数在很多行业已经有了使用,只要确定目标模式的典型样本,就能得到该证据的信度函数。可以有效地构造出证据理论的基本概率值,在危化品行业中,专家经验与实验数据可以容易获得典型样本,本文选择的就是该方法来确定基本概率值。
1.2 数据融合理论
证据理论的核心内容就是合成规则,其中包含 “证据” 和 “组合”,不确定、不知道的信息数据,就是 D-S 算法需要处理的 “证据”“组合”,将这些不同类型的数据进行整合,使用一定的组合规则,来得到一个全面的结论。多传感器系统中,D-S 证据理论是常用的算法之一。证据理论处理数据问题时,通过可信度赋值给传感器信息,保留信息时,也简化未知概率分布。D-S 证据理论的最大优势在于先验数据比概率理论更容易获得,这些优点使证据理论的应用领域更为广泛,在信息融合、多属性决策分析、人工智能等方面都有很好的应用。
证据理论借助合并多重证据获取决策结论,在贝叶斯推理基础上的推广,是一种信息推理决策理论,两者根本的分歧是是否利用先验信息。当概率很弱的推理系统中,信息的“不准确”“不确定”,导致贝叶斯理论的判别有误差,这也就是为什么在推理系统中,D-S 应用普遍的原因。D-S 的似然函数、信任函数就是用来解决系统的不确定性和不知道的差异。D-S 证据理论中不确定性信息的描述采用 “区间估计”,而非 “点估计”,为证据收集更有灵活性。在处理证据理论问题时,搭建识别框架,构造命题的基本概率指派函数,以及合成规则都是重要的步骤[9],只有符合系统,才能作出正确的决策[10]。
定义1:设D为辨别框架,由一完备且互不相容的命题集合组成幂集2D,在其上定义基本信任指派函数(BPA,Basic Probability Assignment):m(A)⊆[0,1],A代表辨别框架中任一子集,m(A)表示证据支持命题A发生的程度,m(A)满足如下条件[11]:
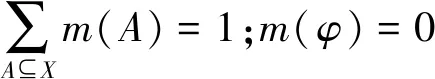
(4)
m(A)称为A的基本数。
定义2:信任函数(Belief Function)Bel(A)表示所有真属于A的假设,即B,命题A的总信任度,其定义为:

由定义可知:
m(φ)=0;m(D)=0
(5)
似然函数(Plausibility Function)表示决策者对不反对命题A的程度,所有与A相交不为空的命题B的mass值的和,其定义为:
pl(A)=1-Bel(A-)
通过信度函数和似然函数,D-S证据理论就明确表示了“不确定”和“不知道”等概念[12],详见如图1所示:

图1 D-S不确定区间
定义3:若A⊆D且A≠0,称A为m的一个焦元(Focal Element)。
Dempster合成法则(Dempster’S Rule of Combination)是反映证据的联合作用的一个法则,可概括如下:
假设判别框架上D的两个证据m1,m2,并分别含有焦元C1…Cn和B1…Bn。Dempster合成法则运算为正交和m=m1⊕m2。m为组合产生的新的证据体。
m(A)=m1(B)⊕m2(C)
A≠Φ
(7)

(8)
K称为归一化系数,表示两个证据之间的冲突程度,k∈[0,1]。当k=1或者无穷接近1时,表示证据之间完全矛盾,融合会产生“Zadeh悖论”,得出的结果有巨大偏差,故不能应用Dempster 组合规则,如果k=0,则不用归一化。
对于多个信度函数的合成。m1,m2,…,mn为2D上的n个BPA,它们的正交和m=m1⊕m2⊕…⊕mn为
m(A)=
(9)
其中
(10)
2 基于D-S证据理论的数据融合模型
利用证据理论融合,必先确定证据理论的识别框架[13],根据监测需求,建立识别模型,危险化学品输车的4类状态:U1是车体故障,U2是危化品故障,U3是环境故障,U4是正常模式,识别框架U为U={U1,U2,U3,U4},选取车辆姿态(倾角)、运行速度、加速度、环境温度以及泄露浓度这五个参数为监测指标[12],结合专家知识与智能算法,采用基于典型样本的信度函数获取方法,然后通过D-S规则融合获得最终结果。决策的结构模型如图2所示。

图2 基于 D-S 证据理论的预警模型
3 实验与分析
为了检验警报是否能在测量值超过阈值时触发,而采用较低的阈值进行测量。选取车辆姿态(倾角)、运行速度、加速度、环境温度以及泄露浓度这5个参数为监测指标。
通过实验室的系统平台随机测量得到数据,见表1。
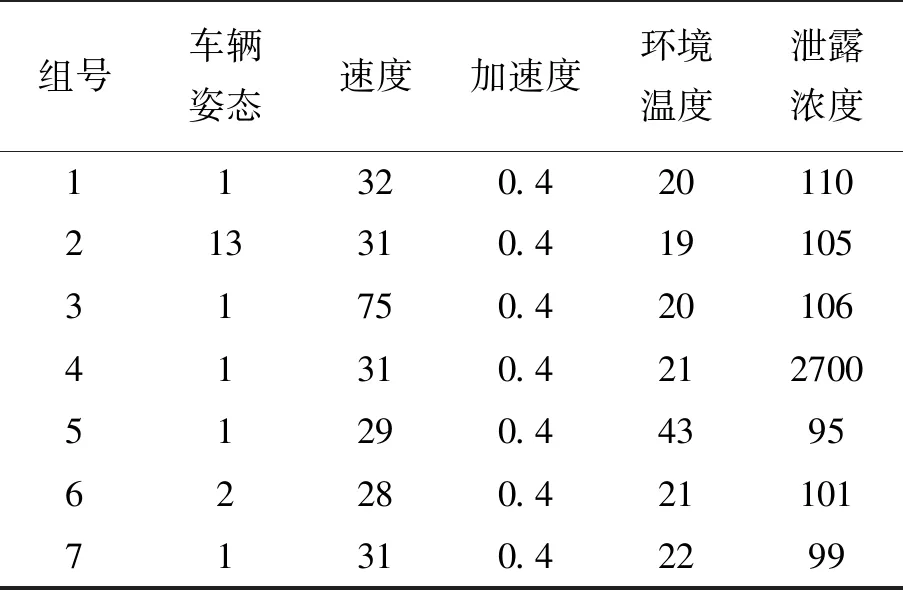
表1 测量数据
建立模型,危险化学品运输车的4类状态:U1是车体报警,U2是危化品报警,U3是环境报警,U4是正常,根据实验数据,结合专家经验,确定4组数据作为典型样本,见表2。
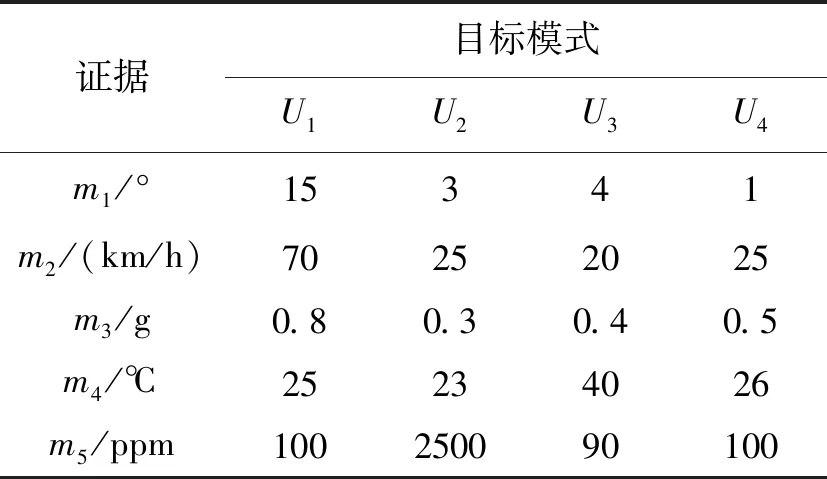
表2 目标模型的典型样本
设判定规则的阈值ε为0.50。
实例代入,辨识框架U={U1,U2,U3,U4},根
据公式3,计算证据源,见表3。

表3 融合后的结果
根据公式(11),计算K值:K= 0.52<1
(11)
根据公式(12),融合后的值为:0.0086。
(12)
同理计算出m1与m2的U2,U3,U4融合结果,重复上面步骤计算出结果,见表4。
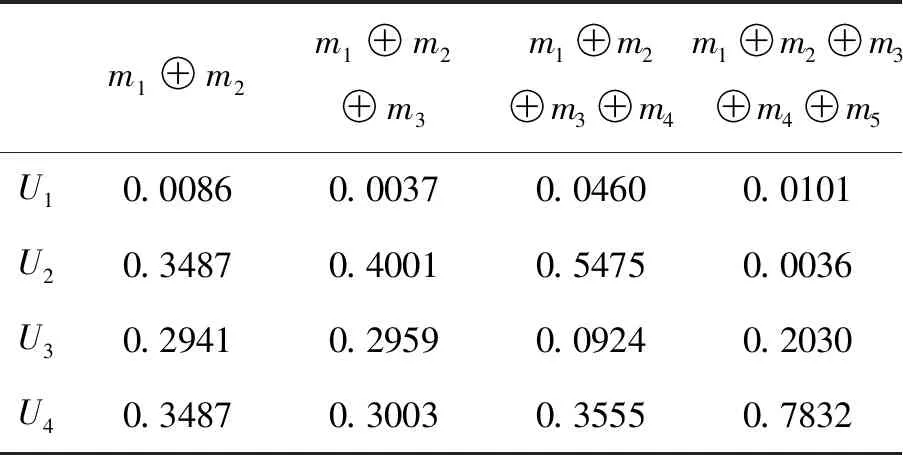
表4 D-S数据融合
通过MATLAB数据仿真,数据融合结果见图3。
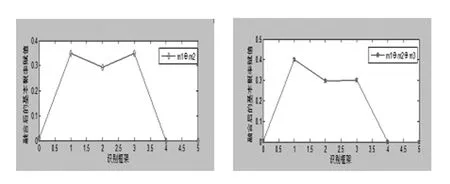
(a) 两个证据体 (b) 三个证据体
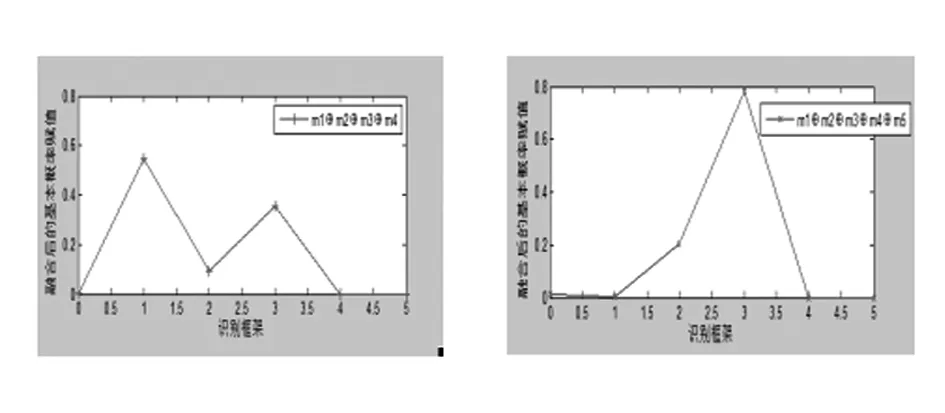
(c) 四个证据体 (d) 五个证据体
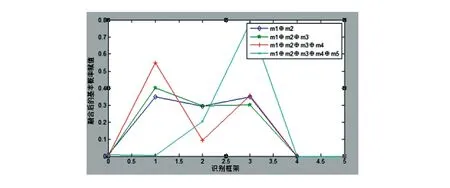
图3 D-S各数据融合结果
根据环境,选择判决的阈值ε为0.50,采用基于BPAF(基本概率赋值)的决策。
(13)
通过图3(a)、3(b)、3(c)、3(d),可以看出来证据源的增加让系统识别更加可靠,其最终的融合结果如图上所示,可以看出来证据源的增加让系统更加可靠,融合结果更加准确。通过此判别方法,可知系统属于正常状态,与事实相符,方法可行。
当m2传感器数据异常时,使用决策层的融合结果与第一次融合判别状态相同,依旧准确,如图4所示。

图4 D-S数据融合
通过此模型,可以解决危化品运输车安全评价问题,并在数据融合时,解决了当部分传感器失灵时,系统的误判的问题。
4 结论
针对危化品运输安全预警模型,介绍了模型中的三种故障,以及使用的数据融合的理论基础,针对该理论中存在的基本概率赋值问题,选择使用专家知识和汉明距离的典型样本处理方法,而后搭建评价模型进行,并通过 MATLAB 仿真,可靠地解决了传感器异常时系统出现误判的问题。
——基于体育核心期刊论文(2010—2018年)的系统分析

