粒子群优化灰色模型在沉降预测中的研究

陈家骐，司大雄，丁 蕾，丁碧莹

(合肥学院 建筑工程系，合肥 230601)

基坑工程不仅要保证基坑本身的安全与稳定，更要有效控制基坑周边地层位移以保护周边设施的安全[1]。如今基坑的开挖深度越来越大，工程的地质条件越来越差，基坑距离周围建筑物或者市政设施越来越近，基坑工程事故不断发生。预测基坑工程周边地表沉降是基坑工程安全施工及周边既有建筑沉降安全评估的基础，准确有效地对基坑周边地表沉降预测和邻近建筑安全隐患的预警对安全文明施工有着重要的意义。邓聚龙于1982年提出灰色系统理论后，经过多年发展，已充分运用在各种安全预测领域[2-5]。其中DGM(1,1)模型的参数估计、数据拟合及预测均采用离散方程，不存在离散模型与连续模型之间的近似替代，具有较高的预测精度。但由于施工期间外界因素的扰动，沉降监测数据并不能完全反应真实的沉降规律，此外由于模型本身建模时迭代初始值使用缺陷，导致最终的预测结果与真实结果存在一定偏差。利用变权缓冲算子对原始数据进行新序列构造，可以有效地缓解外界因素的不良扰动，并运用粒子群算法对缓冲算子可变权重及新序列初始值的缺陷进行优化，快速搜寻到全局最优解，建立优化模型，提高预测精度。工程实例计算表明，二维粒子群优化DGM(1,1)模型能有效提高预测性能。

1 灰色预测模型

1.1 DGM(1,1)模型

定义1[6]：设序列X(0)=(x(0)(1),x(0)(2),…,x(0)(n))，其中x(0)(k)≥0,k=1,2,…,n.则称X(1)=(x(1)(1),x(1)(2),…,x(1)(n))为序列X(0)的一次累加生成序列，其中

(1)

定义2[7]：设序列X(0),X(1)如定义1所述，则称

x(1)(k+1)=β1x(1)(k)+β2

(2)

为离散灰色预测模型DGM(1,1)模型，或称为GM(1,1)模型的离散形式，其中β1，β2为估计参数。

定理1[7]：设X(0)为非负原始序列，

X(0)=(x(0)(1),x(0)(2),…,x(0)(n))

(3)

其一次累加1-AGO序列为

其中

X(1)=(x(1)(1),x(1)(2),…,x(1)(n))

(4)

(5)

对式(2)使用最小二乘法，则离散灰色预测模型的估计参数β1，β2满足

β=(β1，β2)T=(BTB)-1BTY

(6)

其中

定理2[7]：设B,Y,β如定理1所述，β=(β1，β2)T=(BTB)-1BT，取x(1)(1)=x(0)(1),则离散灰色预测模型的解为:

(7)

其中k=1,2,…,n-1

还原值为:

k=1,2,…,n-1

(8)

1.2 变权弱化缓冲算子

定理3[8]：设X=(x(1),x(2),…,x(n))为非负的系统行为数据序列，令

XD1=(x(1)d1,x(2)d1,…,x(n)d1)

(9)

其中，

x(k)d1=λx(n)+(1-λ)x(k)

(10)

其中，λ为可变权重，0<λ<1;K=1,2,…,n，当X为单调增长序列、单调递减序列或震荡序列时，称D1为变权弱化缓冲算子。

1.3 迭代初始值

且

(11)

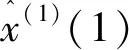
1.4 精度检验

1)平均相对误差α

(12)

2)后验差比C

C=S2/S1

(13)

S1为原始序列的标准差；S2为拟合序列与原始序列的残差序列的标准差。

3)灰色绝对关联度

(14)

(15)

(16)

2 粒子群算法优化模型

2.1 粒子群算法原理

假设在D维空间中有m个粒子，粒子i在D维空间的位置向量为xi=(xi1,xi2,…,xiD),粒子i在D维空间的速度向量为vi=(vi1,vi2,…,viD)。将粒子的空间位置向量带入目标函数f(x)求得适应值，根据适应度最大或最小准则判断该位置是否为最优位置，个体粒子i飞过的历史最好位置为pi=(pi1,pi2,…,piD),群体中所有粒子飞过的最好位置为pg=(pg1,pg2,…,pgD)[9]。粒子群算法中的粒子速度和位置按如下公式进行更新：

速度更新公式：

viD(t+1)=ω×viD(t)+c1×r1×(piD(t)-xiD(t))+c2×r2×(pgD(t)-xiD(t))

(17)

位置更新公式：

xiD(t+1)=xiD(t)+viD(t+1)

(18)

其中i=1,2,…,m

式中：t为迭代次数；viD为第i个粒子在第D维空间的速度；xiD为第i个粒子在第D维空间的位置；piD(t)代表第i个粒子在第D维中迭代t次时最好的位置pgD(t)代表粒子种群在第D维空间中迭代t次时最好位置；ω为惯性权重；c1是自我学习因子；c2是群体学习因子；r1,r2是[0 1]区间内的随机数。

2.2 粒子群算法的建模过程及参数设置

针对DGM(1,1)模型的不足，先后将式(10)与式(11)带入DGM(1,1)模型中构造优化DGM(1,1)模型，优化模型中的可变权重λ与修正系数β3作为待优化参数建立二维空间粒子群算法模型，以平均相对误差最小为准则，对缓冲算子的可变权重以及缓冲算子构造后新数据序列迭代初始值进行优化。

建模过程如下：

1)初始化设置。惯性权重ω取0.8；学习因子c1,c2在0到4之间，本算法模型取c1=c2=1.5;迭代次数t取值过大或过小会导致计算变慢或计算精度不足，本算法模型迭代次数选取t=100；优化DGM(1,1)模型中待优化参数λ与β3作为二维空间种群中的个体粒子，初始种群粒子个数取i=100；初始粒子的速度vi及位置xi用随机数函数给出。

2)适应度值计算。利用式(12)平均相对误差作为目标适应度函数分别计算适应度值。

3)个体极值与全局最优解。随机生成初始粒子λ与β3带入优化DGM(1,1)模型进行适应度值计算，采用式(17)和(18)更新粒子速度和位置。个体极值为每个粒子找到的历史上最优位置信息pbest，并从个体历史最优解中找到全局最优解gbest，并与历史最优解比较，选出最佳的粒子λ与β3作为当前的历史最优解。

4)循环迭代计算。以式(12)全局最小为准则，判断目标适应度值是否满足要求，如不满足要求则继续迭代计算直至满足最优准则或最大迭代次数。

5)计算结束。计算结束后得到优化DGM(1,1)模型最优参数参数λ与β3。

6)最终预测模型建立。使用求得的最优参数λ与β3构造优化DGM(1,1)模型，并利用该模型进行预测。

3 模型验证及工程应用

3.1 工程概况

地铁鸡鸣山路站车站为合肥市轨道交通4号线工程的第1个车站，车站有效站台中心里程为K1+280.000。车站主体为地下两层两跨岛式站台车站，结构形式为地下两层两跨/三跨/四跨矩形框架结构。车站主体采用明挖法施工，附属结构采用明挖法施工。围护结构采用钻孔桩+内支撑的支护体系。

3.2 分析预测

选取该工程周边地表沉降观测点DB2-1的等时距12期观测数据作为模型检测数据组。其中前10期数据作为原始序列利用章节2.2的方法建立二维粒子群优化DGM(1,1)预测模型，并对第11、12期数据进行预测，后2期数据作为检验数据与预测值比对，评估优化模型的预测性能。

利用表2中前10期数据分别带入传统DGM(1,1)模型和待优化的DGM(1,1)预测模型中。传统模型利用原始数据直接建模，待优化模型利用粒子群算法求得优化参数λ=0.0248，β3=-0.03512，利用优化参数构造二维粒子群优化DGM(1,1)模型。上述两种模型的模拟结果比对如表3所示。精度检验见表4。

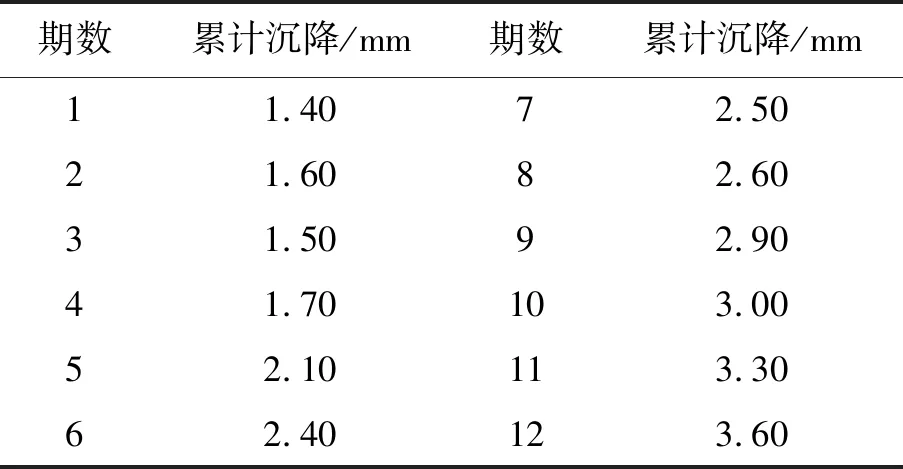
表2 测点DB2-1沉降观测数据

为了更加直观的看出传统模型和优化模型拟合预测性能的差别，将拟合结果及相对误差绘制如图1、2、3所示。

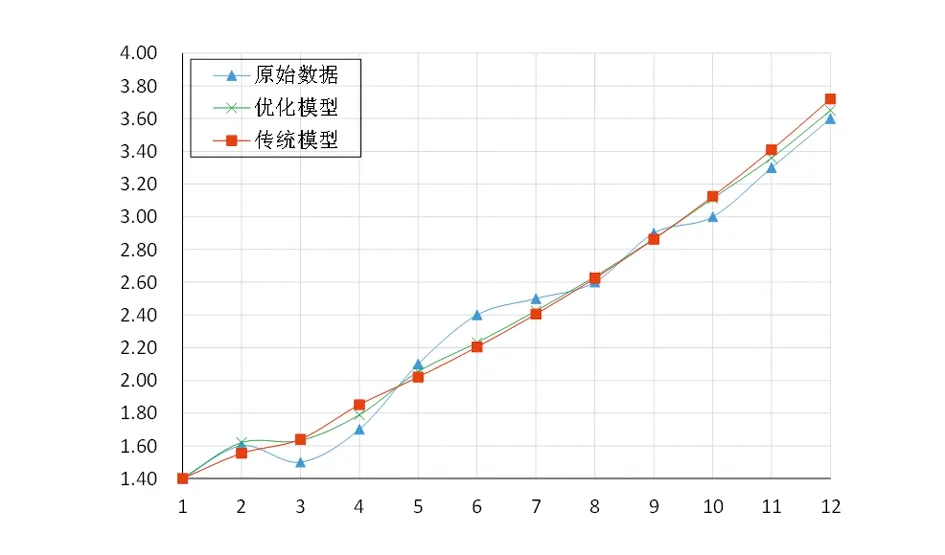
图1 模型拟合结果比对图

从图1中可看出，由传统DGM(1,1)模型所拟合的曲线相比于原始数据曲线，总体走势误差较大，第3、4、6、10期数据的偏差在图中可以明显看出。这由于传统DGM(1,1)模型中未考虑迭代初始值对模型本身的影响。由二维粒子群优化DGM(1,1)模型所拟合预测的曲线相比传统模型，因为考虑迭代初始值的作用，第3、4、6、10期数据的偏差相比传统模型显著减小，且作为检验数据的第11、12期数据，偏差均小于传统模型。

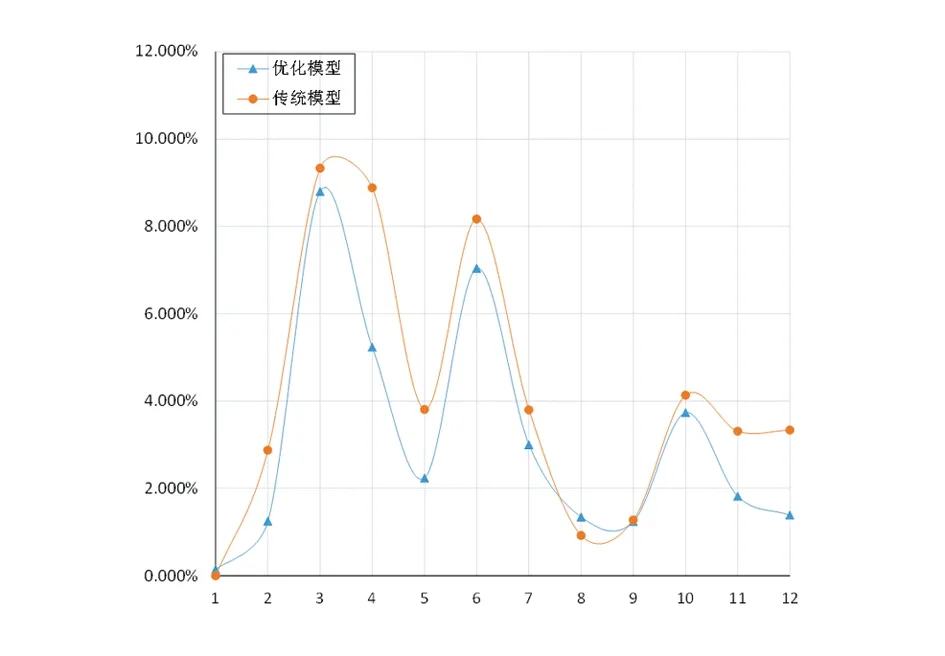
图2 模型拟合相对误差对比图

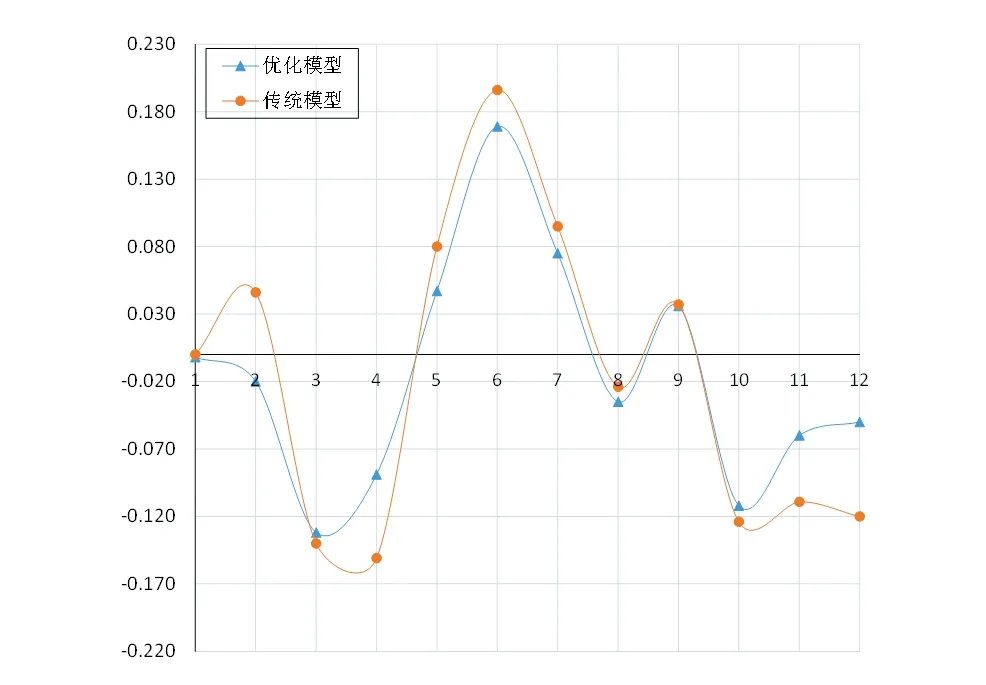
图3 模型拟合残差对比图

从图2和图3可看出，由优化模型所以拟合的曲线整体相对误差及残差波动小于传统模型，且由优化模型所预测的第11、12期数据的相对误差远小于传统模型。

由表3的拟合及预测数据可以看出，优化DGM(1,1)模型各期数据的残差及相对误差大部分小于传统DGM(1,1)模型。优化模型及传统模型在第3、4、5、6期的拟合数据出现较大的相对误差，原因是在这几期监测时段，监测数据受到外界不可控因素的扰动而失真，导致整个监测数据不能反映真实变化规律，出现拟合偏差。但优化模型受到缓冲算子的数据还原作用，使得预测第11、12期监测数据时，其预测值的相对误差只有1.82%和1.39%，残差绝对值为0.06和0.05，而传统模型第11、12期预测值的相对误差为3.31%和3.34%，残差绝对值为0.109和0.120。优化模型的残差绝对值远小于传统模型，而优化模型预测值的平均精度相比传统模型提高了约52%。

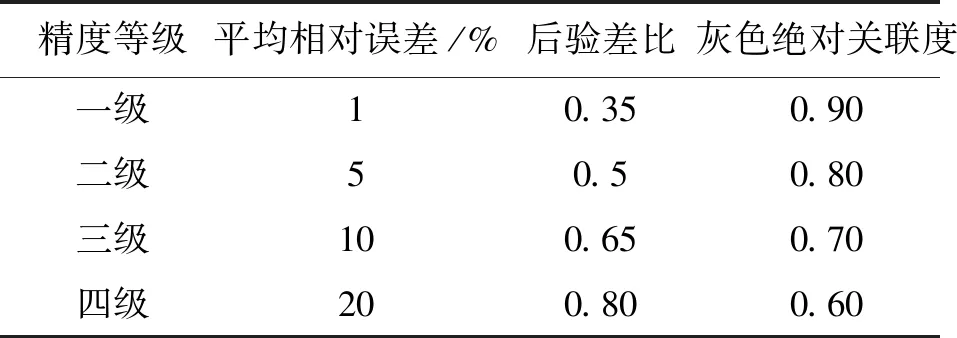
由表4的精度检验结果可知，传统DGM(1,1)模型和二维粒子群优化DGM(1,1)模型均有良好预测精度，其预测精度均为一级。优化模型的相对误差3.39%，相比于传统模型的4.53%，其预测精度提高了30%。优化模型的后验差比为0.12，相对于传统模型的0.17，预测性能提高42%。优化模型的灰色绝对关联度高于传统模型，说明利用优化模型拟合预测结果具有更好的有效性。

综上所述，传统DGM(1,1)模型与二维粒子群优化DGM(1,1)模型均具有良好的预测精度。但优化模型相比于传统模型，由于运用粒子群算法优化弥补了迭代初始值的缺陷，并用缓冲算子弱化外界因素对数据真实性的干扰，具有更高的预测可靠性及更好的模拟效果。

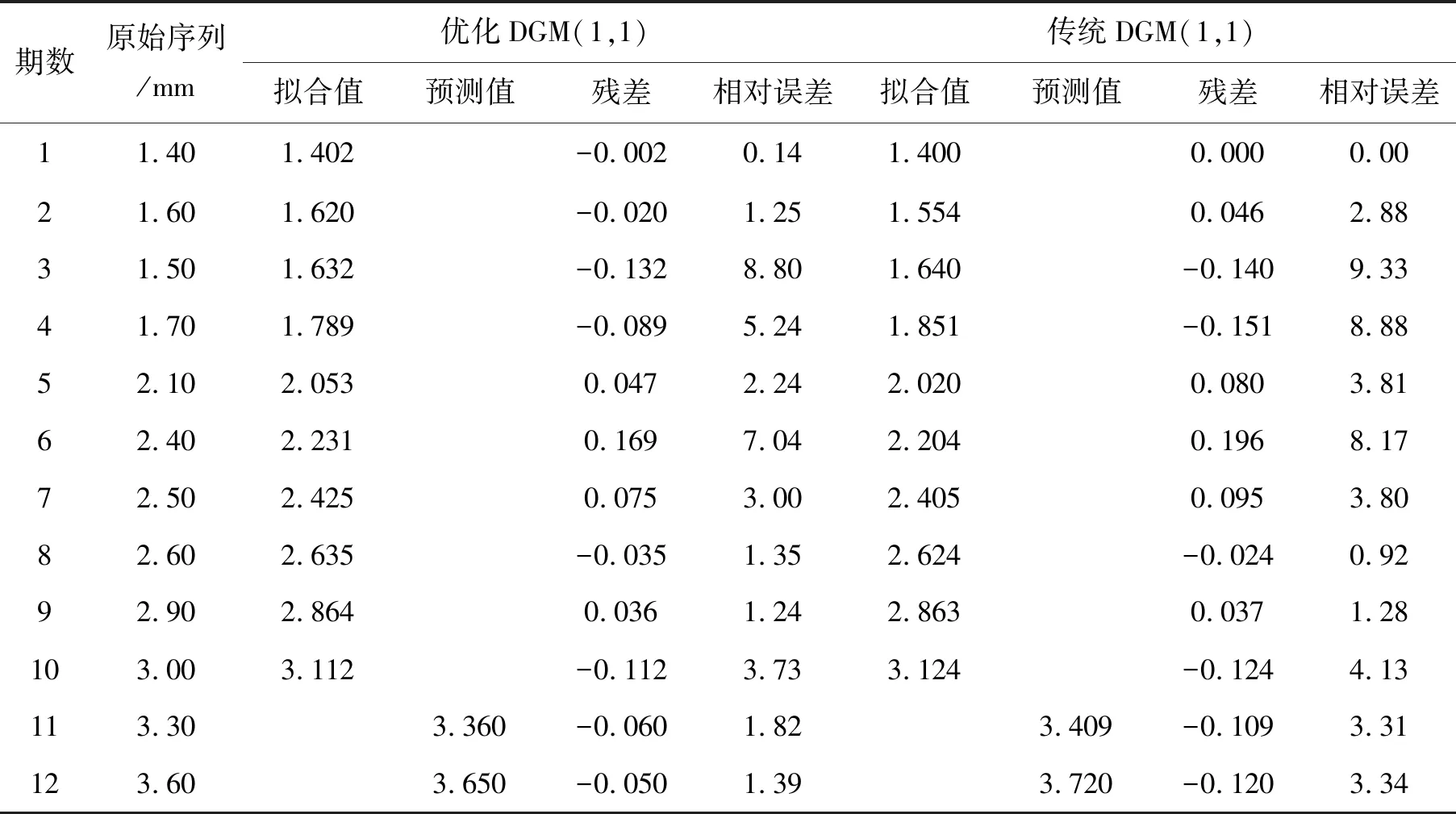
表3 模型拟合预测值

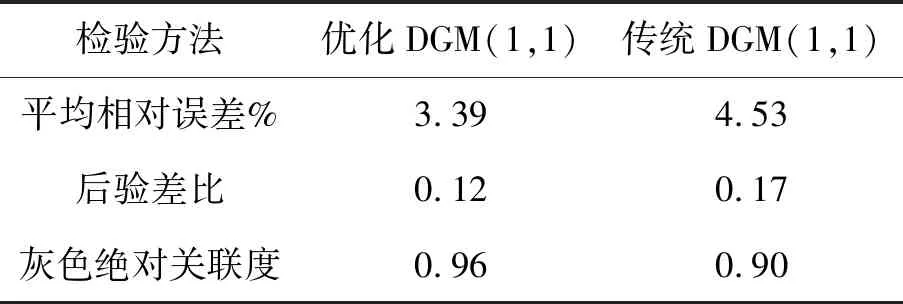
表4 模型精度检验

4 结论

运用粒子群算法对缓冲算子可变权重以及新序列初始值进行二维优化，进而提高了DGM(1,1)模型预测性能。将优化模型应用于基坑周边地表沉降预测领域，并得出以下3点结论：

(1)运用粒子群算法全局搜索快的特点对模型本身建模时迭代初始值缺陷进行弥补优化，解决最终的预测结果与真实结果存在偏差的问题。

(2) 运用变权缓冲算子对原始数据进行新序列构造，有效的缓解外界因素的不良扰动，并用粒子群算法搜寻最优权重。

(3)二维粒子群优化DGM(1,1)模型简单，易于施工人员掌握及运用，能准确有效的对基坑周边地表沉降进行预测，并为邻近既有建筑安全隐患的预警预报提供依据。