瞬变电磁发送机阻尼精确匹配方法

鲍明晖, 张民明, 李 波, 李军强, 周 密, 付志红

(1.重庆电力公司 电力科学研究院,重庆 401123; 2.重庆大学 电气工程学院,重庆 400044; 3.云南电网有限责任公司 电力科学研究院，云南 昆明 650217; 4.重庆璀陆探测技术有限公司,重庆 402660)

0 引 言

瞬变电磁法(transient electromagnetic method, TEM)又称为时间域电磁法,是一种地球物理勘探方法[1]。瞬变电磁探测系统主要由发送机、接收机以及数据处理软件组成,其基本工作原理是发送机通过不接地发射线圈向地下周期性地发送恒定幅值的电流脉冲,在地下建立一次脉冲磁场,当地下存在导电地质体时,一次脉冲磁场会在导电地质体中感应生成涡流,在脉冲电流关断间隙,接收线圈接收涡流产生的二次场,并对接收到的二次场数据进行分析处理,根据处理的结果便可得到地下的地质结构[2-5]。

理想情况下瞬变电磁发送机发射电流的波形为双极性恒幅矩形波[6],实际应用中由于负载为感性的线圈,发射电流下降沿通常呈指数形式下降,并且线圈自身存在自感和寄生电容,因此实际响应为典型的二阶欠阻尼响应,发射电流在关断末期不可避免地会出现过冲和震荡现象,这会严重影响二次场的早期信号,对后期数据处理也会带来不利[7]。为加快发射电流下降以及降低或消除发射电流震荡,目前应用较广泛的方案是在发射线圈两端并联一个阻值适当地吸收电阻配合恒压钳位技术,使响应变为临界阻尼响应,具体的阻值大小根据线圈自身参数的不同而异[8]。

1 恒压钳位高速关断原理

恒压钳位高速关断电路如图1所示,文献[9]指出采用此恒压钳位高速关断电路,在发射电流关断期间将负载两端的电压钳位在幅值较高的电压源上,可以实现调整电流下降沿的目的。图1中，虚线框1为钳位电路,虚线框2为可调恒压源。当正向供电截止,发射电流i0(t)开始下降时,电流通过负载L、D7、C1、D3形成续流回路,如果关断期间电容C1的电压值uC1保持恒定,即负载两端钳位电压值等于-UC1,那么发射电流将线性下降,且钳位电压越高,发射电流下降得越快。

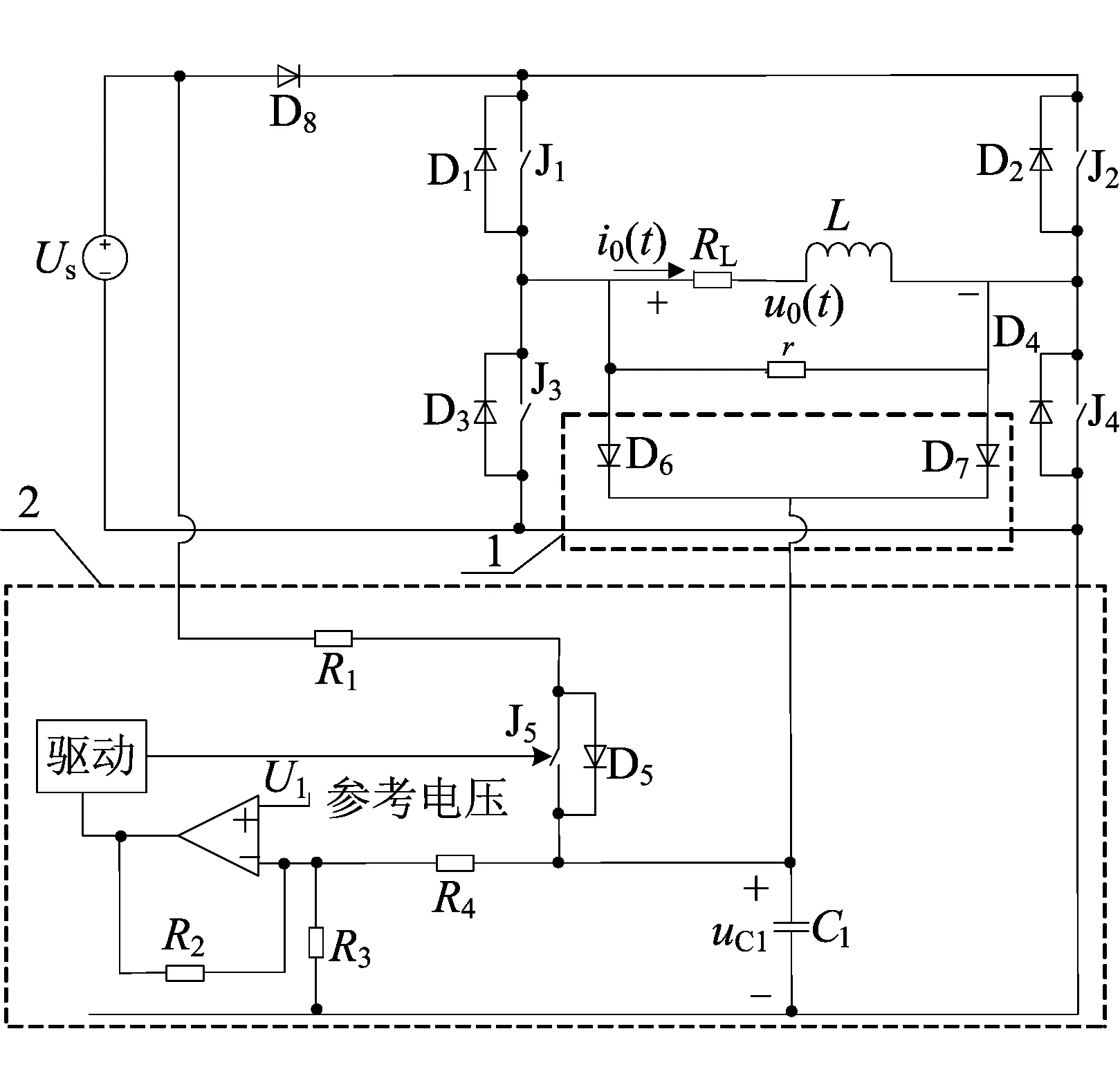
图1 恒压钳位高速关断电路

图1中,与负载并联的电阻r即为针对该发射线圈所匹配的阻尼电阻,当改变线圈匝数或更换线圈时,需要重新调整阻尼电阻阻值与之匹配,因此,实际应用难以实现最佳匹配。本文针对这一弊端,设计了一种精确匹配阻尼电阻的方法与装置。

2 阻尼电阻匹配

2.1 阻尼吸收的基本原理

瞬变电磁发射装置的发射线圈按尺寸大小可分为大回线和多匝小线框两类。多匝小线框线圈因其自身的一些特征,其等效电路模型不仅存在线圈电感和内阻,还存在匝间的分布电容,而分布电容和电感所形成的响应为典型的二阶响应。当发射电流突然关断,若仅在线圈两端接入恒压钳位电路而未加吸收电路,则在关断末期往往会出现电流过冲和震荡[10]。等效电路模型如图2所示。

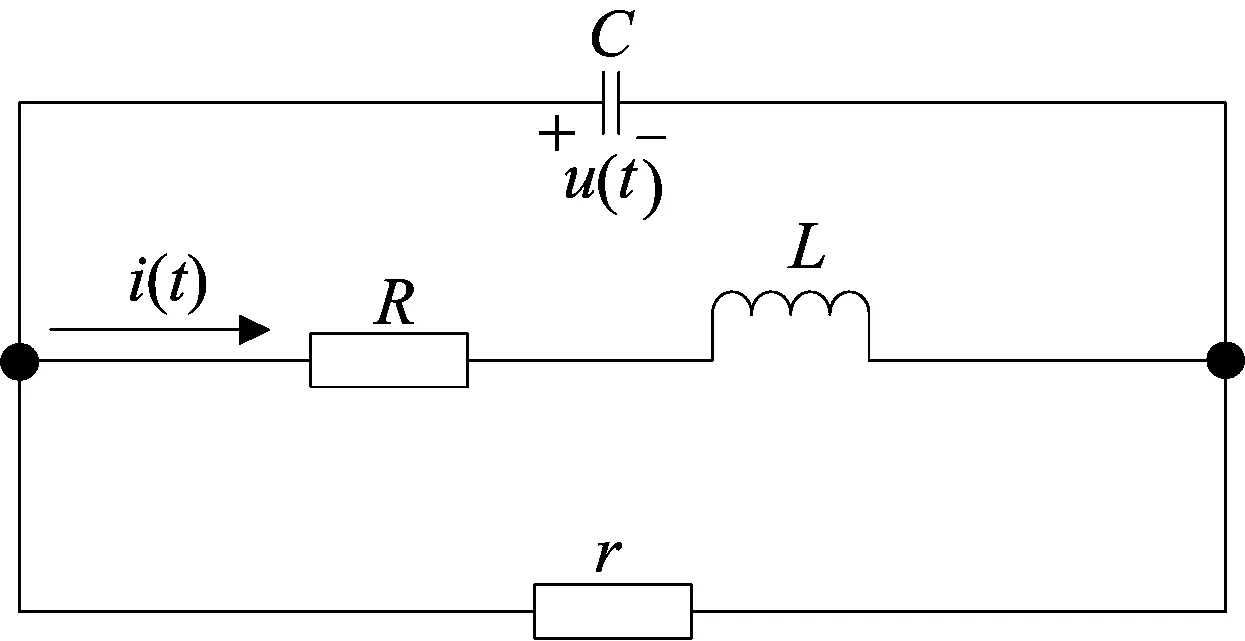
图2 发射线圈等效的分布参数电路模型

图2中,u为供以脉冲电流的发射线圈两端电动势;R为线圈内阻;L为线圈等效电感;C为发射线圈分布电容;r为并接在发射线圈两端的阻尼电阻。

由图2可知，该等效电路为二阶电路,可根据电路结构及基尔霍夫定律推出如下公式:

(1)

由(1)式可得,该模型的时间域表达式为:

(2)

(2)式可简化为:

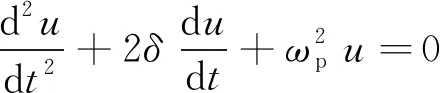
(3)

其中

其中,ωp、ω0为发射线圈谐振频率和固有谐振频率。

由此可知，发射电流的关断过程为二阶响应,二阶响应又可分为过阻尼、欠阻尼、临界阻尼3种状态,其中欠阻尼是存在震荡的暂态过程,过阻尼拖尾时间太长,而临界阻尼状态则可避免震荡。定义阻尼系数为:

(4)

当ζ>1时,为过阻尼响应;当ζ<1时,为欠阻尼响应;当ζ=1时,为临界阻尼响应。在Simulink中仿真的3种状态的归一化响应曲线如图3所示。

由(4)式可知,阻尼系数与线圈内阻、自感、分布电容以及匹配的阻尼电阻均有关,且若想达到临界阻尼状态,则所需的阻尼电阻阻值需随线圈的各项参数改变而改变。在使用多匝小线框时，为了减少干扰以及增加探测深度,通常需要增加发射线圈匝数来提高磁矩发射,而线圈的自感、内阻以及分布电容均与匝数存在联系,匝数改变,各项参数相应发生改变,因此之前所匹配的阻尼电阻便无法与新的线圈相匹配,此时若不改变阻尼电阻阻值,则所得到的响应将不再是临界阻尼响应,发射电流仍会在关断末期出现过冲和震荡现象。

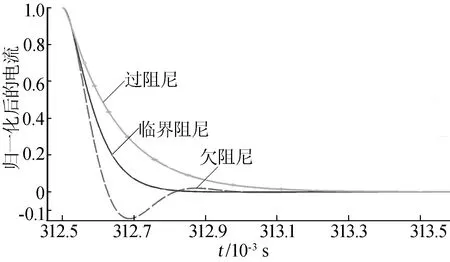
图3 各阻尼状态归一化响应曲线

2.2 线圈等效电路各参数的计算与实测验证

为实现阻尼精确匹配,需在事先对各规格发射线圈的等效参数进行求解,并将结果存储建表,用以作为后期调整匹配阻尼电阻时可供查询的原始数据。电阻的计算利用导线电阻的决定式,即

R=ρl/S

(5)

其中,ρ为线圈导线电阻率;l为导线长度;S为导线横截面积。

发射线圈电感参数的求解采用Kalantarov和Tseytlin在1955年提出的公式,即

(6)

其中,d为发射线圈直径;N为线圈匝数;μ0为真空中磁导率;Φ为随比值k变化的量(k=l/d),Φ的计算式参考短螺旋管线圈模型(k是小数值时),即

(7)

多匝小线框线圈的匝间分布电容是引起发射电流末端震荡的重要因素,其大小与线圈导线横截面积、绝缘层厚度以及线圈匝间距离均密切相关。特别是当发射线圈为匝间紧密结构时,2匝线圈之间的距离仅为绝缘层,故此时绝缘层厚度对分布电容的影响较大[11]。

N匝线圈匝间分布电容等效网络结构如图4所示。文献[11]指出多匝小线框每匝线圈均可等效为一个节点,采用麦克斯韦2-D静电轴对称求解器,利用有限元模型能快速地仿真计算出各点对点的电容值。经仿真计算得出各匝间寄生电容CM，N之后,运用Matlab软件通过适当的矩阵运算消除各中间节点,可得到2个终端节点之间总的等效分布电容C的值。

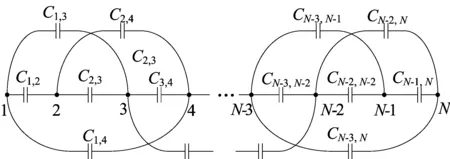
图4 匝间分布电容等效节点

发射线圈各参数的求解对实现阻尼精确匹配至关重要,为验证所采用计算方法的准确性,特对其进行实际测量,将测量值与计算值进行对比。

瞬变电磁发射机多匝小线框发射线圈各参数值的测量主要是考虑如何获得分布电容值,本文采用并联电路的电阻定律推得分布电容值[12-14]。具体方案首先是利用LCR测试仪测出单匝线圈的电感量L1及品质因数Q1,此时单匝线圈无匝间分布电容存在,则阻抗可表示为:

Z1=R1+jωL1

(9)

品质因数为:

Q1=ωL1/R1

(10)

由测出的L1和Q1及给定的激励频率,结合(8)式、(9)式可以求解得出R1。

当发射线圈为N匝时,此时的电路模型为电感和内阻串联再与分布电容并联,则阻抗可表示为:

(10)

可得:

(11)

N匝时品质因数为:

11 刘译：...and that their understanding of the Way is similar.[4]38

(12)

推导出分布电容C的计算公式为:

(13)

因此,由LCR测试仪测出N匝线圈的电感L和品质因数QN,再结合前面所得出的单匝线圈内阻R1求出内阻R,便可求解出分布电容C的值。

发射线圈有效面积固定为128 m2时,不同匝数规格的发射线圈各项参数计算值与测量值见表1、表2所列。

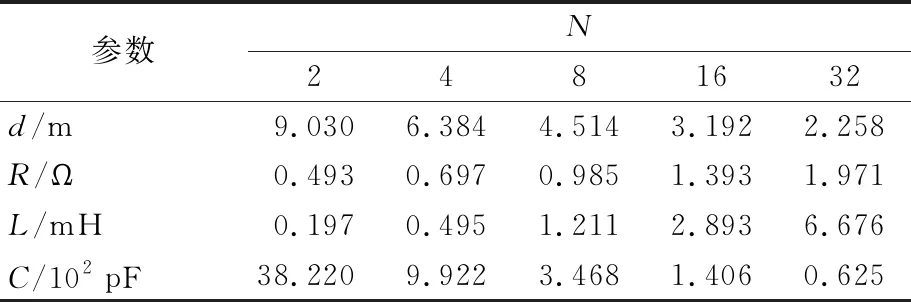
表1 发射线圈参数计算值

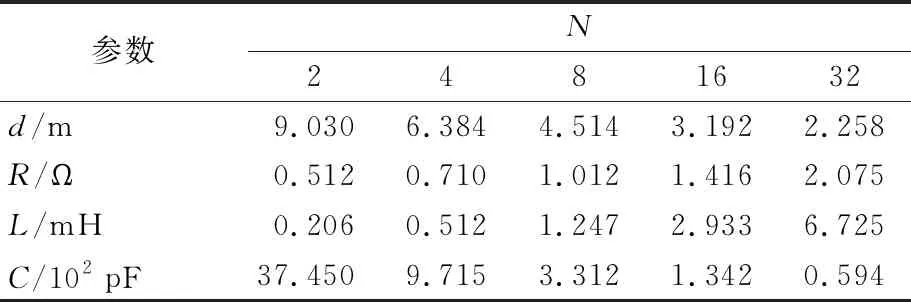
表2 发射线圈参数测量值

从表1、表2可以看出,发射线圈匝数增加时,线圈电感和内阻增加,线圈直径及分布电容减小,发射线圈参数的计算值和测量值相差不大,内阻、电感、分布电容3个参数的相对误差绝对值的平均值分别为2.97%、2.54%、3.81%,由此可见,所采取的计算方法在实际应用中可行。针对常用的各规格发射线圈,可在事先计算出其对应内阻、电感值及分布电容值的大小,将结果储存在计算机内，以作为现场应用时可供查表的原始数据来源。

2.3 阻尼匹配

结合(4)式的阻尼系数表达式，可得阻尼电阻为:

(14)

当ζ=1时,可得到临界阻尼响应抑制发射电流关断末期过冲及震荡现象,此时匹配阻尼电阻与发射线圈各参数的关系式为:

(15)

3 阻尼精确匹配调节方法

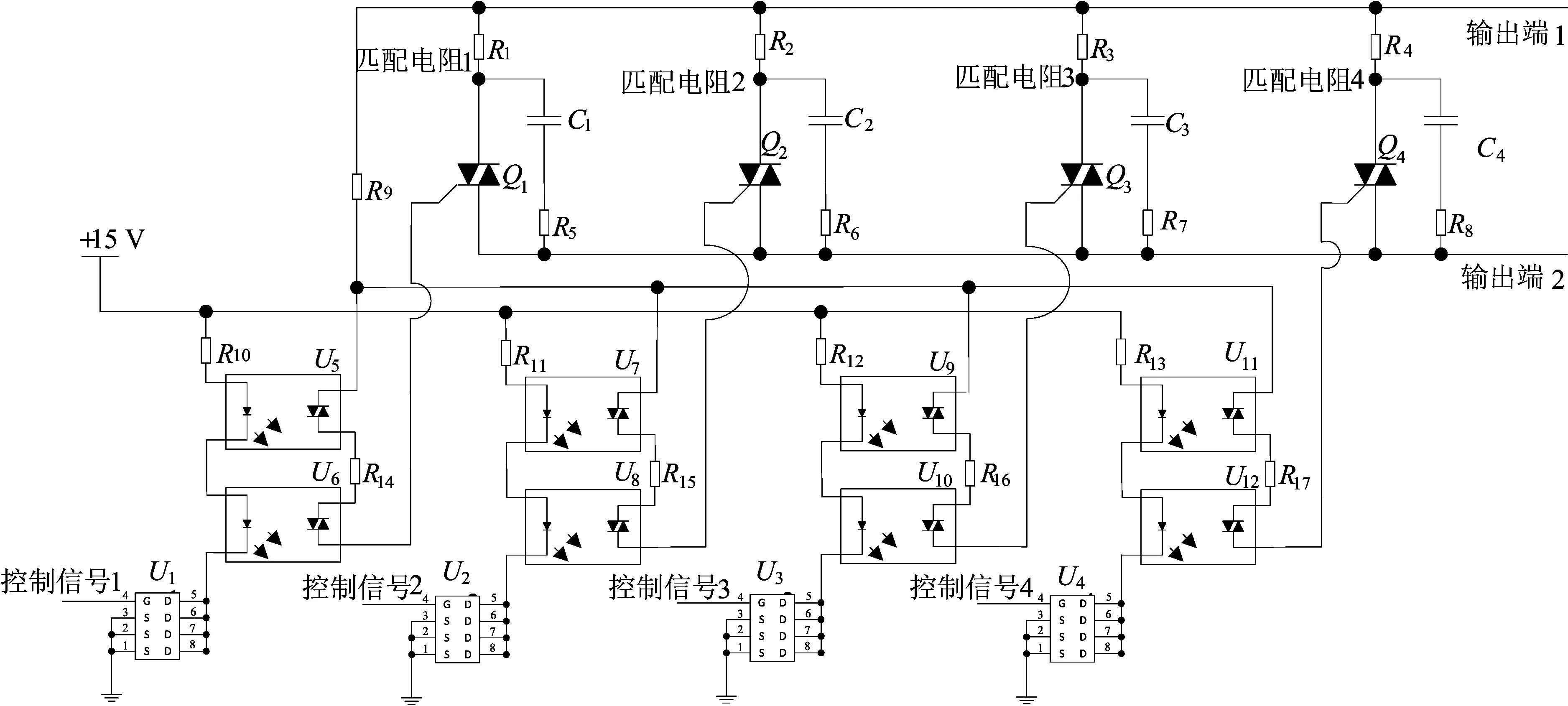
图5 阻尼电阻精确匹配装置

由图5可知,适配电阻R1～R4为可供选择的待接入阻尼电阻,输出端1、2接发射线圈两端,四路控制信号由计算机提供。当系统未检测到接入信号时,4个双向可控硅Q1～Q4均处于关断状态,此时四路阻尼电阻均与电容(C1～C4)、电阻(R5～R8)支路串联之后再并联接入发射线圈两端,由于C1～C4均是小电容,而电阻R5～R8均是阻值较大的电阻,则此时相当于接在发射线圈两端的是四路RC高频滤波电路,不会对发射线圈等效电路模型的响应性质造成影响;当选择接入阻尼电阻,如需接入R1,则计算机给场效应管U1开通信号,控制光电隔离器U5、U6导通,在电压过零点时刻驱动双向可控硅Q1开通,于是RC支路C1、R5被短接,阻尼电阻R1便可接入发射线圈两端,其余各支路阻尼电阻接入方法同理。当4个适配电阻选择的阻值互不相同时,可供接入的匹配电阻阻值可达16种组合。在实际应用时,本装置可根据更换后的发射线圈调用计算机内存储的各规格发射线圈参数数据,便可得知与之相匹配的临界响应阻尼电阻的阻值,再采用上述方法将其接入线圈两端。

4 实验结果

未匹配阻尼电阻、采用本装置精确匹配阻尼电阻时发射电流波形如图6所示。

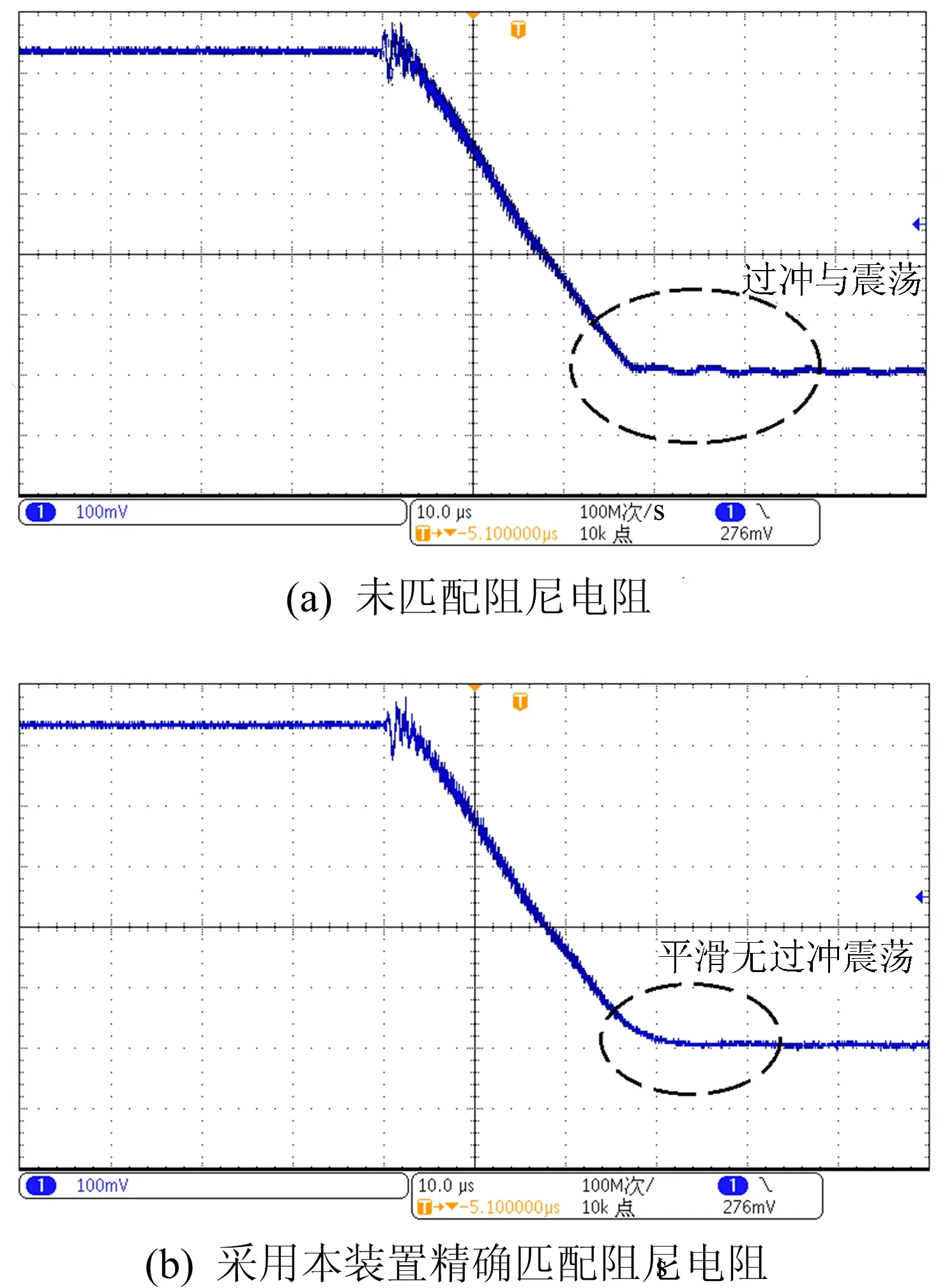
图6 未匹配及采用本装置精确匹配阻尼电阻时发射电流波形

为验证本装置的可行性,进行了2组对比实验。由图6a可知,在关断末期发射电流存在明显的过冲与震荡现象;由图6b可知,在关断末期发射电流平滑且无过冲。两者波形分别与图3中仿真得出的欠阻尼响应和临界阻尼响应的波形一致,从实验结果可看出，本装置对改善瞬变电磁发送机发射电流关断末期过冲与震荡效果显著。

5 结 论

本文提出了一种通过瞬变电磁发送机输出端口对不同发射线圈进行阻尼电阻精确匹配的方法。文中对发射线圈分布参数模型进行研究,获得了发射线圈自感、内阻及分布电容与达到临界阻尼响应时所需阻尼电阻的关系式,计算得出了各规格发射线圈的参数和对应的阻尼电阻值。实验验证采用本装置可实现根据对发射线圈规格参数的计算结果进行查表,驱动可控硅完成阻尼电阻的精确匹配接入,接入电阻后可有效改善发射电流关断末期波形过冲与震荡现象,弥补了当前瞬变电磁发射装置仅针对某一特定的发射线圈匹配了阻尼电阻,而在调整发射线圈后无法精确匹配阻尼电阻的缺陷。