一堂复习课的探讨与思考

裴 岚

（重庆市第四十二中学 重庆 400000）

笔者任教十年有余，有幸参加了一次区级展示课《二次函数图象与性质复习一》，借此展示课，做了一次大胆的尝试，感触颇深，现将这堂展示课呈现给大家，与各位分享、探讨。

一、课堂设计呈现

（一）初稿

【教学过程】

环节一、知识点复习：

①二次函数的一般式：_________其中二次项_________一次项________常数项_________在二次函数的定义中特别应该注意的是_________。

②二次函数的图象是_________，对称轴为_________，顶点坐标为 。

③二次函数顶点式为_____________，对称轴方程为_________，顶点坐标为_______ 。

对称性：轴对称图形，关于直线对称

增减性：a>0时，左↓右↑；a<0时，左↑右↓

开口大小：|a|越大开口越小

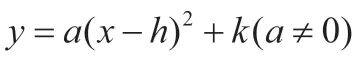
环节二、例题讲解：

（1）求当n为何值时，y为x的二次函数？

（2）求当n为何值时，y为x的二次函数且开口向下？

例2.二次函数y=-x2+4x-1图象的开口方向_______________，对称轴________，顶点坐标________。

例3.抛物线 的开口向________，对称轴是________ ，顶点坐标是________，是由抛物线向________平移_________个单位再向____________平移________个单位得到的。

环节三、考点精炼：

1.下列关于抛物线y=x2+2x+1的说法中正确的是（ ）

A.开口向下 B.对称轴为x=1

C.与x轴有两个交点 D.顶点坐标为（-1,0）

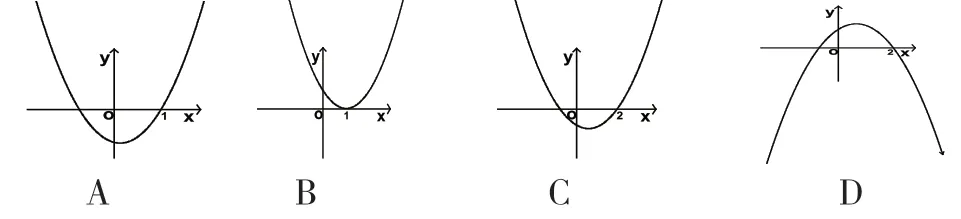
2.已知二次函数ax2+bx+c（a≠0）若a>b>c且a+b+c=0，则它的图象为（ ）

（二）定稿

【教学过程】

环节一、你说你画：

师：之前我们学习了二次函数的图象与性质，以及二次函数与一元二次方程之间的关系。今天我们一起来复习二次函数图象与性质。谁能列举一个只含二次项的二次函数呢？

学：y=2x2

师：你能画出这个二次函数的图象吗？

师：你能在此函数的基础上添加一项使其仍为一个二次函数吗？

学：y=2x2+1

师：你能画出此函数的图象吗？

师：能否在y=2x2基础上添加一个一次项呢？

学：y=2x2+2x

师：你能马上说出此函数的对称轴及顶点坐标吗？

师：我们有几种方法求解函数y=2x2+2x的对称轴及顶点坐标呢？

学：两种。配方法，公式法。

师：请同学们用配方法将函数y=2x2+2x转化为顶点式。

师：请同学们用公式法计算函数y=2x2+2x的顶点坐标。

师：函数y=2x2，y=2x2+1，y=2x2+2x有什么关系呢？可以通过怎样的平移得到呢？

环节二、我画你推：

图一：y=ax2+bx+c(a≠0)

图二：y=ax2+bx+c(a≠0)

师：你能从中获取到哪些信息？师：你又能获得哪些信息？

试一试：抛物线y=ax2+bx+c(a≠0) 图象的一部分如图所示。已知其对称轴为x=2与x轴的一个交点是（-1,0），下列结论中哪些是正确的？

①abc>0 ②4a-2b+c<0 ③4a+b=0

④抛物线与x轴的另一个交点为（5,0）

⑤点(-3,y1)，(6,y2)都在抛物线上，则有y1

师：同学们，今天我们从解析式到图象，又从图象得到解析式中各个系数的特征。二次函数的学习中数形结合是非常关键的，可以事半功倍。

二、同堂异构的经历与思考

初稿与定稿都是我自己的设计，显然初稿的设计比较保守，从知识点的梳理到习题的讲解与练习，每个环节都由老师设计好每一个步骤当然也包括习题的每一个系数.每一个字母，细致入微！这样的设计也是我从教以来的风格，很显然习题的设置立足于考试，从考点出发，其实显得很功利。在网络与科技如此发达的现在，我们这样功力的教学真的还适合学生、适合这个时代吗？在搜题软件满街都是的现在，我们到底应该教学生什么？什么样的教学才适合学生，适合这个时代？初稿的现场执教中，老师是主动地，学生是被动的，课堂是沉闷的。就象一场考试，老师出题学生答，并且答案唯一，课堂生成几乎没有，只有对与错，学生只是对知识点进行了复习与巩固，没有思维的发展，没有做到真正的倾听学生，表面的一问一答实际上只是“满堂灌”，课堂是无效的。如果一堂课只是让学生会做题，那么无论学生怎么学，都会败给搜题软件，我们的一堂课应该让学生的思维动起来，让同一课堂中不同程度的孩子的思维都得以发展。

定稿与初稿风格完全不同，从课堂开始就由学生自己搜索知识，此时没有唯一的答案，学生的思维是活跃的，没有答案可以抄袭，根据学生的答案再引出下一个环节，学生成为这堂课的主人翁意识油然而生，每个学生都会在课堂中得到不同的发展，都可以有自己的见解。现场执教中，课堂是活跃的，学生的答案是不统一的，这里没有对与错，学生是自由的，这样的设计不是学生跟着老师走，而是老师跟着学生走，学生是主动的，但是是有序地，学生与老师是相互牵制的结合体。例如当老师问道：你能列举一个只含二次项的二次函数吗？学生回答:y=x2；y=2x2；y=4x2等等， 是比较开放的。当然这种课堂老师的掌控能力的要求相对要高一点，更具有挑战性。