巧用弧的特征解决实际问题例讲
漆玉琼
(江西省宜春市宜阳学校 336000)
随着新课程的实施,中学数学的教学非常重视对学生独立思考、逻辑推理、数学应用等能力的培养,特别重视应用数学方法解决实际问题的能力的培养.几何中弧长与面积有关的计算题也是中考考查圆有关知识的重点,而且题型设计新颖、独特,常常结合实际生活中的实物为模型,考查学生数学建模的核心素养.
例1如图是一个桌面会议话筒示意图,中间BC部分是一段可弯曲的软管,在弯曲时可形成一段圆弧,设圆弧所在圆的圆心为O,线段AB,CD均与圆弧相切,点B,C分别为切点,已知AB的长10cm,CD的长为25.2cm.
(1)如图1,若话筒弯曲后CD与桌面AM平行,此时CD距离桌面14cm,求弧BC的长度(结果保留π);
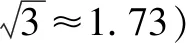
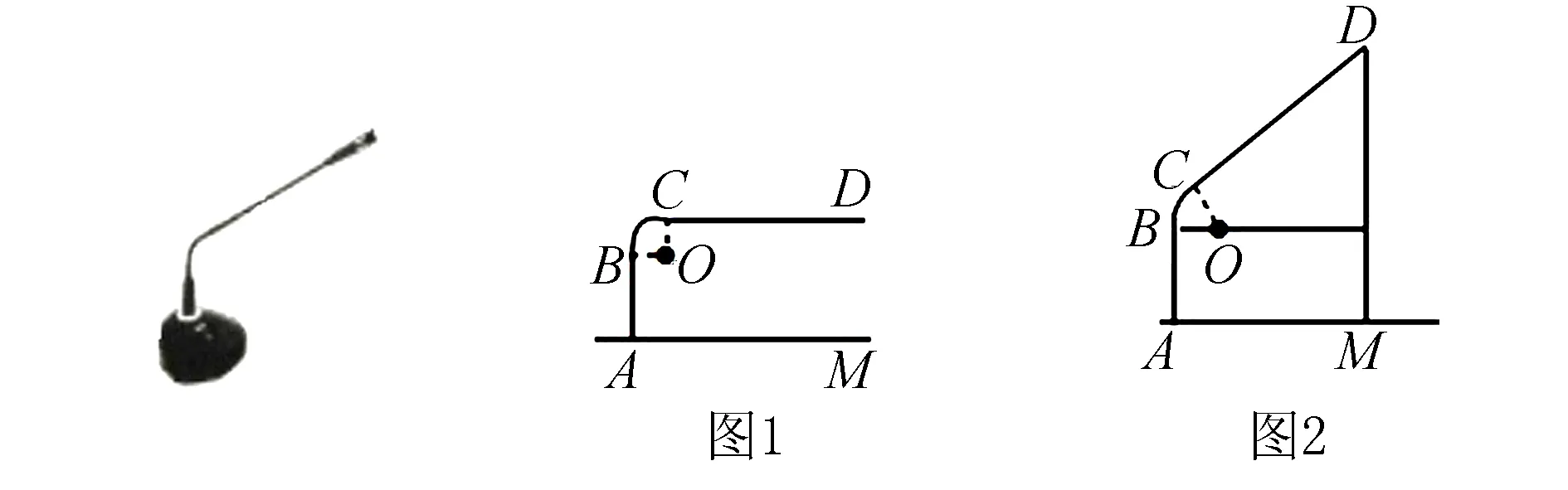
分析本题在第一问,由线段CD与AB平行的特殊情况入手,通过CD与AM距离探求获得弧BC的半径为4cm,圆心角为90度,然后可以直接利用弧长公式求出弧BC的长度.
解(1)如图1,∵线段AB,CD均与圆弧相切,∴OB⊥AB,OC⊥CD,
∴CD∥OB∥AM,∴∠BOC=∠OCD=90°.
∵CD距离桌面14cm,AB的长为10cm,
∴半径OC为4cm.
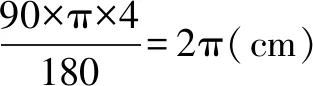
第二个图形由特殊化为一般情况,当弧BC的圆心角发生改变,此时要抓住弧的形状变了但是弧长不变,利用弧长公式可直接获得新弧的半径CO,再利用三角函数求出C点到BO的距离.
(2)过点C作CG⊥OB于点G.∵弧BC的长度为2πcm,
如图2,过点C作CN⊥DM于点N,则CN∥OB.
∴∠OCN=∠BOC=60°.
∵∠OCD=90°,∴∠NCD=30°,
∴DM=DN+CG+AB=12.6+5.2+10=27.8(cm).
∴话筒顶端D到桌面AM的距离是27.8cm.
本题有个易错点:很多学生误以为图1与图2中弧的半径不变而造成错误地求出点C到BO的距离,因此教师在引导学生分析时要尽可能使用直观教学,让学生找到题目中的变量与等量,从而正确运用条件求解.
例2(2018 金华)如图3是小明制作的一副弓箭, 点A,D分别是弓臂BAC与弓弦BC的中点,弓弦BC=60cm.沿AD方向拉弓的过程中,假设弓臂BAC始终保持圆弧形,弓弦不伸长.如图2,当弓箭从自然状态的点D拉到点D1时,有AD1=30cm,∠B1D1C1=120°.
(1)图4中,弓臂两端B1C1的距离为____cm.
(2)如图5,将弓箭继续拉到点D2,使弓臂B2AC2为半圆,则D1D2的长为____cm.
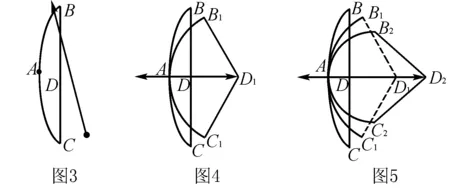
分析在(1)问中由AD1=B1D1=C1D1可知图形由弓形拉成扇形,在已知圆心角的条件下,利用直角三角形即可求出B1C1的长度.
解(1)连接B1C1,交AD1于E,则AD1垂直平分B1C1.
在Rt△B1D1E中,∵∠B1C1D1=120°,∴∠B1D1E=60°.

在(2)问中,图形进一步变化,扇形拉成半圆,图形由一般到特殊,此时弧B1AC1的形状变但是长度不变,从而可求出半圆的半径,进一步在直角三角形中可求出D2E,再获得AD2的长度从而解决问题.
(2)在题图2中,∵AD1=30,∠B1D1C1=120°,
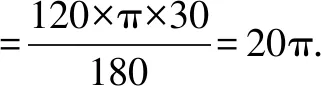
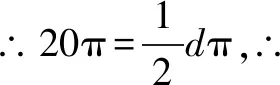
连接B2C2交AD2于E1,则AD2垂直平分B2C2,
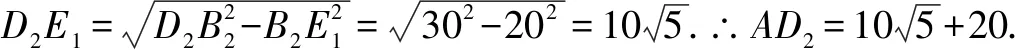
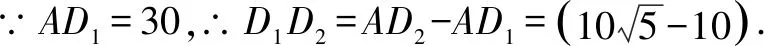
本题与例1有类似,同样是解题时要抓住弧BC的变化,由圆心角120度的弧变化成半圆后,弧长不变,但是半径也变了,所以需要通过弧长作等量可求出新弧形下的半径.在解题过程中仍然有不少同学误以为半径不变发生错误.
反思总结:以上两题无论是从一般到特殊,还是从特殊到一般,都是先通过已知条件易计算出该段弧的长度,再利用弧形变而弧长不变,再求出新的弧形下的半径,从而解决新的问题.其实质就是引导学生抓住变式前后的联系与区别,培养学生类比、联想、转化等数学思想方法的能力,让学生感受到数学推理的乐趣.

