分式优化问题的局部和全局最优性条件*

田超松，王仙云

(吉首大学数学与统计学院,湖南 吉首 416000)

许多实际问题,如资源分配问题、投资收益问题、生产计划和调度问题等,大都可以转化为分式优化问题,因而分式优化问题的研究受到学者们的广泛关注[1-8].特别地,如下带锥约束的分式优化问题引起了学者的极大兴趣：

s.t.x∈C,h(x)∈-S.

(1)

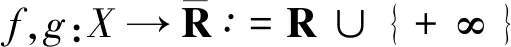
对于分式优化问题(1),通常借助Dinkelbach方法[1],将分式优化问题转化为如下约束优化问题进行研究[1-6]：

inff(x)-μg(x)

s.t.x∈C,h(x)∈-S,

(2)

其中μ∈R.显然,约束优化问题(2)与μ的取值有关.当μ>0时,问题(2)的目标函数f-μg为DC函数(即2个凸函数的差);当μ≤0时,f-μg为凸函数,问题(2)即为经典的锥规划问题.笔者拟分μ>0和μ≤0 2种情况进行讨论.在函数不一定下半连续、集合不一定是闭集的假设下,利用函数的次微分性质,分别引入新的约束规范条件,建立分式优化问题(1)的局部和全局最优性条件.

1 预备知识

设X和Y是实局部凸Hausdorff拓扑向量空间,X*和Y*分别表示X和Y的共轭空间,分别赋予弱*拓扑ω*(X*,X)和ω*(Y*,Y).x*,x表示泛函x*∈X*在点x∈X的值,即x*,x=x*(x).对于X的子集Z,用clZ和coneZ分别表示Z的闭包和凸锥包.进一步,若Z是X的子集,则用Z⊕表示Z的对偶锥,即Z⊕∶={x*∈X*:x*,z≥0,∀z∈Z}.用NZ(z0)表示Z在z0点的法锥,定义为

NZ(z0)∶={x*∈X*:x*,z-z0≤0, ∀z∈Z}.

令δZ表示Z的示性函数,

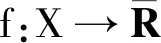
domf∶={x∈X:f(x)<+∞},

∂f(x)∶={x*∈X*:f(x)+x*,y-x≤f(y),∀y∈X} ∀x∈domf.

f*(x*)∶=sup{x*,x-f(x):x∈X} ∀x*∈X*.

特别地,由定义有NZ(x)=∂δZ(x),∀x∈Z.

由文献[9]中的定理2.3.1和定理2.4.2(ⅲ)可知,Young-Fenchel不等式和Young等式成立,即

f(x)+f*(x*)≥x*,x∀(x,x*)∈X×X*.

f(x)+f*(x*)=x*,x⟺x*∈∂f(x)⟺(x*,x*,x-f(x))∈epif*.

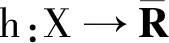
∂f(a)+∂h(a)⊆∂(f+h)(a) ∀a∈domf∩domh.

设φ:X→R∪{±∞}是一个实值函数,x0∈domφ且满足|φ(x0)|<+∞.定义函数φ在x0点的Frechet次微分为

显然,由定义可知

(3)

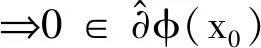
(4)

且

x0为φ的整体最优解⟺0∈∂φ(x0).

(5)

(6)

显然,h是S-凸函数当且仅当对于∀λ∈S⊕,λh是凸函数.

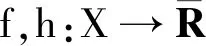
∂(f+h)(a)=∂f(a)+∂h(a) ∀a∈domf∩domh.

2 最优性条件

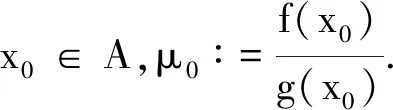
引理2[5]x0是问题(1)的最优解当且仅当x0∈A是以下问题的最优解：

inff(x)-μ0g(x)

s.t.x∈C,h(x)∈-S.

(7)

显然,问题(7)的目标函数f-μ0g的性质与μ0的取值有关.当μ0>0时,问题(7)的目标函数是DC函数;当μ0≤0时,问题(7)的目标函数是凸函数.因此,笔者对问题(7)分2种情形进行讨论.为了简便起见,记

(1)μ0>0的情形.

为了刻画问题(1)的局部和全局最优性条件,引入如下约束规范条件:

定义1(a)设x0∈dom(f-μ0g)∩A，若包含关系

(8)

成立,则称系统{f,g,δC;λh:λ∈S⊕}在x0处满足(FBCQ)条件.若对于∀x0∈dom(f-μ0g)∩A,(8)式成立,则称该系统满足(FBCQ)条件.

(b)设x0∈dom(f-μ0g)∩A，若等式

∂(f-μ0g+δA)(x0)=Ω(x0)

(9)

成立,则称系统{f,g,δC;λh:λ∈S⊕}在x0处满足(GBCQ)条件.若对于∀x0∈dom(f-μ0g)∩A,(9)式成立,则称该系统满足(GBCQ)条件.

注1当μ0=0时,(FBCQ)条件与(GBCQ)条件一致并转化为文献[9]中的(BCQ)f条件,即

(10)

命题1假设(BCQ)f条件成立,则系统{f,g,δC;λh:λ∈S⊕}满足(FBCQ)条件,从而

∂(f-μ0g+δA)(x0)⊆Ω(x0) ∀x0∈dom(f-μ0g)∩A.

(11)

定理1假设系统{f,g,δC;λh:λ∈S⊕}在x0处满足(FBCQ)条件.若x0是问题(1)的局部最优解,则对于∀β∈∂(μ0g)(x0),存在λ∈S⊕满足(λh)(x0)=0,使得

β∈∂f(x0)+NC(x0)+∂(λh)(x0).

(12)

证明假设系统{f,g,δC;λh:λ∈S⊕}在x0处满足(FBCQ)条件,即(8)式成立.设x0是问题(1)的局部最优解,由引理2可知x0也是问题(7)的局部最优解,故由(4)式可知

(13)

又由(FBCQ)条件成立，结合(13)式可得

(14)

(14)式意味着对于∀β∈∂(μ0g)(x0),存在λ∈S⊕满足(λh)(x0)=0,使得(12)式成立.证毕.

定理2假设系统{f,g,δC;λh:λ∈S⊕}在x0处满足(GBCQ)条件,则x0是问题(1)的全局最优解当且仅当对于∀β∈∂(μ0g)(x0),存在λ∈S⊕满足(λh)(x0)=0,使得(12)式成立.

证明假设系统{f,g,δC;λh:λ∈S⊕}在x0处满足(GBCQ)条件,即(9)式成立.由引理2和(5)式可知,x0是问题(1)的全局最优解当且仅当

0∈∂(f-μ0g+δA)(x0).

(15)

因为(GBCQ)条件成立,所以(15)式等价于0∈Ω(x0),即对于∀β∈∂(μ0g)(x0),存在λ∈S⊕满足(λh)(x0)=0,使得(12)式成立.证毕.

定理3设x0是问题(1)的全局最优解,则下列命题等价:

(ⅰ)对于∀β∈∂(μ0g)(x0),存在λ∈S⊕满足(λh)(x0)=0,使得(12)式成立.

(ⅱ)(11)式成立.

证明由定义可知,命题(ⅰ)成立等价于0∈Ω(x0).同时由(5)式可知,x0是问题(1)的全局最优解等价于0∈∂(f-μ0g+δA)(x0).证毕.

由命题1和定理1直接可得以下结论:

推论1假设(BCQ)f条件成立,若x0是问题(1)的局部最优解,则对于∀β∈∂(μ0g)(x0),存在λ∈S⊕满足(λh)(x0)=0,使得(12)式成立.

注2在假设f,g,h是真凸下半连续函数,C是X的非空闭凸子集的情形下,Sun等[5]利用闭性条件

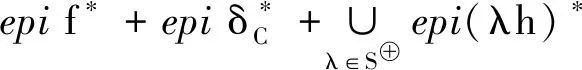
(16)

建立了当μ0>0时问题(1)的局部最优性条件.事实上,在此假设下,由文献[9]中的命题3.1和文献[10]中的推论3.4可知,(16)式严格强于(BCQ)f条件.于是,当(16)式成立时,由命题1可知 (BCQ)f条件成立.因此笔者改进了文献[5]中的定理3.2.

(2)μ0≤0的情形.

当μ0≤0时,问题(7)的目标函数f-μ0g是凸函数.由于凸函数的局部最优解即为整体最优解,因此现只考虑问题(1)的全局最优性条件.

定义2设x0∈dom(f-μ0g)∩A，若

(17)

则称系统{f,g,δC;λh:λ∈S⊕}在x0点处满足(CBCQ)条件.若对于∀x0∈dom(f-μg)∩A,(17)式成立,则称系统{f,g,δC;λh:λ∈S⊕}满足(CBCQ)条件.

注3当μ0=0时, (CBCQ)即为文献[9]中的(BCQ)f条件.

命题2假设(BCQ)f条件成立，设g在domf∩domg∩A上有连续点,则系统{f,g,δC;λh:λ∈S⊕}满足(CBCQ)条件.

证明假设(BCQ)f条件成立，即(10)式成立.设g在domf∩domg∩A上有连续点,因为f+δA和g都是真凸函数,所以由引理1可知

∂(f-μ0g+δA)(x0)=∂(f+δA)(x0)+∂(-μ0g).

于是,由(BCQ)f条件可知(17)式成立.

定理4假设系统{f,g,δC;λh:λ∈S⊕}在x0处满足(CBCQ)条件,则x0是问题(1)的最优解当且仅当存在λ∈S⊕满足(λh)(x0)=0,使得

0∈∂f(x0)+∂(-μ0g)(x0)+NC(x0)+∂(λh)(x0).

(18)

证明假设系统{f,g,δC;λh:λ∈S⊕}在x0处满足(CBCQ)条件，即(17)式成立.由引理2和(5)式可知,x0是问题(1)的最优解当且仅当(15)式成立.因为(CBCQ)条件成立,所以(15)式等价于

即存在λ∈S⊕满足(λh)(x0)=0,使得(18)式成立.证毕.

由命题2和定理3可直接得到以下推论:

推论2假设g在domf∩domg∩A上有连续点.若(BCQ)f条件成立,则x0是问题(1)的最优解当且仅当存在λ∈S⊕满足(λh)(x0)=0,使得(18)式成立.

注4在假设f,g,h是真凸下半连续函数,C是X的非空闭凸子集的情形下,Sun等[5]利用闭性条件(CC1)建立了当μ0≤0时问题(1)的局部最优性条件.事实上,类似于文献[9]中的命题3.1和文献[10]中的推论3.4可知,闭性条件(CC1)严格强于(CBCQ)条件.于是,当闭性条件(CC1)成立时, (CBCQ)条件成立.因此笔者改进了文献[5]中定理3.1.