基于车载全站仪免置平设站的轨道精测模型与算法

曹娟华，朱洪涛，吴维军，杨良根，陈志义，朱 嫣

(1.南昌大学 机电工程学院，江西 南昌 330031；2.江西制造职业技术学院，江西 南昌 330095；3.中国铁路哈尔滨局集团有限公司 牡丹江工务段，黑龙江 牡丹江 157000；4.南昌航空大学 飞行器工程学院，江西 南昌 330031)

在高速铁路建设和维护中，保证线路具有高定位精度和高平顺性精度是线路精测精调的核心[1]。基于CPⅢ控制网的客运专线轨道测量仪，通过测量轨道的三维坐标控制轨道绝对位置和线路线形[2]，通常被称为“绝对测量”，是轨道精调测量的主要手段和方法[3]。基于光纤陀螺惯性法的轨道检查仪，通过测量线路相对轨迹控制线路相对平顺性，通常被称为“相对测量”，主要用于超限检查、病害处理和轨道质量TQI评价[4]。由于绝对测量模式中短波平顺性测量精度有限，对于保证部分高速铁路±1 mm 的短波平顺性比较困难[5]，且数据采集时需要逐枕测量，测量效率低，约为0.2～0.3 km/h；而相对测量速度则快，约3～5 km/h，中短波平顺性精度高。因此，相对测量被引入高速铁路轨道精调测量中，相对+绝对复合测量模式也应运而生，测量效率为0.5～0.6 km/h，不但能控制线路的绝对位置，还能同时控制线路的长短波平顺性。所谓相对+绝对复合测量模式是采用轨道检查仪测量线路相对轨迹(陀螺仪自身漂移特性使相对轨迹随时间累积逐渐偏离实际曲线[6])，采用轨道测量仪按一定间隔测量轨道绝对位置偏差，如横向偏差、高程偏差等，作为相对轨迹坐标约束的边界条件，最后以离散傅里叶变换(DFT)和离散傅里叶逆变换(IDFT)进行两种测量数据的信息融合。

相对+绝对复合测量模式在数据处理方法上取得突破，达到较好的效果，但在测量环节，问题仍然存在：

(1)绝对测量精度有待提高。测量仪测量轨道三维坐标的方式仍然是全站仪在三脚架上置平、设站，然后测量小车棱镜[7]，设站方向角误差和棱镜测量时的测角误差同时存在，轨道定位精度与全站仪测量距离成反比，定位精度随着测量距离的增加而降低。

(2)绝对测量效率无法提高。为了保证轨道定位精度，必须对全站仪测量距离进行限制，每站最大测量距离只能达到80 m左右，每公里设站次数达到15次以上，操作人员工作强度和综合测量效率难以得到较大程度改善。

(3)测量过程中，以相对+绝对代替单独绝对，设备成本和人力成本增加。

(4)绝对、相对两种模式的里程测量方式不同，数据配准稍显困难，信息匹配度或受影响。

因此，在复合测量模式中，如何提高绝对测量部分的测量效率和测量精度，是一个关键而重要的问题。全站仪须先置平后设站和先设站后测量的测量方式是其测量效率低的主要原因。基于此，本文提出一种基于车载全站仪免置平设站的轨道精测方案：将全站仪安装于具有相对测量功能的轨道检查仪上，以实现相对+绝对测量系统在机械、电子、软件、信息及操作上的一体化。通过全站仪免置平设站模型和算法实现车载全站仪即停即设站，无需人工置平、人工搬站，求解非置平状态下的全站仪站点坐标，同时以设站点为小车特征点，结合小车姿态测量成果求解轨道中线三维坐标。其中，车载全站仪免置平设站和轨道中线三维坐标求解是本文的核心和重点。

1 全站仪免置平设站模型及算法

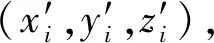
设全站仪在工程独立坐标系下的站点坐标为(Xs,Ys,Zs)，基于空间三维坐标转换模型，令矩阵Rr为空间坐标旋转矩阵，则

(1)

矩阵Rr中元素取决于全站仪的姿态，令全站仪坐标系x轴与水平面的夹角为ωx、全站仪坐标系y轴与水平面的夹角为ωy、全站仪坐标系x轴与工程独立坐标系正北方向在水平面上的夹角为ωφ，则

(2)

(3)

式中：

令观测个数n等于4，通过矩阵求逆，可求解X中的12个未知数

X=(B)-1Y

(4)

由于受观测条件、观测者、测量仪器等的影响，观测结果中必然存在观测误差，因此解算结果X也存在一定误差，我们将其称之为近似解，用X0表示。基于X0，得到各坐标观测值的误差方程

(5)

整理误差方程得到误差方程的矩阵形式

(6)

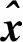
(7)

式中：P为权阵，全站仪对各CPⅢ控制点的测量是相互独立的，因此各点间的测量坐标是相互独立的。但同一控制点内的3个坐标是相关的，因此

(8)

其坐标值由全站仪测量的斜距S、水平角α、垂直角β计算得到，根据协方差传播定律和全站仪测量坐标的计算方法，得到全站仪测量坐标的中误差

(9)

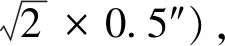
(10)

式中：ρ=206 225″。

以上公式中σ0均取1，最后，通过计算可得到全站仪免置平设站的站点坐标和旋转矩阵参数

(11)

2 “设站即测量”求解轨道中线坐标

当车载全站仪完成邻近的8个CPⅢ控制点的观测后，采用全站仪免置平设站算法，得到高精度的全站仪站点坐标，将其作为小车特征点，结合小车姿态测量成果，实现轨道中线三维坐标 “设站即测量”的一步法测量，见图2。

图2 车载全站仪测量系统数学模型示意

当轨道检查仪静置于轨道上时，以全站仪站点(Xs,Ys,Zs)为坐标系原点，建立独立的空间直角坐标系O′X′Y′Z′(以下称轨检仪坐标系)：以轨道检查仪侧臂所在方向为X′轴，轨道里程增大方向为X′轴正方向；以轨道检查仪横梁方向为Y′轴，指向侧臂的另一侧轨道；以X′轴和Y′轴正交方向为Z′轴，方向向上。则轨检仪坐标系下轨道中线的坐标为

(12)

式中：D为全站仪站点位置到轨检仪右轨作用边的横向距离；H为全站仪站点位置到轨检仪所在轨道面的垂向距离；g为轨检仪所在位置轨道的轨距测量值。

通过坐标旋转[11]，求解工程独立坐标系下轨道中线的三维坐标(Xc,Yc,Zc)：

(1)将轨检仪坐标系绕X′轴旋转α角(α为线路超高所形成的水平角，旋转后Y′轴平行于大地水平面)

(13)

(2)将坐标系绕Y′轴旋转β角(β为线路坡度角，旋转后X′O′Y′平面平行于大地水平面)

(14)

(3)将坐标系绕Z′轴旋转θ角(θ为线路方向角，旋转后X′轴指向正北方向)

(15)

(4) 将坐标系原点平移到工程独立坐标系(0,0,0)，平移量为(Xs,Ys,Zs)

(16)

对式(12)～式(16)进行整理，得到工程独立坐标系下轨道中线坐标

(17)

在轨道中线坐标(Xc,Yc,Zc)的计算中，将全站仪站点作为小车的特征点，从根本上实现了设站方向角误差和小车棱镜测角误差的零引入，是提高轨道中线坐标测量精度的核心。

最后，根据现有高速铁路轨道测量仪线路偏差计算方法[12]，结合线路设计线形，可计算线路横向偏差和高程偏差等轨道定位数据，用于陀螺仪相对测量轨迹的数据融合和轨迹约束，得到全线轨道数据。

3 线路试验

仪器：基于车载全站仪免置平设站的轨道精测系统样机1台，客运专线轨道测量仪1台，轨道对中装置1套，Leica TS60全站仪1套，Leica三脚架1套，Leica GPR121圆棱镜8套。

场地：带CPⅢ的高速无砟轨道线路；温度：27～31 ℃；气压：100.3～100.8 kPa;湿度：53%～68%。

3.1 定位精度

(1)选取具有直线、缓和曲线及圆曲线的试验线路900 m，分别在直线段、缓和曲线段和圆曲线段选取2个点作为待测点，各区段内2个待测点之间的间隔约为30 m，点号记为Z1、Z2、H1、H2、Y1、Y2。

(2)使客运专线轨道测量仪停处于Z1点，全站仪在距Z1点约10～70 m的范围内设站，测量Z1点处轨道的横向偏差和高程偏差。全站仪搬站，进行10次设站和轨道中线坐标测量，依据线路定位偏差计算方法，求横向偏差和高程偏差，记录于表1。同理，分别在直线段、缓和曲线段和圆曲线段进行10次设站，完成对Z2、H1、H2、Y1和Y2处轨道横向偏差和高程偏差的测量。

(3)采用基于车载全站仪免置平设站的轨道精测系统样机分别在各待测点处进行10次免置平设站，作为基础测量轨道的横向偏差和高程偏差。

为有效分析轨道测量仪和试验样机在实际测量中的有效观测精度，采用白塞尔公式计算各组观测值对应项目的测量中误差[13]。

(18)

式中：v为观测值与平均值之差；N为测量次数，N=10。

测量中误差计算结果如表2所示。

表2数据表明，现有轨道测量仪中线横向偏差和高程偏差的测量中误差与全站仪测量距离呈正相关，随着全站仪测量距离的增加，重复性精度降低；基于车载全站仪的轨道精测方法10次设站的位置都相同，各待测点的横向偏差和高程偏差的测量中误差变化不大，稳定性更好。基于车载全站仪的轨道精测方法，其横向偏差和高程偏差的测量中误差不大于0.5 mm，重复性精度更好。

测量重复性属于精密度的范畴，表示测量的再现性，是保证高准确度的先决条件，但是高的精密度不一定能保证高的准确度。因此，本文采用一套特殊的轨道对中装置和轨道中线测量方法对轨道中线横向偏差和高程偏差进行测量，将结果作为评价两种方法测量准确度的依据。

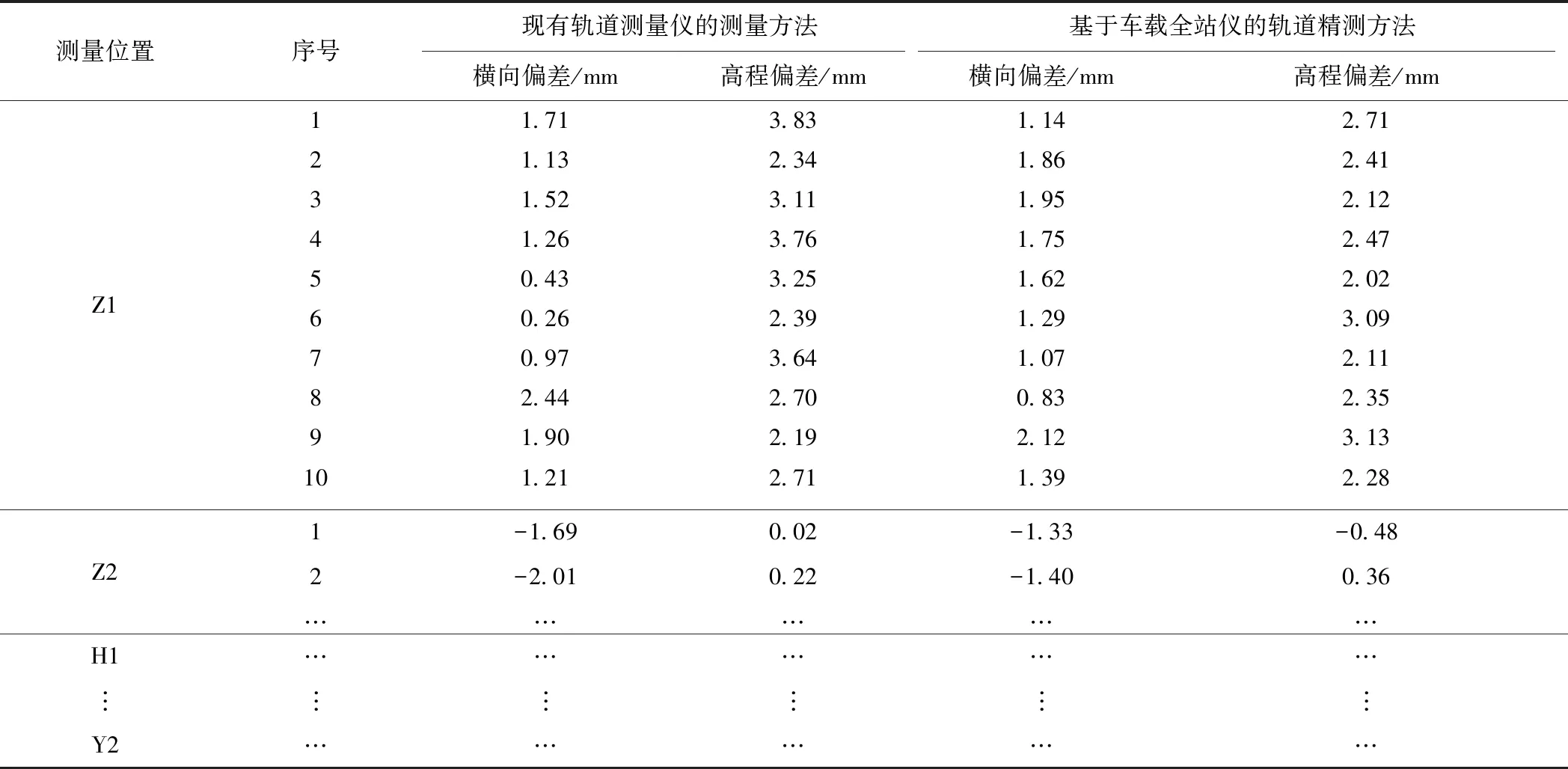
表1 线路试验测量数据

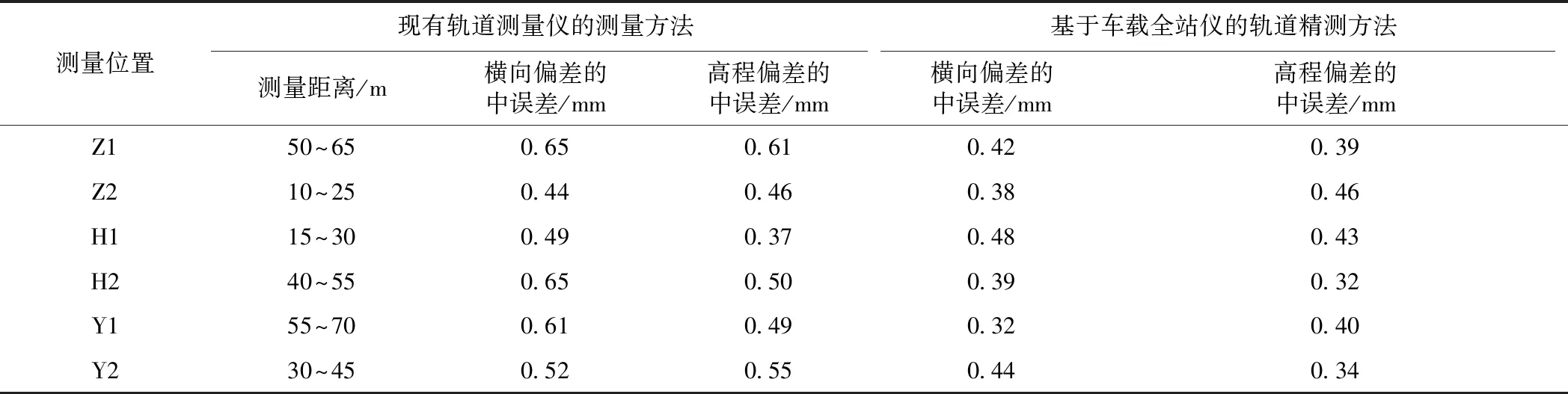
表2 测量中误差计算结果

轨道对中装置见图3，底座位于连杆中心，球形棱镜靠磁力紧吸于底座上，棱镜中心与轨道面等高。轨距测量轮在弹簧作用下，紧贴钢轨内侧，顶杆A和顶杆B机械上等长且位置对称，连杆绕固定于横梁的中心支点旋转，无论线路轨距如何变化，球形棱镜始终处于轨道中心位置。顶杆A和顶杆B的尺寸公差为0.01 mm，该装置对中精度较高。

图3 轨道对中装置的机械对中原理

将轨道对中装置放在轨道待测点处，采用Leica TS60全站仪在距离待测点约20 m处进行一测回置平设站，设站完成后采用一测回方式测量轨道对中装置上的球形棱镜，获得精度相对较高的轨道中线三维坐标，根据线路偏差计算方法得到轨道横向偏差和高程偏差。再次测量前，需要略微移动全站仪才能重新测量轨道横向偏差和高程偏差。最后，依次完成各待测点处轨道横向偏差和高程偏差的10次测量，并将10次测量结果的均值作为线路最或是值(最佳估计值)。

计算表1中线路试验数据与最或是值的差值，即横向偏差的似真误差Δh和高程偏差的似真误差Δv，然后计算两种测量方法的标准差M

(19)

式中：Δ为横向偏差的似真误差Δh或高程偏差的似真误差Δv；N为测量次数，N=10。

标准差计算结果如表3所示。

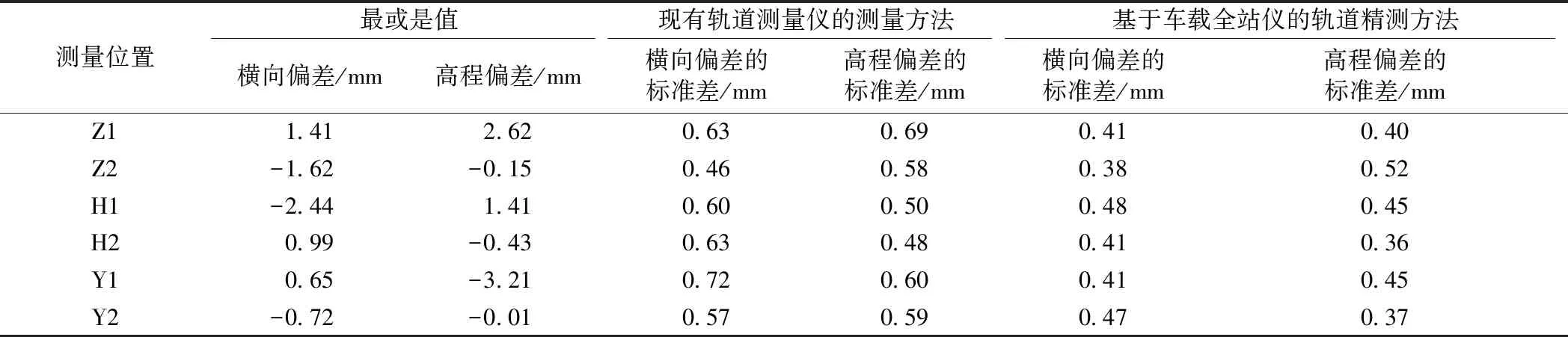
表3 标准差计算结果

由表3可知，无论是横向偏差还是高程偏差，基于车载全站仪的轨道精测方法的标准差都在一定程度上小于现有轨道测量仪的测量方法，因此，在轨道定位数据的测量准确度方面，基于车载全站仪的轨道精测方法优于现有轨道精测方法，其关键是新方法在设站后不再需要测量小车棱镜，设站的方向角误差和小车棱镜测量的测角误差不会被引入轨道中线坐标的计算中。

虽然基于车载全站仪的轨道精测方法在精度和稳定性方面表现更好，但值得注意的是，在其轨道精测中，特别是运营线路的轨道精测，控制点损坏的情况时有发生，控制点的数量和位置的布设将直接影响最终的测量结果。以某高速铁路K460—K480段线路试验为例，当控制点不足6个时，设站精度受到明显影响，同时，设站精度还受控制点位置分布的影响，应避免全站仪在离控制点过近(不大于5 m)的位置设站，以及避免全站仪一侧的控制点过于集中而另一侧的控制点很少的情况，必要时，应补测距离全站仪较远的控制点，以增加控制点数量和合理化控制点分布，从而提高轨道精测的精度。

3.2 测量效率

(1)选取具有直线、缓和曲线及圆曲线的试验线路900 m。

(2)单独绝对测量采集数据：采用高速铁路轨道测量仪采集线路定位数据，全站仪在三角架上设站后测量小车上的棱镜，全站仪每站测量距离10～80 m，每站搭接10 m，采用标准采样方式(逐枕)采集线路的横向偏差、高程偏差、超高偏差、轨距偏差等定位数据。

(3)相对+绝对复合测量采集线路数据：采用客运专线轨道测量仪按稀疏采样方式(8轨道板，约50 m里程间隔)采集线路定位数据；采用0级轨道检查仪测量线路，采集线路轨距、超高、轨向、高低等轨道内部几何状态参数。

(4)基于车载全站仪的轨道测量法采集线路数据：采用基于车载全站仪的轨道精测系统样机测量线路，采集线路轨距、超高、轨向、高低等轨道内部几何状态参数，按60 m里程间隔停一次进行车载全站仪免置平设站和轨道定位数据测量。

单独绝对测量需要逐枕测量，进行了14次设站，测量1 438根枕，约3.3 h完成，测量效率约为0.27 km/h；复合测量中相对测量时间为20 min，定位数据采集约为1.5 h，综合测量效率约为0.49 km/h；基于车载全站仪的轨道精测方法，全站仪每次免置平设站时间约为3 min，共进行了15次设站，包含相对测量推车时间，约63 min完成，综合测量效率约为0.86 km/h。3种测量方式的测量效率对比如表4所示，基于车载全站仪的轨道精测方法效率最高，比相对+绝对复合测量效率提高了75%。同时，基于车载全站仪的轨道精测方法仅用一套设备和一组人员，在一次操作中便实现相对+绝对测量，降低了设备成本和人力成本。

表4 综合测量效率对比

4 结论

针对相对+绝对复合测量模式中绝对测量部分测量精度有限、测量效率不高等问题，提出一种基于车载全站仪免置平设站的轨道精测方法，通过理论研究和线路试验，得到以下结论：

(1)全站仪免置平设站模型及其算法的实现是该轨道精测方法的核心；该方法打破了全站仪必须置平才能设站的传统，解决了全站仪安装在轨道检查仪上的技术问题。在新的系统中，不再需要三脚架和通信模块，结构更加紧凑，数据通信更加稳定。

(2)将全站仪设站点作为小车的特征点，采用轨道中线坐标设站即测量的方式，从根本上消除全站仪人工搬站这一环节，实现了设站方向角误差和小车棱镜测角误差的零引入。

(3)线路试验表明，基于车载全站仪的轨道精测方法测量稳定性好，横向偏差和高程偏差的测量中误差更小，精度更高。

(4)从测量效率分析，基于车载全站仪的轨道精测方法的综合测量效率达到0.86 km/h，比相对+绝对复合测量效率提高了75%。

全站仪免置平设站还需要依赖人工照准和测量，若进行测量自动化方面的研究，其效率将进一步得到提升。同时，设站间距是影响综合测量效率和测量精度的重要参数，如何以科学的方法求解最佳设站间距仍有待进一步研究。