改进的并联逆变器小信号稳定性分析方法

李 军，陈 杰,，邱瑞昌，徐春梅，刘志刚

(1.北京交通大学 电气工程学院，北京 100044；2.北京市轨道交通电气工程技术研究中心，北京 100044)

并联系统稳定性是考核并联系统的重要指标。对于大功率辅助并联系统，控制参数的改变对系统稳定性的影响非常大。因此，对并联系统进行稳定性分析是非常有必要的。并联系统稳定性分析需基于特定的并联控制策略，目前无互联线并联系统通常基于下垂法[1-8]，其主要思路是采用有功和无功功率对电压幅值和频率进行下垂控制，以实现自动均流。本文基于下垂法，并对其进行有效改进，提出一种全周期自适应的改进下垂法[9]，结合无需大延迟低通滤波器的新功率计算方法，能大幅度提升并联系统动态响应。建立一个并联逆变器的统一模型，通过数学工具对该模型进行分析，从而使并联系统动态响应得到提升在理论上被验证。

对于并联逆变器的数学模型，相关文献并不多。Coelho[10]等首次构建了并网逆变器的小信号模型，但只考虑了功率外环，而将电压内环视为理想状态。该方法较为简单，建立的模型为3阶，在一定程度上能反应单台逆变器的变化趋势。但该方法的缺陷在于将并联点电压视为独立变量，这对于并联逆变器而言自动屏蔽了另一逆变器对本逆变器的影响。文献[11-14]在本质上均是基于这种方法。Marwali[15]提出一种考虑整个并联系统的小信号模型建立方法，该方法将并联点电压表示为各逆变器的物理量，对一台逆变器进行分析的同时考虑了另一台逆变器的耦合效应，建立的模型更为准确。但其采用Z域下的离散方法建模，所建立的模型过于复杂，实际上由于并联系统中存在大延迟滤波环节，离散分析的意义不大，且这种方法没能考虑到功率计算方法的影响，所采用的下垂法在无互联线并联系统中也并不适用。

本文针对以上各方法的缺陷，提出一种全新的并联系统小信号模型构建方法，并在此基础上对并联系统进行稳定性和性能分析。该方法充分考虑到并联系统中各逆变器之间的耦合效应，并且将线路参数、负载特性、功率计算方法、低通滤波截止频率的影响均考虑在内，运用这种方法建立的模型能有效分析并联逆变器中各个相关量对系统性能的影响，具有广泛的适应性，并且本文所建立的模型相较文献[15]的模型更为简单。

1 并联逆变器控制方法

图1为本文所采用的并联系统拓扑，其中逆变器采用三相四线制分裂电容拓扑，每台逆变器分两级控制，分别为并联控制和逆变器控制，需要检测逆变器的每相输出电压和输出电流。图中，Udc1为直流侧电压，Lin为直流侧电感，iin为直流侧输入电流，Cin1、Cin2为直流侧支撑电容，f为支撑电容中点，uA、uB、uC为桥臂三相电压，iLa、iLb、iLc为滤波电感电流，L为逆变器滤波电感，r为逆变器滤波电感的寄生电阻，C为逆变器滤波电容，Ln为中线电感，in为中线电感电流，n为滤波电容的星型连接公共点，upa、upb、upc为母线三相电压，ioa、iob、ioc为逆变器滤波后的三相输出电流，erefa、erefb、erefc为并联控制的三相参考电压。

图2为逆变器控制原理框图，图中，Gv(s)为电压控制器传递函数，Gi(s)为电流控制器传递函数，iLref为电感电流参考值，iL为滤波电感电流，iC为滤波电容电流，tp为延时环节时间常数，io为逆变器滤波后的电流值。

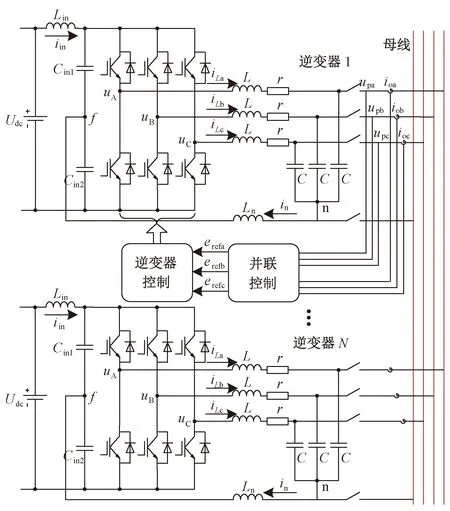
图1 并联辅助逆变器拓扑

图2 逆变器控制原理框图

根据该原理框图可以求得逆变器的输出电压为

uo=G(s)uref-Z(s)io

(1)

式中：

G(s)为逆变器电压指令的控制量；Z(s)为逆变器内阻。

式(1)表明逆变器的控制量和内阻均受电压控制器和电流控制器影响，如果选取合适的电压控制器和电流控制器，可对逆变器内阻进行准确设计。本文中电压控制器采用改进型谐振控制器，电流控制器采用比例控制器。

图3 逆变器内阻bode图

图3为逆变器内阻的bode图，从图中可见，采用图2所示控制方法的逆变器内阻呈现为阻性。因此，对于并联系统可以采用阻性下垂法。

(2)

式中：Eref为经过下垂控制环节的逆变器输出电压的参考电压幅值；φref为经过下垂控制环节的逆变器输出电压的参考电压相角；mp为有功比例下垂系数；md为有功微分系数；np为无功比例下垂系数；ni为无功积分系数；nd为无功微分系数。P和Q分别为有功功率和无功功率，为经过大延时低通滤波器之后的值。

传统上功率的计算方法为

(3)

令

(4)

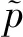
以上功率计算方法中，所求得的功率包含2倍基波频率的交流分量，因此需要大延时低通滤波器滤除其中的交流分量，这就降低了并联系统的动态特性。

为了改善并联系统动态特性，需将功率计算方法改进为

(5)

该方法需分别对电压电流进行延时90°，将付出较多的存储代价，但所求得的功率不包含交流分量，这使得低通滤波时截止频率可以设置较大，能够有效改善并联系统的动态特性，计算方法为

(6)

式中：ωc为截止频率。

2 传统小信号模型建立方法

图4 并联逆变器模型

根据前文的推导，可将并联系统简化为如图4所示的并联逆变器模型，Z1∠θ1、Z2∠θ2为逆变器输出阻抗，包括逆变器内阻阻抗和线路阻抗两部分。据图4，按复功率的概念可求得逆变器的输出功率为

(7)

(8)

式中：Uer为逆变器稳态时输出阻抗中的电阻电压幅值；Uex为逆变器稳态时输出阻抗中的电感电压幅值；U为逆变器稳态时的输出电压幅值。

考虑稳态值(φe，Ee，Ue)附近存在微小扰动，式(7)、式(8)可被线性化为

ΔP=ΔEα-ΔφEβ

(9)

ΔQ=-ΔEβ-ΔφEα

(10)

式中：

以式(2)的下垂法为基础求微分得

ΔE=-(mp+mds)ΔP

(11)

(12)

式(9)、式(10)经过低通滤波器后代入式(11)、式(12)得

(13)

(14)

化简式(13)、式(14)即可求得小信号模型为

s3Δφ+As2Δφ+BsΔφ+CΔφ=0

(15)

式中：

式(15)即为传统的小信号模型，可以发现其建模方法比较简单，所建立的模型为3阶，但这种建模方法并不准确，主要原因为：

(1)将并联点电压视为独立变量，消除了两台逆变器之间的耦合效应。然而对于实际的并联系统，两台逆变器之间必然存在耦合，一台逆变器的输出特性发生改变必然引起另一台逆变器的输出特性发生变化，因此传统小信号建模法的这种处理方法并不准确。

(2)负载特性对于并联系统稳定性有很大影响，但传统小信号模型却无法分析。

(3)传统小信号模型无法分析不同功率计算方法的影响。

3 新型小信号建模法

针对传统小信号建模法的不足，提出一种新的小信号建模法，该建模法所建立的模型具有足够多的信息量，既能分析控制系统电压环外的所有控制量又能分析电路参数的影响，并且所建立的模型较文献[15]中的模型更简单。

为便于说明，首先对图4所示的并联系统进行简化，见图5。这种简化只是为了建模和说明更简单，读者完全可以把逆变器输出阻抗和负载还原成任何特性，甚至可以考虑两台逆变器阻抗特性不一致对并联系统的影响。

图5 简化并联模型

由图5可得逆变器输出电流为

(16)

两台逆变器输出电流之和即为负载电流，通过负载电流可以求得输出电压为

(17)

将式(16)代入式(17)并化简得

(18)

由图5可知并联点电压相角为0。实际上并联点电压是正弦量，相角也是变化的，但是在此处为了建模方便将之设定为基准值，这样逆变器的相角φ1和φ2可理解为与并联点电压的相角差，而不是随时间变化的量。这种等效的意义在于将随时间的变化量转化不变量，可以进行小信号分析。

根据式(18)可得两组等式

(19)

0=E1sinφ1+E2sinφ2

(20)

式(19)规定了两台逆变器参数与并联点电压之间的关系，式(20)规定了两台逆变器稳态电压之间的关系，将式(18)代入式(16)可得

(21)

结合式(19)和式(22)、式(23)，可以求得传统功率计算方法的表达式为

(24)

式中：ai、bi、ci和di均可由逆变器参数表示。同理，根据相同的方法，可以求得新型功率计算方法，其表达式与式(24)相同，只是其中ai、bi、ci和di取值不同。

采用式(2)所示下垂法可得

(25)

对式(25)在稳态值(E1e，E2e，φ1e，φ2e)附近求微分可得

(26)

(27)

式中：D为系数矩阵,即

(28)

将式(27)代入式(26)即可求得并联系统小信号模型，见式(29)。

同理，可以构建基于新型功率计算法的小信号模型，模型仍见式(29)，只是系数略有不同。

(29)

式(29)所建立的模型为6阶系统，其物理意义是针对整个并联系统，而式 (15)所建立的传统小信号模型仅仅针对单台逆变器。式(29)的模型虽然较文献[15]的模型简单，但依然无法直接分析，需通过 Matlab求解计算。

4 并联模型分析

4.1 传统功率计算法小信号模型

首先分析传统功率计算方法所建立的模型，电路参数见表1，注意所取的稳态值需满足式(20)。

表1 电路参数表

图6为只采用比例下垂时传统功率计算法小信号模型的根轨迹图，图中蓝色线段代表根轨迹，黑色箭头代表根轨迹的变化方向(以下各图同)。图6(a)为ni=1，mp从0增加到1的部分根轨迹，图6(b)为mp=1，ni从0.01减小到0.000 01时的部分根轨迹。由图6可以发现采用传统功率计算法的并联系统在根轨迹上并不稳定，其原因为传统功率计算法会引入2倍频的交流量，为了抑制这部分振荡，可以增大mp或者减小ni。

图6 传统功率计算法小信号模型根轨迹图

图7 传统功率计算法小信号模型根轨迹图

图7为传统功率计算法小信号模型引入微分控制后的根轨迹图，下垂系数为：ni=0.001，mp=0.1，np=0.000 1，md=0.000 1，nd由0增加到0.008。由图7可见引入微分控制后增加了一对共轭复根，这是其动态响应提升的根本原因。

4.2 新型功率计算法小信号模型

从传统功率计算法建立的小信号模型可以看出，并联逆变器鲁棒性不强，为了对此进行改进，采用无需大延迟低通滤波器的新功率计算法，本文以基于新功率计算法建立的模型为主要分析对象。

图8为新功率计算法小信号模型只采用比例下垂时的根轨迹图。图8(a)为ni=0.000 1，mp由0增加到0.01的根轨迹，图8(b)为mp=0.000 1，ni由0增加到0.005的根轨迹。从图8可以得到：(1)新功率计算法相比传统功率计算法稳定性要更好，极点始终落在虚轴左侧；(2)只采用比例下垂时极点都落在负实轴变化，这说明只采用比例下垂的动态响应不高；(3)随着比例下垂系数的增大，系统极点左移，稳定性提高。

图8 新功率计算法小信号模型根轨迹图

图9为新功率计算法引入微分控制后的根轨迹图，从上到下依次是①、②、③、④，这4条曲线均关于实轴零线对称，分别对应ni=mp=0.1、0.01、0.001和0.000 1时nd由0增加到0.000 01的局部根轨迹图。由图可看出引入微分控制后产生了共轭复根，共轭复根的意义在于能提高系统动态响应，但是微分系数过大也会使系统不稳定。另外，在图9上还可看出比例下垂系数增大能使极点左移，提高了系统稳定性。

图9 引入微分控制后根轨迹图(np=md=0)

图10为新功率计算法小信号模型根轨迹图，图10(a)的控制参数1为：mp=0.01，ni=0.01，nd=0.000 000 5，md=0，np由0增加到0.000 1；图10(b)的控制参数2为：mp=0.01，ni=0.01，nd=0.000 000 5，np=0.000 05，md由0增加到0.000 1。图10(a)说明np的影响主要针对共轭复根，这说明可以修改np来微调系统动态响应。md主要影响在负实轴上的极点，但是这个极点不是主极点，对系统性能影响不大。

图10 新功率计算法小信号模型根轨迹图

图11给出了阻抗变化时的根轨迹图，下垂系数均为mp=0.01，ni=0.01，nd=0.000 000 5，np=0.000 05，md=0.000 000 01，图11(a)为Ro由0.01增加到100时的根轨迹，图11 (b)为Ro由0.001增加到0.5的根轨迹。图11 (a)说明随着电阻的增大，即负载减小，负实根上的极点分别向两边移动，但是主极点却离虚轴越来越近，说明负载变小的过程，系统稳定性也变差了。图11 (b)中随着逆变器输出阻抗的变化，虽然极点右移，但是主极点却一直未变，对系统影响有限。

图11 阻抗变化根轨迹

图12为低通滤波截止频率由0.01增加到20的根轨迹图，图中采用图11(a)和图11(b)中相同的下垂系数。说明增大截止频率在一定程度上可以系统更稳定，但是截止频率并不能无限制增大，当截止频率增大到一定程度，系统主极点变为随截止频率增大而右移的一对共轭复根时，系统稳定性就将变差。

图12 ωc变化根轨迹

5 结束语

本文的目的在于建立一种能详细分析并联系统中各参数对系统稳定性和动态特性影响的方法。传统的分析方法基于小信号模型，但是传统的小信号建模法所建立的模型并不准确，没有考虑到并联逆变器之间的耦合关系，无法分析特定功率计算方法的影响，无法分析负载影响，也无法分析逆变器输出阻抗的影响。本文提出的小信号建模法，以整个并联系统为研究对象，包含逆变器电压环以外的控制系统信息以及电路参数的影响，提供了一种到较为全面的分析方法。