基于动态面方法的高速列车蠕滑速度跟踪控制
徐传芳,陈希有,郑 祥,王 英,李卫东
(1.大连理工大学 电气工程学院,辽宁 大连 116024;2.大连交通大学 电气信息工程学院,辽宁 大连 116028)
高速列车的安全运行需要可靠稳定的牵引力和制动力,牵引力和制动力的形成主要依赖于轮轨间的黏着,而黏着关系是一个具有非线性、不确定性和时变性的复杂问题。黏着力的大小由轮轨间的黏着状态决定,受到轨面条件、环境气候和列车运行状况等诸多因素的影响。列车跟踪预期运行状态时,若牵引力或制动力超过轮轨间最大黏着力,则牵引力或制动力与黏着力之间的平衡关系就会被打破,列车所具有的多余能量会使轮轨间出现相对滑动现象,即出现车轮空转或打滑现象。采取合理有效的黏着防滑控制策略,可避免高速列车牵引和制动过程中的空转和打滑现象,保障列车的行车安全。
鉴于黏着控制问题的重要性,诸多学者进行了一系列颇有成效的研究。针对黏着力最大控制问题,文献[1]基于模糊逻辑参考蠕滑率生成算法,设计自适应滑模制动控制策略,可获得各种路况下的最大黏着力,改善车辆的制动性能;文献[2]通过调整工作点接近车轮蠕滑速度与牵引电机转矩电流之间特性曲线的峰值点,提出一种可以寻找轮轨间切向力峰值的防空转控制方法;文献[3]提出高速列车的鲁棒自适应再黏着控制策略,能自动调整控制转矩,快速驱动列车远离滑动区域,进入安全运行区域并尽量接近最优黏着点;文献[4]借鉴太阳能发电中的MPPT(Maximum Peak Power Tracking)方法,提出基于P&O(Perturbation and Observation)的新颖黏着控制算法,可得到电力机车加速模式下的最大黏着系数,获得列车的最大加速度。
当高速列车运行在风霜雨雪等不利环境、快速加速或紧急制动情况时,黏着力最大控制问题的研究具有重要的意义。而通常在良好的运行环境下,并没有必要获取最大黏着力。在保证防止车轮滑动的前提下,提供满足牵引力和制动力要求的黏着力也是一个应该关注的重要问题。为能够得到满足牵引力和制动力要求的黏着力,很多学者提出了针对期望蠕滑率进行精确跟踪的控制算法。文献[5]采用鲁棒自适应容错控制算法,通过调节实际蠕滑率跟踪参考蠕滑率,实现了高速列车的黏着防滑控制。文献[6]提出基于自适应神经网络控制的高速列车防滑制动控制方法,通过高精度的蠕滑率跟踪控制,保证列车获得大的黏着力及良好的制动性能。文献[7]考虑防滑限制,设计基于障碍Lyapunov函数(BLF)的蠕滑率跟踪控制方法,可在防止车轮滑动的同时,确保牵引与制动运行稳定。然而,蠕滑率与列车状态构成的非线性函数存在固有奇点,从而可能导致控制算法中的盲点,影响控制效果,使得利用蠕滑率来表现蠕滑的方式在高速列车黏着控制算法设计中并非合适的选择[8]。为此有些学者基于蠕滑速度跟踪进行黏着防滑控制算法的设计。对基于蠕滑速度跟踪,文献[9]提出高速列车的自适应主动黏着防滑控制算法,文献[10]提出自适应补偿控制的黏着防滑控制算法。然而文献[9]在高速列车动力学模型的建模过程中并未考虑牵引与制动转矩产生过程;文献[10]考虑了转矩产生过程,但并未考虑系统在蠕滑速度跟踪过程中的瞬时性能,虽然可以实现对期望值的精确跟踪,但并不能确保跟踪过程中不发生车轮滑动现象。
针对高速列车能在主动防滑条件下,获得满足牵引力和制动力要求的黏着力问题,本文建立了考虑牵引与制动转矩产生过程的高速列车动力学模型,并将黏着控制问题归结为含输出约束的非线性系统的控制问题,提出了高速列车蠕滑速度的动态面跟踪控制算法,并进行了证明。本文在策略中采用了在高速列车黏着控制运用中尚不多见的动态面控制DSC(Dynamic Surface Control),避免了常规反步控制中需要对虚拟控制量多次求取微分的困难[11]。未知参数通过自适应更新律估算,未知时变的黏着力和运行阻力由力观测器估计得到[12],引入BLF实现对蠕滑速度的上界约束[13]。仿真结果证明,本文算法实现了蠕滑速度跟踪控制误差的半全局一致最终有界,可使黏着工作点始终保持在稳定区域,防止由于控制过程中的瞬态响应问题而出现的车轮空转和打滑现象,实现全局主动黏着防滑控制。
1 高速列车动力学模型描述
1.1 考虑转矩产生过程的高速列车动力学模型描述
考虑高速列车车辆的1/4模型,并忽略牵引电机-轮对间的转矩传输动态,车体及车轮的动态方程可以表示为
(1)
(2)
式中:M为对应模型的列车质量;v和ω分别为列车车速和车轮角速度;J和r分别为车轮的等效转动惯量和半径;B为车轮的黏滞摩擦系数;Tn为牵引电机输出转矩(列车牵引转矩或制动转矩);Fa和Fr分别为列车的轮轨黏着力和运行阻力。
高速列车的运行阻力Fr包括列车运行过程中所受到的空气阻力和轨道阻力,表示为
Fr=a0+a1v+a2v2+o(·)
(3)
式中:a0,a1,a2为正数,其数值由具体的运行环境决定;o(·)为由轨道引起的随机不稳定阻力干扰。
轮轨黏着力Fa是与列车轮轨接触面实时状况有关的复杂函数,其表达式为
Fa=μ(λ)Mg
(4)
式中:g为重力加速度;μ(λ)为黏着系数,是蠕滑率λ的非线性函数,国内外应用较为广泛的是Burckhardt模型[14],其表达式为
(5)
式中:b1,b2,b3为正数,不同的参数表示不同的轮轨黏着条件;蠕滑率λ∈[-1,1],表示轮轨之间微量滑行的程度,其定义为
(6)
以往大部分文献通常忽略转矩产生过程,认为Tn即为系统的控制输入。考虑牵引与制动转矩产生过程更符合实际情况。由于电机的电磁时间常数远远小于列车的机械时间常数,因此没有必要考虑转矩产生的具体细节,其过程可以近似用一个简单的线性方程来描述[10],牵引与制动转矩的动态响应可以表示为
(7)
式中:Tz为期望的电机转矩,为控制变量;α,β为已知或未知常数。
由式(1)、式(2)和式(7)可得
(8)
(9)
1.2 防滑约束问题描述
高速列车的黏着特性具有高度非线性,不确定性和随机性等特点。图1为干燥和潮湿轨面条件下的黏着特性曲线。可以看出,牵引与制动过程的黏着特性机理是一致的。在蠕滑区范围内,黏着系数随着蠕滑率的增大而逐渐增大,直至峰值;当蠕滑率超过峰值,进入滑移区后,黏着系数随着蠕滑率的增大而急剧减小,此区域是打滑或空转区间,需要尽量避免列车进入此区域。在高速列车运行过程中,若能保持其蠕滑率始终在蠕滑区范围内,则可避免出现危害列车运行安全的空转或打滑现象。

图1 干燥和潮湿轨面条件下的黏着特性曲线
轮轨间黏着防滑约束条件可以表示为
|λ|<λopt
(10)
式中:λopt为最优蠕滑率,其定义为
λopt=argmax[μ(λ)]
(11)
在式(10)约束下,列车实际工作点可以严格限制在稳定可靠的蠕滑区内,实现牵引力或制动力的有效传递。因此,若能设计满足式(10)约束,同时实现蠕滑率λ对期望蠕滑率λ*精确跟踪的控制算法,则可以保证蠕滑率始终保持在蠕滑区域内,在防止车轮滑动的前提下,提供满足牵引力和制动力要求的黏着力。
由式(6)可知,蠕滑率存在奇点,并非一致连续可导,因此利用蠕滑率来表现蠕滑,可能导致控制算法中的盲点,影响控制效果[8],而蠕滑速度为
vs=ωr-v
(12)
结合式(6)可得
vs=max(ωr,v)λ
(13)
因此,可以选择蠕滑速度代替蠕滑率来表示蠕滑现象,设计控制算法,避免函数非一致连续可导问题。式(10)所示的黏着防滑约束条件等效为
|vs| (14) 由于轮轨之间复杂的黏着关系,精确的最优蠕滑率λopt难以获得,公式(14)不能直接应用于控制器设计。因此,将黏着防滑约束条件定义为 |vs| (15) 式中:λallow>0,为允许蠕滑率的上限,可以根据大量的实验或经验估计得到,其中 (16) 式中:v0>0,是由设计者选定的一个很小的常数。 至此,考虑牵引与制动转矩产生过程和黏着防滑约束的高速列车动力学模型可由式(1)、式(2)、式(7)以及式(15)来描述。同时,控制目标转化为设计控制策略使得在式(15)所示约束条件下,实现蠕滑速度vs对期望蠕滑速度vs*的精确跟踪。 δ=vsmax-|vs*|=vbλallow-|vs*|>0 (17) 高速列车的轮轨黏着力Fa和非线性运行阻力Fr难以参数化或测量得到,本文利用干扰观测器原理设计两个力观测器得到Fa和Fr的估计值分别为[12] (18) (19) 假设2:o(·)有界,其引入的扰动项不会对列车运行造成完全不可控的影响。 考虑式(15)约束下,式(1),式(2)和式(7)所表示的列车动态模型,借鉴反步控制逐层设计虚拟控制量的思路,引入一阶低通滤波器实现动态面控制,引入BLF处理输出约束问题,由此,本文提出高速列车蠕滑速度的动态面跟踪控制算法,设计步骤为: Step1定义实际蠕滑速度vs与期望蠕滑速度vs*之间的跟踪误差变量为evs,即 (20) 其误差动态方程为 (21) 选取对数型BLF函数 (22) 设系统的起始状态vs(0),满足evs(0)∈(-δ,δ)。对式(22)进行求导可得 (23) (24) 式中:k1为正实数;L1和L2为集总参数项,其中 (25) (26) (27) 式中:τd>0,为时间常数。 Step2定义eT=Tn-Tnd,对其求导,并结合式(9)可得 (28) (29) (30) 以上控制律设计中假设α,β均已知。若α,β未知,可以设计自适应律来估算其值。 (31) (32) (33) 式中:k2为正实数。 设计向量参数ea的自适应更新律为 (34) 式中:θ2为正实数。 定义滤波误差为 (35) 结合式(27),滤波误差的动态方程为 (36) (37) 证明:对V求导可得 (38) 由式(23)、式(24)、式(35)以及Young不等式可得 (39) 由式(32)~式(34)可得 (40) 应用不等式 (41) 进一步可得 (42) 由文献[17]可知,对于任何正实数δ,若|evs|<δ,则下列不等式成立 (43) 将式(37)、式(39)和式(42)代入式(38),并结合式(43),可得 (44) (45) (46) 进一步可得到 (47) (48) 需要说明的是,虽然在稳定性证明中涉及未知参数α,β,εd和η,但是控制算法并不需要用到这几个参数的实际值;常数k2的取值范围中虽然含有未知参数α和β,但只要k2取值足够大,可以满足算法要求。 需注意的是,当|vs|≥vsmax或|vs|≤vsmax-2δ时,|evs(0)|≥δ(0),不满足以上控制算法对于|evs(0)|<δ(0)的要求,此时系统的稳定性将变得不确定。 (49) 为了得到改进的统一全局控制算法,定义变量q (50) 结合式(24)、式(49)及式(50),设计虚拟控制量可写为 (51) 定理2对式(1)、式(2)、式(7)和式(15)所表示的高速列车动力学模型,采用全局防滑控制算法,设计动态面控制律为式(33),虚拟控制量为式(51),未知参数自适应更新律为式(34),双力观测器为式(18)和式(19),若假设1~假设3成立,初始条件满足对于任意正数p,有V0(0)≤p,则存在设计常数k1,k2,τd,θ2和常数矩阵Γ,使得闭环系统跟踪误差evs半全局一致最终有界,通过选取满足条件的合适设计参数,系统的稳态跟踪误差可以任意小,而且:(1)若|vs(0)| 证明:分3种情形进行证明。 (52) 对其求导,并结合式(21)、式(37)、式(42)、式(51)以及Young不等式可得 (53) (54) (55) 情形3:当|vs(0)|≥vsmax(0)时,同样构造式(52)所示的Lyapunov函数,参考情形2证明,易知evs是半全局一致最终有界的,只要设计参数合理,|evs|总能在有限时间T内进入|evs|<δ范围内,一旦进入|evs|<δ范围,控制器变为情形1。因此t>T后,蠕滑速度不会再超出设定上限,系统的跟踪误差evs可以任意小。 综合上述3种情况,在高速列车运行过程中,采用定理2所述黏着控制算法,系统的蠕滑速度跟踪误差evs半全局一致最终有界稳定,取适当的控制器参数,evs可以任意小。当|vs(0)| (56) 为了验证本文所提出建模与控制方法的有效性,应用MATLAB(R2013a)软件进行了计算机仿真验证。考虑列车车辆的1/4模型,具体实验对象参数见表1[9]。 表1 模型实验对象参数 为了模拟轨面突变情况下控制算法的有效性,采用干燥和潮湿两种不同轨面,黏着特性曲线如图1所示。具体设置情况见表2[9],表中轮轨黏着条件参数见式(5)。 表2 黏着特性曲线参数值 在高速列车的制动阶段(300 s以后),ω>0.1 rad/s时,取 本次仿真模拟高速列车在400 s时间内的运行过程,其中0~300 s为高速列车的牵引阶段,300 s以后为制动阶段。轨面状态变化分别发生在100 s(由潮湿轨面到干燥轨面)和330 s(由干燥轨面到潮湿轨面)。图2为高速列车运行过程中的车体速度和车轮速度曲线。图3和图4分别为高速列车的牵引与制动转矩Tn以及期望的牵引与制动转矩Tnd曲线。可以看出,列车经过200 s左右的牵引加速阶段,速度从0上升到大约69 m/s,然后接下来的100 s为高速列车的巡航阶段,300 s以后为列车的制动阶段,大约经过72 s列车速度下降到0。在整个控制过程中,即使是在两次轨面状况突变时,所设计的控制算法也能够及时适当的调整列车的牵引与制动转矩,使其很好的跟踪期望值,列车车体速度以及车轮速度均变化平滑,车轮没有出现滑动现象。 图2 列车车体和车轮速度曲线 图3 列车牵引与制动转矩曲线 图4 期望牵引与制动转矩曲线 图5 蠕滑速度轨迹曲线 图6 蠕滑速度局部轨迹曲线 图7 蠕滑率轨迹曲线 图8为高速列车蠕滑速度跟踪误差轨迹曲线。由图8(a)可以看出,即使是在轨面状态突变时,蠕滑速度跟踪误差evs也没有超出界限,始终被限制在(-δ,δ)之间。图8(b)为稳态误差局部放大图,可以看出稳态跟踪误差接近于0。 图8 蠕滑速度跟踪误差轨迹曲线 本文提出的算法实现了高速列车的主动黏着防滑控制,当高速列车的初始状态没有发生空转或打滑现象时,可以实现高速列车在运行过程中蠕滑速度始终不超过给定最大蠕滑速度上界,不会发生车轮滑动现象;当高速列车的初始状态发生空转或打滑现象时,系统会在有限时间内进入到蠕滑区,此后不会再发生车轮滑动现象。算法对期望蠕滑速度实现了较好跟踪,稳态跟踪误差可以任意小。该算法可以有效主动避免高速列车在运行过程中可能出现的空转和打滑现象,提高列车运行的安全与可靠性能。 本文建立了考虑牵引与制动转矩产生过程的高速列车动力学模型,将黏着防滑问题描述为含输出约束的非线性系统的跟踪控制问题,采用力观测器估计未知时变的黏着力和运行阻力,采用自适应律实现对未知参数的估算,引入BLF函数实现对蠕滑速度上界的限制,设计了高速列车蠕滑速度的动态面跟踪控制算法,实现了高速列车的全局主动黏着防滑控制。仿真结果表明,本文所提控制方法,能在对蠕滑速度进行上界约束的同时,产生满足牵引力和制动力要求的黏着力,蠕滑速度跟踪误差可以任意小,可保障黏着控制系统的稳定性。该算法同样可以应用于最佳蠕滑速度(或最佳蠕滑率)的精确跟踪,获取最大黏着力,实现列车的最优黏着防滑控制。2 蠕滑速度跟踪控制算法设计及稳定性分析
2.1 基本控制算法设计及稳定性分析






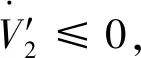











2.2 全局控制算法设计及稳定性分析
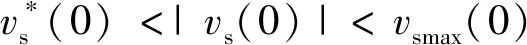




3 仿真结果与分析




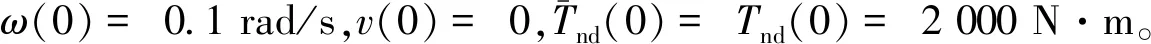



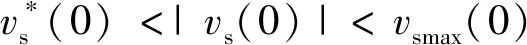




4 结束语

