基于板元分析法的梯形截面箱梁畸变效应研究

王兆南，张元海

(兰州交通大学 土木工程学院，甘肃 兰州 730070)

箱梁畸变一直是桥梁科研设计人员研究的一个热点，研究采用的解析方法有能量变分法、板元分析法、广义坐标法等。文献多采用能量变分法研究矩形和梯形截面箱梁的畸变效应，而板元分析法目前多用于分析矩形截面箱梁的畸变效应。郭金琼等[1]采用板元分析法研究了单箱单室矩形截面箱梁的畸变效应。马磊等[2]采用板元分析法推导了单箱双室波形钢腹板矩形截面箱梁的畸变控制微分方程。项海帆等[3]采用能量变分法对梯形截面单箱单室箱梁进行了畸变效应的研究。张元海等[4-5]提出了一种与薄壁箱梁约束扭转分析相似的箱梁畸变效应分析方法，并基于势能驻值原理导出了单箱单室箱梁的畸变控制微分方程。徐勋等[6-7]以广义坐标法为基础，对薄壁箱梁以畸变角和畸变挠度为位移参数的两种畸变理论进行比较分析，研究了箱梁的畸变效应。鲍永方等[8]对畸变计算理论和广义坐标法进行了分析对比。钱寅泉等[9]以畸变挠度为位移参数研究箱梁的畸变效应。对复杂的多室箱梁的畸变效应多借助于有限元进行研究，如采用考虑了畸变自由度的梁单元，实体单元或是考虑拉弯、扭转、畸变的空间分析单元对多室箱梁、薄壁曲箱梁的畸变等空间效应进行了精确的分析[10-18]。狄谨等[19]、刘保东等[20]对波纹钢腹板梁式桥的畸变性能进行了研究，并通过试验进行了验证。

以上文献，采用板元分析法对梯形截面箱梁的畸变进行研究的较少。本文以梯形截面单箱单室箱梁腹板和底板的夹角改变为未知量，采用板元分析法，以离散的箱梁各板元力系分析得出箱梁畸变控制微分方程。矩形截面箱梁一般采用坡度挠度公式推导横向板端弯矩和畸变角之间的关系[1-2]，梯形截面箱梁由于腹板倾斜，仍采用此公式推导过程将变得繁琐，但若用图乘法找出箱梁各板元横向板端弯矩和畸变角之间的关系，推导过程将变得简单。最后本文对得出的畸变控制微分方程进行了数值验证，研究了相关参数对箱梁畸变的影响。

1 箱梁各板元面内力系分析

在竖向偏心荷载作用下箱梁将发生畸变，本文以图1所示的梯形截面箱梁为研究对象。

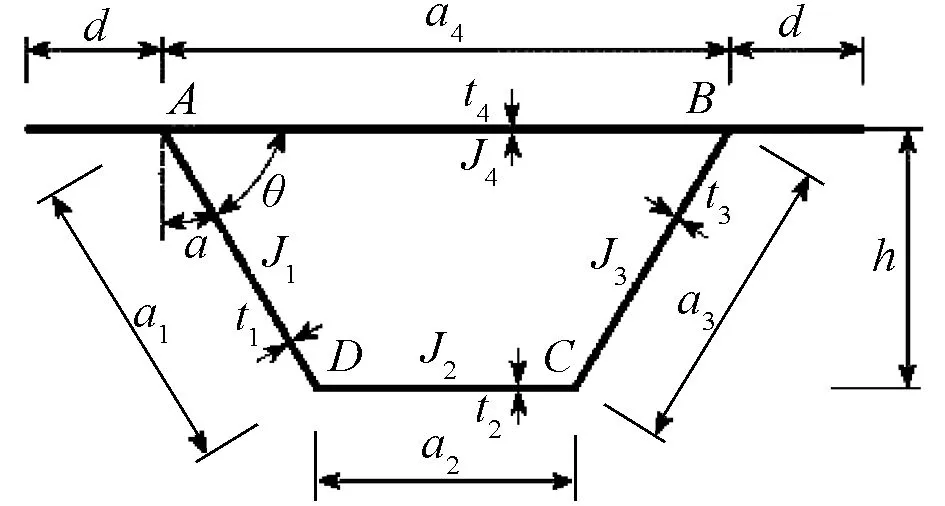
图1 梯形箱梁横截面

箱梁所受的偏心荷载可分解为正对称荷载和反对称荷载，反对称荷载P可分解为图2所示的畸变荷载Vd1、Vd2、Hd1、Hd2，分析采用的坐标系见图2。

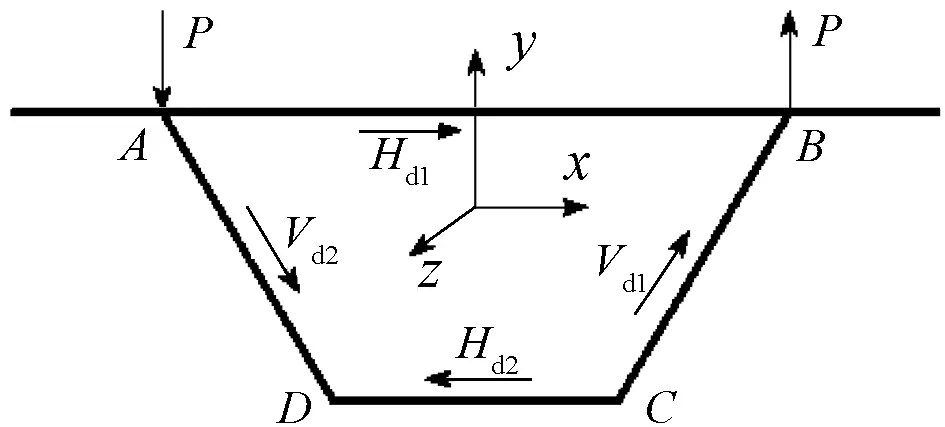
图2 箱梁畸变荷载

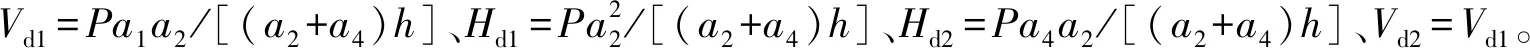
1.1 顶板、底板、腹板面内力系分析

取离散成板元的箱梁顶板为研究对象，分析顶板的面内力系，如图3(a)所示。qxB、qxA为箱梁腹板对顶板的横向约束反力，Todz为微段上腹板对顶板的纵向约束反力，Hd1为顶板面内畸变荷载，dQo、dMo为顶板微段上产生的面内剪力和力矩增量。对顶板列取面内力矩平衡方程，忽略式中的小量，化简后得

图3 顶板及底板面内力系

(1)

在顶板面内沿x轴列取平衡方程，可得顶板畸变荷载Hd1、腹板对顶板的横向约束反力qx1、顶板面内剪力增量dQo之间的关系为

dQo=Hd1-qx1

(2)

式中：qx1=qxA+qxB。

底板的面内力系如图3(b)所示，qxC、qxD为箱梁腹板对底板的横向约束反力，Tudz为微段上腹板对底板的纵向约束反力，Hd2为底板面内畸变荷载，dQu、dMu为底板微段上产生的面内剪力和力矩增量，同理可求得底板上面内力矩之间的关系为

(3)

在底板面内沿x轴列取平衡方程，可得底板畸变荷载Hd2、腹板对底板的横向约束反力qx2、底板面内剪力增量dQu之间的关系为

dQu=Hd2-qx2

(4)

式中：qx2=qxC+qxD。

如图4所示，取左腹板为分离体，qyA、qyD为箱梁顶板和底板对左腹板的横向约束反力，Todz、Tudz为微段上顶板和底板对腹板的纵向约束反力，Vd2为左腹板面内的畸变荷载，dQc、dMc为左腹板微段上产生的面内剪力和力矩增量。

图4 腹板面内力系

通过列取腹板面内力矩平衡方程，忽略式中的小量并化简后得

(5)

沿坐标y轴列取左腹板面内力系平衡方程，可得畸变荷载Vd2、左腹板面内剪力增量dQc、顶板和底板对左腹板的横向约束反力qyA、qyD之间的关系为

dQc=qy-Vd2

(6)

式中：qy=qyA+qyD。

将式(1)、式(3)代入式(5)并微分一次，然后代入式(2)、式(4)、式(6)后得

(7)

式(7)表征了箱梁各板元面内力矩、畸变荷载以及各板元之间相互约束的关系。

1.2 各板元面内力矩之间的关系

当截面发生畸变翘曲变形时，顶板、腹板、底板上由畸变翘曲应力合成的力矩为Mo、Mc、Mu，其方向如图5所示。

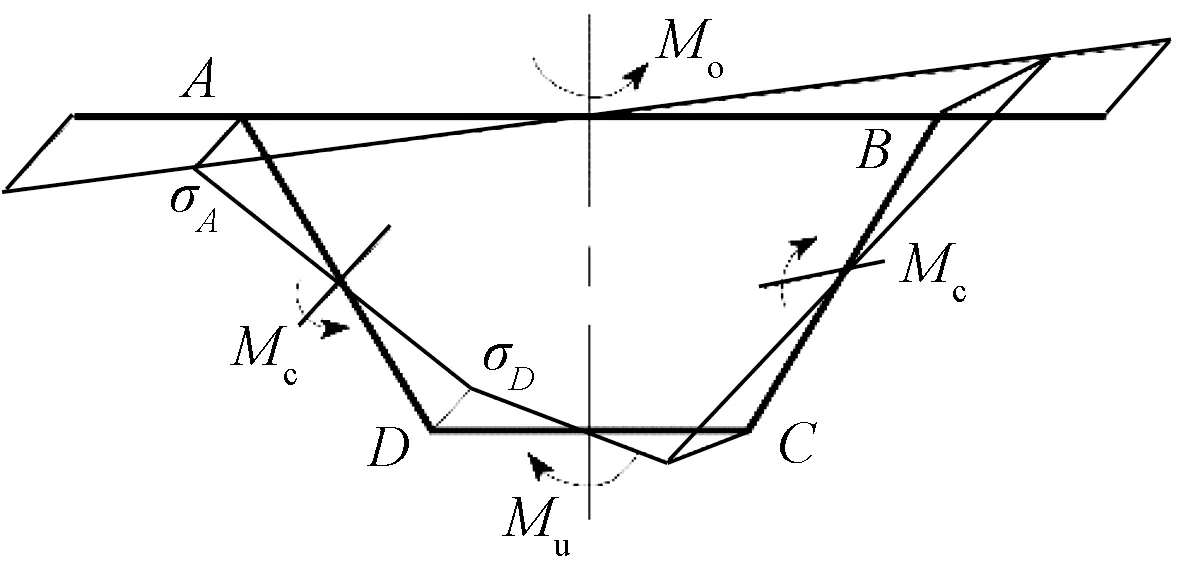
图5 畸变引起的各板元面内力矩

以σA和σD分别表示角点A和D的畸变翘曲正应力，设β=σD/σA，可得顶板、底板和腹板面内力矩二次微分之间的关系为

(8)

将式(8)代入式(7)得到关于腹板面内力矩和各板元上力系之间的平衡微分方程，即

(9)

1.3 腹板面内力矩和畸变角的关系

定义图6中箱梁框架D点的夹角改变为畸变角γ。箱梁上作用有畸变荷载时，沿梁z轴向取出单位长度的梁段形成的框架，当产生畸变角为γ的畸变变形时，如图7所示，则各板端的位移为uA、uD、vA、vC。根据箱梁畸变协调原理[1]，箱梁框架的畸变角γ可采用图7中各板端位移来表示，即

(10)

对式(10)微分两次，考虑梁的挠曲和力矩之间的关系以及式(8)，可得畸变角γ和腹板面内力矩Mc的关系为

图6 箱梁畸变角

图7 畸变横向框架变形

γ″=Γ2Mc

(11)

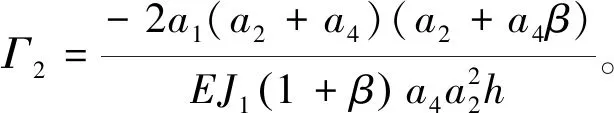
将式(11)微分两次，则有

(12)

将式(12)代入式(9)，得到关于畸变角γ和板元上力系之间的平衡微分方程

(13)

式中：EIωd为箱梁的抗畸变翘曲刚度(Iωd的单位为m6)。

2 箱梁各板元面外力系分析

将图7中框架各板元离散成分离体，各板元上的面外力系如图8所示。其中mAB、mBA、mCD、mDC、mAD、mDA、mBC和mCB分别为框架顶板、底板、腹板的面外板端弯矩，qyB、qyC为框架顶板和底板对右腹板的横向约束反力。分析各板元上面外力系的平衡，可得各板元面外力系之间的关系。

图8 箱梁各板元面外力系

2.1 顶板、底板、腹板面外力系分析

对箱梁框架顶板和底板分别列取关于面外力系的平衡方程，得出

(14)

则左腹板上由顶板和底板的约束反力合成的作用力qy为

(15)

腹板在面外力系的作用下，根据力矩平衡可以得出

(16)

则箱梁框架顶板上由于腹板约束反力合成的水平作用力qx1为

(17)

同理得出底板上的水平作用力qx2为

(18)

将式(15)、式(17)、式(18)代入式(13)中的qy+a1qx1/(2a4)+a1qx2/(2a2)后，该部分变为

(19)

2.2 各板元横向板端弯矩和畸变角的关系

采用坡度挠度公式推导矩形截面箱梁横向板端弯矩和畸变角之间的关系较为方便，但梯形截面箱梁因腹板倾斜，采用此公式时，推导过程将变得复杂。本文采用图乘法来导出畸变角γ和各板元横向板端弯矩之间的关系，进而求得箱梁横向框架刚度，过程较为简单。

箱梁发生图6所示的水平侧移和发生图7所示的畸变角为γ的畸变变形具有的应变能相等[3]，角点D的夹角改变量为γ时，顶板的水平位移为γa1sinθ。当箱梁顶板B点作用单位水平力时顶板的侧移值为δh，顶板跨中剪力值为X，δh和X可采用图乘法求出。当顶板B点的水平位移为γa1sinθ时，顶板B点作用的水平力为γa1sinθ/δh，有a1sinθ=h，则顶板跨中剪力值为γhX/δh，对A点取矩有mAB=γa4hX/(2δh)=mAD，亦可得mDC=γ(2h2-a2hX)/(2δh)=mDA。令k1=a4hX/(2δh)，k2=(2h2-a2hX)/(2δh)，则mAB=mAD=k1γ，mDC=mDA=k2γ，将其代入式(19)有

(20)

并令

(21)

式中：

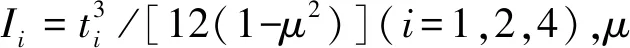
在a1Hd1/(2a4)+a1Hd2/(2a2)+Vd2中代入畸变荷载表达式，并令Ω=a1(a2+a4)/(2h)，可得

(22)

3 畸变控制微分方程及其解

通过以上分析，最后得到以角点D的畸变角γ为未知量的梯形截面箱梁四阶畸变控制微分方程

EIωdγ″″+EIRγ=PΩ

(23)

求解方程式(23)可以得到待求截面的畸变角γ，畸变双力矩Bdω，根据相关关系可以求得箱梁截面上的畸变翘曲正应力。令IR/Iωd=4λ4，则λ=[IR/(4Iωd)]1/4，方程式(23)变换为

γ″″+4λ4γ=PΩ/(EIωd)

(24)

根据箱梁畸变微分方程和弹性地基梁挠曲微分方程的相似关系，可得箱梁跨中作用一单位畸变荷载时，箱梁畸变角和畸变双力矩的影响线[1-3]。当箱梁跨中作用一单位畸变荷载时，畸变微分方程的初参数解分为两种情况：

(1)设梁长为L，若λL>2π，则解为

(25)

(2)若λL≤2π，则解为

(26)

式中：z为箱梁各截面距跨中坐标原点的距离；γ0、Bdω0、Qdω0分别为坐标原点的畸变角、畸变双力矩及畸变矩，其值可由相应的边界条件确定[4-5]。

4 数值算例及参数分析

4.1 数值算例

算例1 简支单箱单室矩形截面箱梁的计算跨径L=39.6 m，材料弹性模量E=35 GPa，截面尺寸a1=a3=3.1 m、a2=a4=2.6 m、d=0.4 m、t1=t3=0.207 m、t2=0.217 m、t4=0.259 m。令PΩ=1 kN·m作用在梁跨中，坐标原点在跨中并沿梁长将梁等分成10段共计11个截面，取一半梁长的计算结果，有限元计算采用板单元，通过计算各截面的畸变角和畸变双力矩验证本文推导公式的正确性。将本文解、文献[1]解及有限元解列出，如表1和表2所示，在0.3L截面处，本文得出的畸变角和文献[1]的误差为8.99%，和有限元解的误差为3.24%，其余截面数值相互吻合较好；畸变双力矩本文解和文献[1]解吻合较好。

表1 算例1畸变角

注：误差①=(本文解-文献解)/文献解×100%，误差②=(本文解-有限元解)/有限元解×100%，以下同。

表2 算例1畸变双力矩

算例2 简支单箱单室矩形截面箱梁的计算跨径L=80 m，材料弹性模量E=35 GPa，截面尺寸a1=a3=3.0 m、a2=a4=5.0 m、h=3.0 m、d=1.5 m，各板件厚度均为0.2 m。分析过程同算例1，单位畸变荷载作用下的畸变角和畸变双力矩计算结果如表3和表4，在0.3L截面处，本文得出的畸变角和文献[3]的误差为12.58%，和有限元解的误差为4.74%，其余截面数值相互吻合较好；畸变双力矩在0.2L截面处，本文解和文献[3]误差偏大，但误差不超过10%，其余截面数值吻合良好。

表3 算例2畸变角

表4 算例2畸变双力矩

将文献[1]、文献[3]和本文对算例中畸变相关参数的计算值列于表5，可以看出本文计算的参数值和文献给出的值吻合较好。

表5 畸变参数比较

注：括号内数据为文献值。

算例3 梯形截面单箱单室简支梁桥的计算跨径L=40 m，材料弹性模量E=35 GPa，截面尺寸a1=a3=2.47 m、a2=4.45 m、a4=6.25 m、h=2.3 m、d=1.5 m、t1=t3=0.35 m、t2=0.27 m、t4=0.25 m。荷载和分析过程同算例1，计算结果见表6，除了在箱梁0.3L截面处畸变角误差偏大，其余截面本文解和有限元解吻合较好。

表6 算例3畸变角

4.2 梁高和腹板倾角变化对箱梁畸变的影响

单箱单室简支梁桥的计算跨径L=40 m、材料弹性模量E=35 GPa，截面尺寸a1=a3=2.3 m、a2=a4=6.25 m、d=1.5 m、t1=t3=0.35 m、t2=0.27 m、t4=0.25 m，以此截面尺寸为基础研究梁高h和腹板倾角α变化对箱梁畸变的影响。单位畸变荷载作用在箱梁跨中，分析过程同算例1，采用本文解析公式计算。首先，改变梁高，以梁高h=2.3 m为初始值，0.3 m为增量，增加到h=3.8 m，截面其他尺寸保持不变；其次，通过改变底板宽度以达到腹板倾角变化的目的，底板宽度以6.25 m为初始值，变化量为0.6 m，变到宽度为3.25 m，梁高及其他截面尺寸不变，由于数据较多，取具有代表性的数值予以分析。

(1) 梁高h变化对箱梁畸变的影响

如图9所示，畸变角大小沿梁长方向分布不一致，在跨中截面有最大值，在0.3L截面附近由正值变为负值，在0.4L截面处有最小值。当梁高h逐渐增大时畸变角在跨中截面、0.4L截面处逐渐减小，在0.3L截面附近变化较小。如图10所示，畸变双力矩沿梁长方向在跨中截面有最大值，在0.1L～ 0.3L截面范围内由正值逐渐变为负值。当梁高h逐渐增大时，畸变双力矩值在跨中截面增长较快，并随梁高h的增大其值逐渐增大。

梁高h变化时，畸变角和畸变双力矩值变化趋势不同，在跨中截面，畸变角随梁高增大其值逐渐变小，畸变双力矩则逐渐增大；畸变角在0.3L截面附近逐渐减小为0，畸变双力矩在0.1L截面附近逐渐减小为0；畸变角在0.4L截面处有最小值，其绝对值随梁高h增大逐渐增大，畸变双力矩在0.2L～ 0.3L截面范围内有最小值。

图9 梁高h变化时畸变角沿梁长的变化

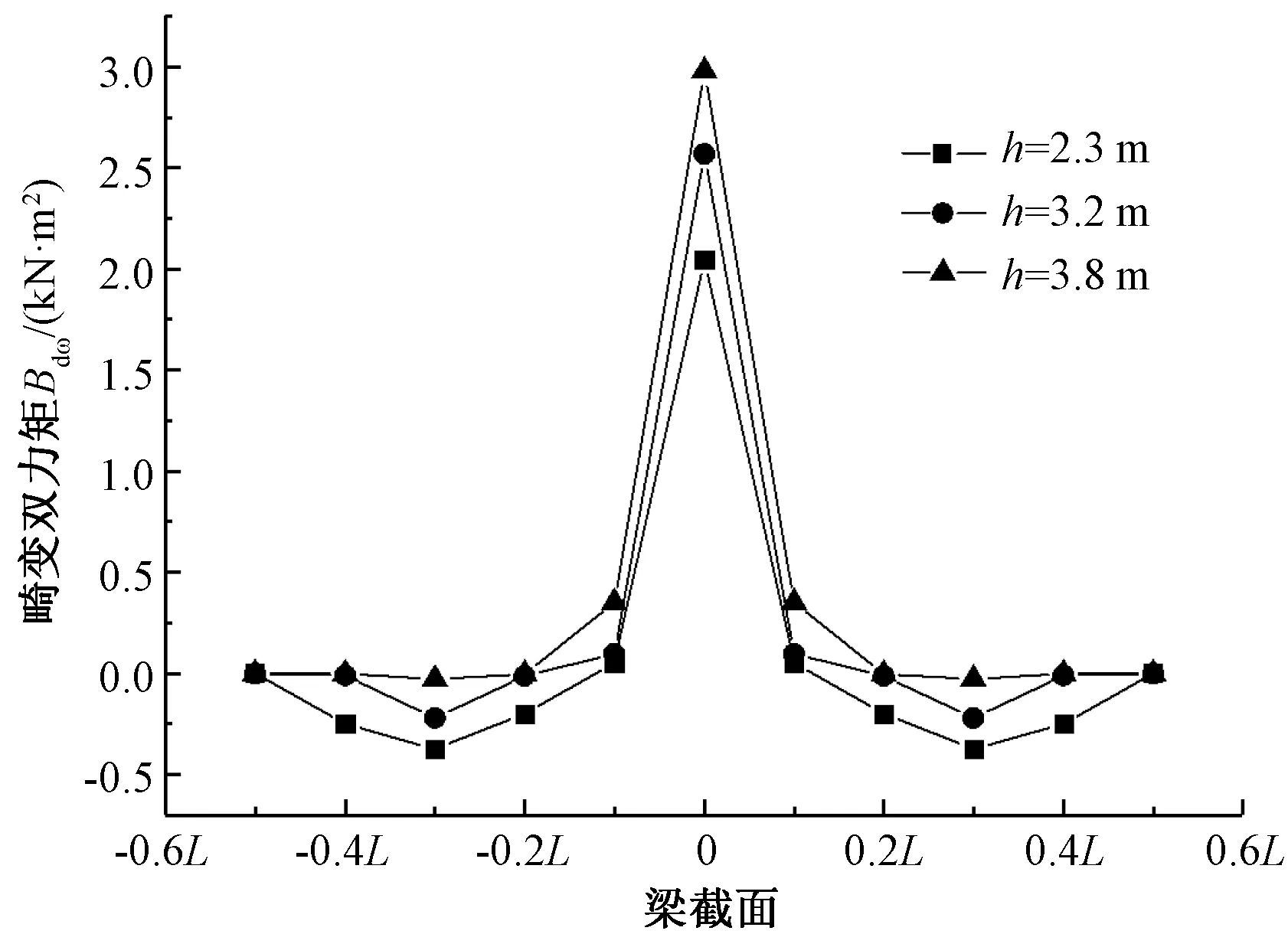
图10 梁高h变化时畸变双力矩沿梁长的变化

(2) 腹板倾角α变化对箱梁畸变的影响

腹板倾角α变化时畸变角和畸变双力矩沿梁长的分布同梁高h变化时的分布类似。当腹板倾角逐渐增大时，畸变角在跨中截面先增大后减小，从本文的分析得出，腹板倾角为21.37°即底板长度为顶板长度的0.7倍时，跨中截面畸变角有最大值，畸变角在0.3L截面附近变化较小，如图11所示。随着腹板倾角逐渐增大，跨中截面畸变双力矩值逐渐减小，在0.1L截面附近畸变双力矩逐渐趋向于0，如图12所示。腹板倾角α变化时，畸变角和畸变双力矩值变化趋势不同，当腹板倾角逐渐增大时，跨中截面畸变角先增大后减小，畸变双力矩则逐渐减小；在0.3L截面附近畸变角变化较小，在0.1L截面附近畸变双力矩变化较小，在0.4L截面处畸变角有最小值，畸变双力矩在0.2L～ 0.3L截面范围内有最小值。

图11 腹板倾角α变化时畸变角沿梁长的变化

图12 腹板倾角α变化时畸变双力矩沿梁长的变化

5 结论

(1) 采用板元分析法推导出了单箱单室梯形截面箱梁以畸变角为未知量的四阶畸变控制微分方程，本文推导出的解析公式计算结果和相关文献的算例值、有限元解吻合良好，验证了公式的正确性。

(2) 采用图乘法导出箱梁各板元横向板端弯矩与箱梁畸变角之间的关系时，其过程比采用坡度挠度公式简单。

(3) 通过梁高变化对简支箱梁畸变效应的影响分析得出，箱梁跨中截面畸变角随着梁高增大逐渐减小，畸变双力矩随着梁高增大逐渐增大；畸变角在0.4L截面处有最小值，畸变双力矩在0.2L～ 0.3L截面范围内有最小值。

(4) 腹板倾角逐渐增大时，箱梁跨中截面畸变角先增大后减小，畸变双力矩则逐渐减小；在0.4L截面处畸变角有最小值，在0.2L～ 0.3L截面范围内畸变双力矩有最小值。