基于IMU标定补偿的列车组合定位优化方法

上官伟，谢朝曦，姜 维

(1.北京交通大学 电子信息工程学院，北京 100044；2.北京交通大学 轨道交通控制与安全国家重点实验室，北京 100044；3.北京市电磁兼容与卫星导航工程技术研究中心，北京 100044)

随着铁路运输的发展，为了保障列车运行安全、提高运输效率，对列车定位技术提出了更大的挑战。近年来，利用全球卫星导航系统(Global Navigation Satellite System，GNSS)和惯性导航系统(Inertial Navigation System,INS)构成组合导航系统已经成为列车定位的基本方式，利用两者优劣势互补的特点，使得定位结果的精度、可靠性和实时性较单一系统而言有极大的改善，是我国未来定位技术的主要发展方向之一。

由于传统的惯导系统价格昂贵、体积笨重，极大地限制了它在铁路领域的应用。近年来，微机械惯性测量单元(Micro Electro Mechanical Systems Inertial Measurement Unit,MEMS-IMU)具有低成本、小型化、抗强冲击的优势[1]，成为了组合导航领域最常见的惯性器件，其他领域包括航空、航海均开始了MEMS-IMU的应用推广[2-3]。但MEMS-IMU的测量精度普遍较低，当列车经过隧道、山谷、林区等卫星信号失锁区域，组合导航系统就仅依赖于惯导自身递推，而惯导系统的累积误差会随时间迅速增大发散，最终导致定位系统失效。为了弥补GNSS/INS组合导航的缺陷，国内外学者提出了许多方案。文献[4]在组合方式上采用鲁棒滤波方法增强数据融合算法，配合小波变换方法进行系统故障检测，保证系统可靠安全。文献[5]针对复杂列车定位环境，结合基于矢量跟踪的深耦合算法，提出了新型非线性滤波算法STCKF来增强定位性能的鲁棒性。文献[6]将多普勒频移引入GPS卫星接收机，利用基于LSKF算法的列车定位方法，提高卫星信号捕获。文献[7]采用多传感器融合的方法，在卫星导航和惯性导航的基础上增加了轮速传感器，并配合地图匹配的方式提高了卫星失效时的定位精度。从各类文献中可以总结出对组合导航改进方案的整体思想，主要分为三个方面：一是通过改进GNSS和惯导系统的耦合算法来提高鲁棒性；二是提高卫星接收机的信号捕获能力；三是增加传感器冗余。上述方式虽然能提高组合导航系统的定位精度和连续性，但没有从根源上减少惯性器件自身的误差，面对隧道等卫星信号完全失效环境仍存在定位困难。因而研究如何降低MEMS惯导系统的误差，使其在GNSS信号失效环境下也能满足定位需求具有积极的意义。

为此本文将结合列车运行环境和实际需求，针对安装误差、标度因数和零偏误差研究MEMS-IMU误差模型，提出加速度计和陀螺仪的误差参数标定方法，通过对其补偿从根源上降低惯性导航系统的累计误差，提高组合定位系统的精确性、连续性和有效性。

1 MEMS-IMU的误差数学模型

MEMS-IMU包含加速度计和陀螺仪，它们采集数据时受到多种因素影响产生误差项，按其来源通常可以分为两类[8]：一是惯性传感器的器件误差，主要包括零偏误差、刻度因子、启动漂移、温度漂移、非敏感轴互耦等；二是MEMS惯性传感器组合成惯性测量单元所产生的误差，主要是安装误差和杠臂效应。从理论上来说，考虑的误差项越多，对误差的描述越准确，最终补偿的效果精度会更高。然而，由于某些误差项本身对导航精度影响非常小，对其辨识却需要付出较高的代价[9]。由于MEMS器件内部采用微纳米级尺度加工成的微机械元件，受到结构加工与电路工艺的限制，对其精度影响较大的因素具体表现为安装误差、零偏误差、刻度因数[10]。因此本文考虑工程应用中的实际情况，针对零偏误差、刻度因数、安装误差这三项主要误差项建模并补偿。

1.1 陀螺仪误差模型

陀螺仪测量的是载体运动旋转角速度的传感器，MEMS陀螺仪关于上述三个误差项可建模为[11]

ωM=(I+ΔSω)MωωT+bω+εω

(1)

式中：ωM=[ωMxωMyωMz]T为陀螺仪的3个轴向的量测值；ΔSω=diag(ΔSωxΔSωyΔSωz)为陀螺仪3个轴向的刻度因数误差；Mω为陀螺仪的安装误差，包括器件非正交误差以及敏感轴与坐标轴之间的非对齐误差，为3×3矩阵；ωT=[ωTxωTyωTz]T为陀螺仪3个轴与相对应量测值的真值；bω=[bωxbωybωz]T为陀螺仪3个轴的零偏误差；εω=[εωxεωyεωz]T为陀螺仪3个轴的测量噪声，通常为零均值高斯白噪声。

令Aω=(I+ΔSω)Mω，Bω=bω，由于εω可以通过取均值的方式消除，因此MEMS陀螺仪的补偿模型可表示为

ωM=AωωT+Bω

(2)

1.2 加速度计误差模型

同样地，加速度计与陀螺仪具有类似的外部误差形式[11]，为

aM=(I+ΔSa)MaaT+ba+εa

(3)

式中：aM=[aMxaMyaMz]T为加速度计3个轴的量测值；ΔSa=diag(ΔSaxΔSayΔSaz)为加速度计3个轴向的刻度因数误差；Ma为加速度计的安装误差，包括器件非正交误差以及敏感轴与坐标轴之间的非对齐误差，为3×3矩阵；aT=[aTxaTyaTz]T为三轴加速度计相对应量测值的真值；ba=[baxbaybaz]T为三轴加速度计的零偏误差；εa=[εaxεayεaz]T为三轴加速度计的测量噪声，通常为零均值高斯白噪声。

令Aa=(I+ΔSa)Ma，Ba=ba，εa可以利用求均值的方法消除，则式(3)可写为

aM=AaaT+Ba

(4)

2 MEMS-IMU标定方法

MEMS惯性器件的误差数学模型中，需要标定各项系数，如式(2)、式(4)中的A、B矩阵，进而对各种误差进行补偿。由于惯性器件对干扰的敏感性强，各项系数波动较大，因此若要得到高精度的标定结果，需要设计严密的实验和外部基准[12]。本文借助转台利用分立标定的方法对MEMS-IMU标定，该方案利用事先建立好的输入输出数学模型，以转台提供的高精度的方位基准和速率作为输入，与惯性器件的输出利用最小二乘法标定出各项参数，此方法简单、高效，能有效提高惯导系统精度。

2.1 坐标系的定义

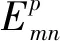
2.2 陀螺仪标定方法

首先计算MEMS陀螺的误差系数矩阵Aω、Bω，对此需要有一定的角速率输入才能激发误差项[14]。由于地球自转的角速度已知，因此传统高精度陀螺仪直接将地球自转作为激励，但由于MEMS惯性器件的测量精度较低，无法有效利用地球自转速度，因此需要转台提供适当的精确角速率。但转台的转动输出的参考系是地球坐标系(e系)，而惯性器件输出的参考系是地心惯性坐标系(i系)，为了保证惯性器件输入输出的一致性，惯性器件输入包含两部分：一是转台相对于地球的角速度，二是地球相对惯性空间的角速度。它等于为这两部分的矢量和，表达式为

(5)

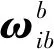
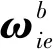
(1)计算矩阵Aω，令X轴朝天可以求得矩阵Aω的第一列系数，同理当Y、Z轴朝天时，利用相同的步骤可得矩阵Aω的第二、三列元素值，进而求得整个矩阵值。

以X轴为例，当X轴朝天并且转台绕X轴以角速率ω旋转时，设采样间隔为t，则陀螺的输入角速率可以表示为

(6)

式中：L为当地纬度；ωie为地球自转角速率。

将式(6)代入式(2),则得到输出表达式为

(7)

(8)

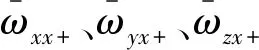
经过n个不同速率的采样值之后，代入式(8)第1个分式，写成矩阵形式得到

Z=Hx+v

(9)

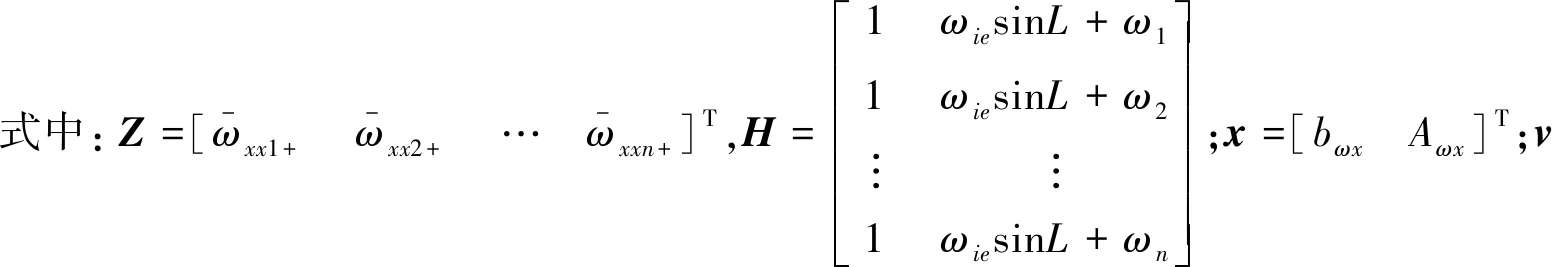
(10)

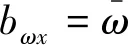
(11)

联立方程组式(8)、式(11)可以得到陀螺仪的三轴零偏误差为

(12)

至此，陀螺仪的误差参数全部标定完毕。

综上所述，利用上述原理标定陀螺仪参数的具体步骤可以归纳为：

Step1将转台和MEMS惯性器件连接完毕，接通电源并预热10 min。

Step2等待惯性器件输出稳定之后，绕某一轴以事先给定的角速度正向转动，转台至少转动3圈并记录陀螺输出值；将转台以同样的速率反向转动，转动时间与正向速率转动时间相同，并记录陀螺输出值。

Step3在采样数据中，提取转台转动整数周的陀螺输出值并将其取平均，得到一组输入输出的数据。

Step4转台依次以多组不同的角速度转动，重复Step2、Step3，得到多组不同的输入输出数据。

Step5利用式(10)、式(12)分别得到Aω矩阵和零偏误差的值。

2.3 加速度计标定方法

加速度计的标定是通过静态多位置标定方法实现的，利用转台使得加速度计的3个轴分别敏感重力加速度，然后采集数据计算误差系数。加速度计模型包含误差参数的个数越多，需要转动的位置也就越多，本实验选择12位置标定方法，其编排位置如表1所示。

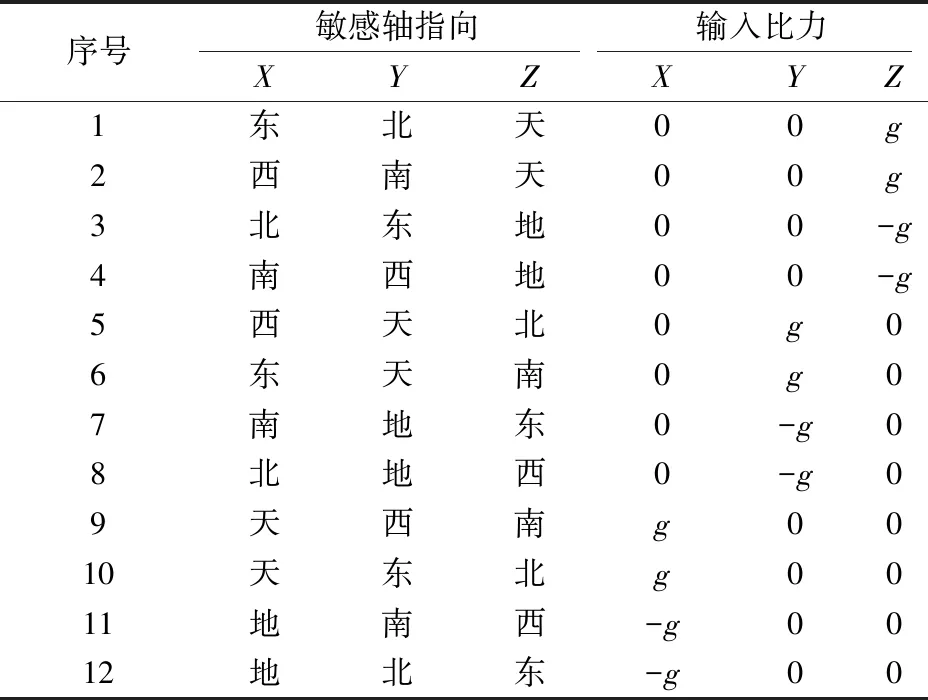
表1 加速度计标定编排方式

根据式(4)可以得到

(13)

对两边求转置得到

(14)

经过12次测量可获得12组式子，将其写成矩阵分量形式为

(15)

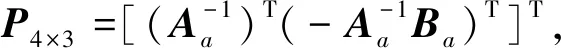
T12×3=M12×4·P4×3

(16)

利用最小二乘法得到加速度计的误差补偿系数矩阵为

P4×3=(MTM)-1MTT

(17)

结合上述原理，标定加速度计模型参数的具体步骤可以归纳为：

Step1将转台和MEMS惯性器件连接完毕，接通电源并预热10 min。

Step2依据加速度计标定的位置编排，以表1序号1为例，将转台转至水平位置，并使加速度计Z轴朝地，X轴朝东，Y轴朝西，等待惯性器件输出稳定之后，记录3 min的加速度计输出值，完成位置1的数据提取。

Step3转动转台至表1所示其余位置，得到其余的11组数据提取。

Step4将得到的12组数据代入式(17)可得加速度计整体的补偿矩阵P。

3 实验设备及数据分析

3.1 实验设备及环境

为了验证本文采用的惯性器件误差模型和标定方案，选取2018年7月京沈高速铁路实际行车数据进行试验，分为静态试验和动态试验，惯性测量单元使用ADIS 16488，内置在车载设备里，采集频率为123 Hz，见图1。

图1 试验设备及环境

3.2 静态试验结果

静态试验包括静止状态下IMU的输出值对比和定位结果的漂移分析。前者能验证误差模型和标定效果的好坏，后者可以检验IMU的改进对惯导系统定位精度的影响。静态试验数据选取列车停靠在新民站站内，停靠时间约2.5 min。

利用第2、3节所述的误差模型和标定处理方法对IMU进行补偿。结果见图2、图3，可以看出加速度计补偿前的X、Y、Z轴测量值有较大偏差，通过补偿校正之后，三轴测量结果得到明显的改善，均已回到真实值附近。同样，补偿之后陀螺仪X、Y、Z轴的输出测量值与理想输出较为吻合。

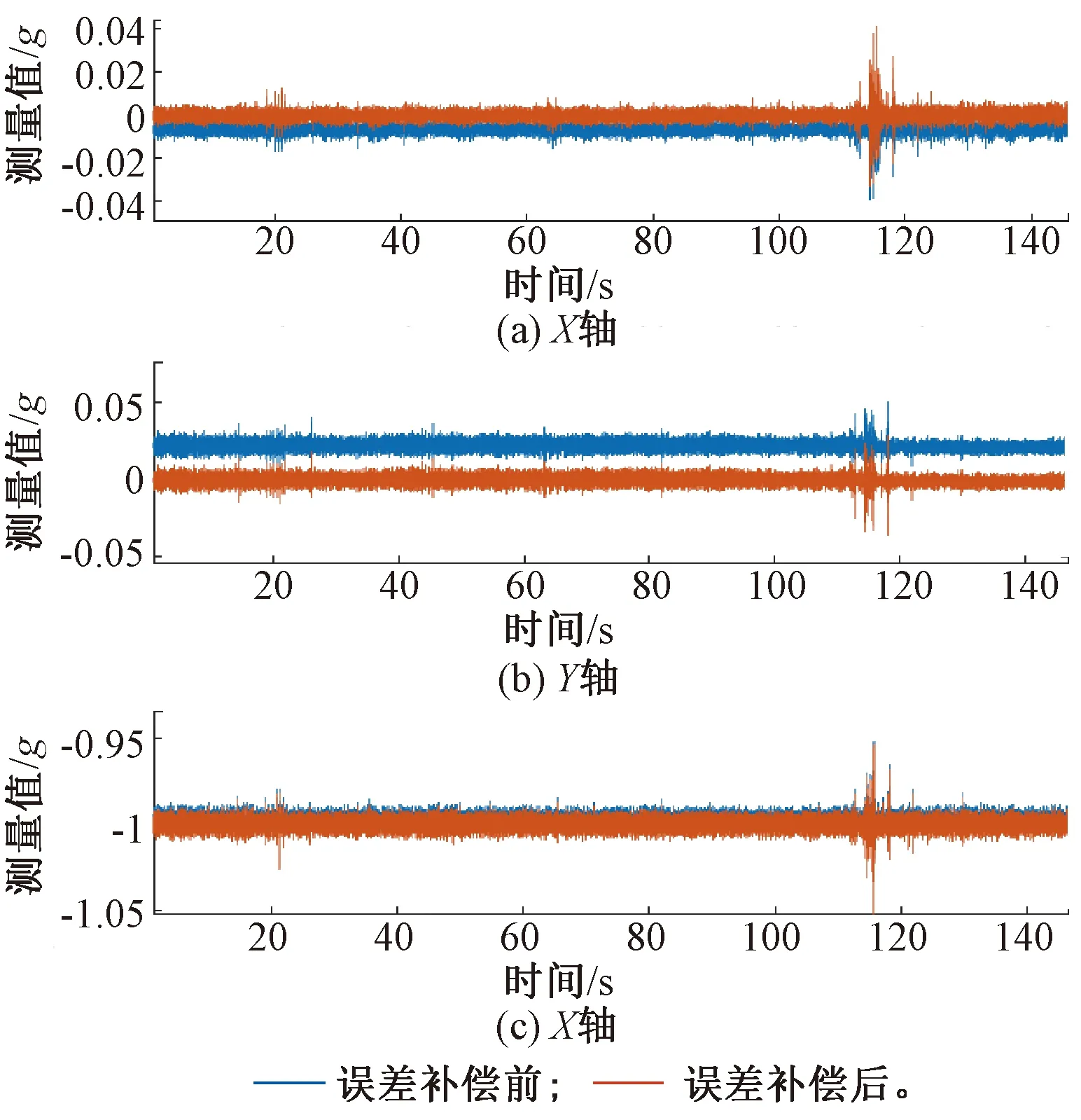
图2 补偿前后加速度计量测值对比

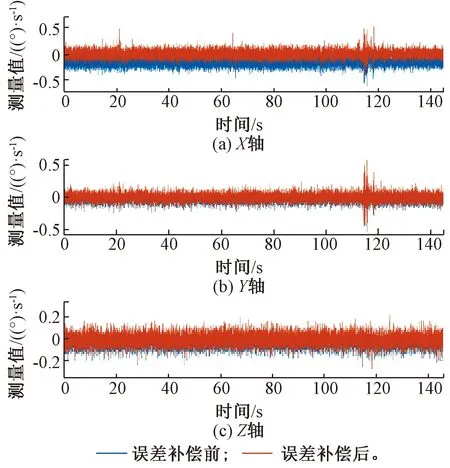
图3 补偿前后陀螺仪量测值对比

为了量化补偿前后的改进程度，表2、表3细致列出了补偿前后加速度计、陀螺仪各个轴测量的误差均值和均方根误差，可以看出，标定补偿之后，MEMS-IMU的误差均值至少提高了80%，说明误差的标定补偿能有效地消除惯性器件的确定性误差。

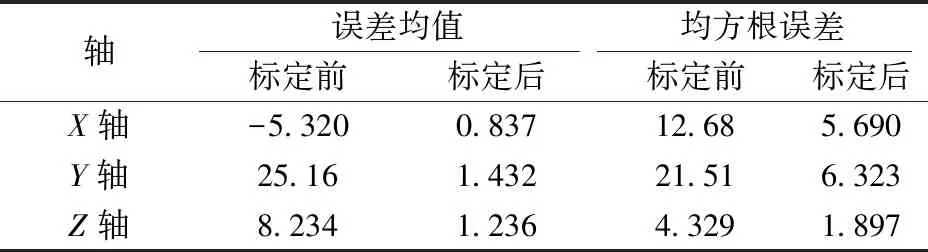
表2 加速度计标定前后量测误差对比 10-3g

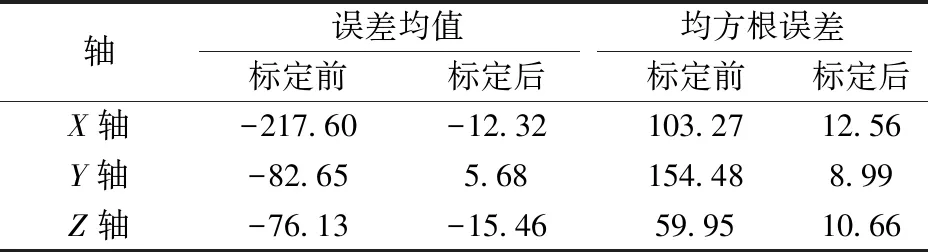
表3 陀螺仪标定前后测量误差对比 (°)/h

同时为了反映IMU的改进程度对列车运行定位的影响大小，利用补偿前后的IMU数据进行回放仿真。静止状态初始航向角为40.2°，速度为0，位置不变。考虑到列车的运行特性，主要对补偿前后的航向角、速度和位置误差进行对比分析，仿真结果见图4～图6。

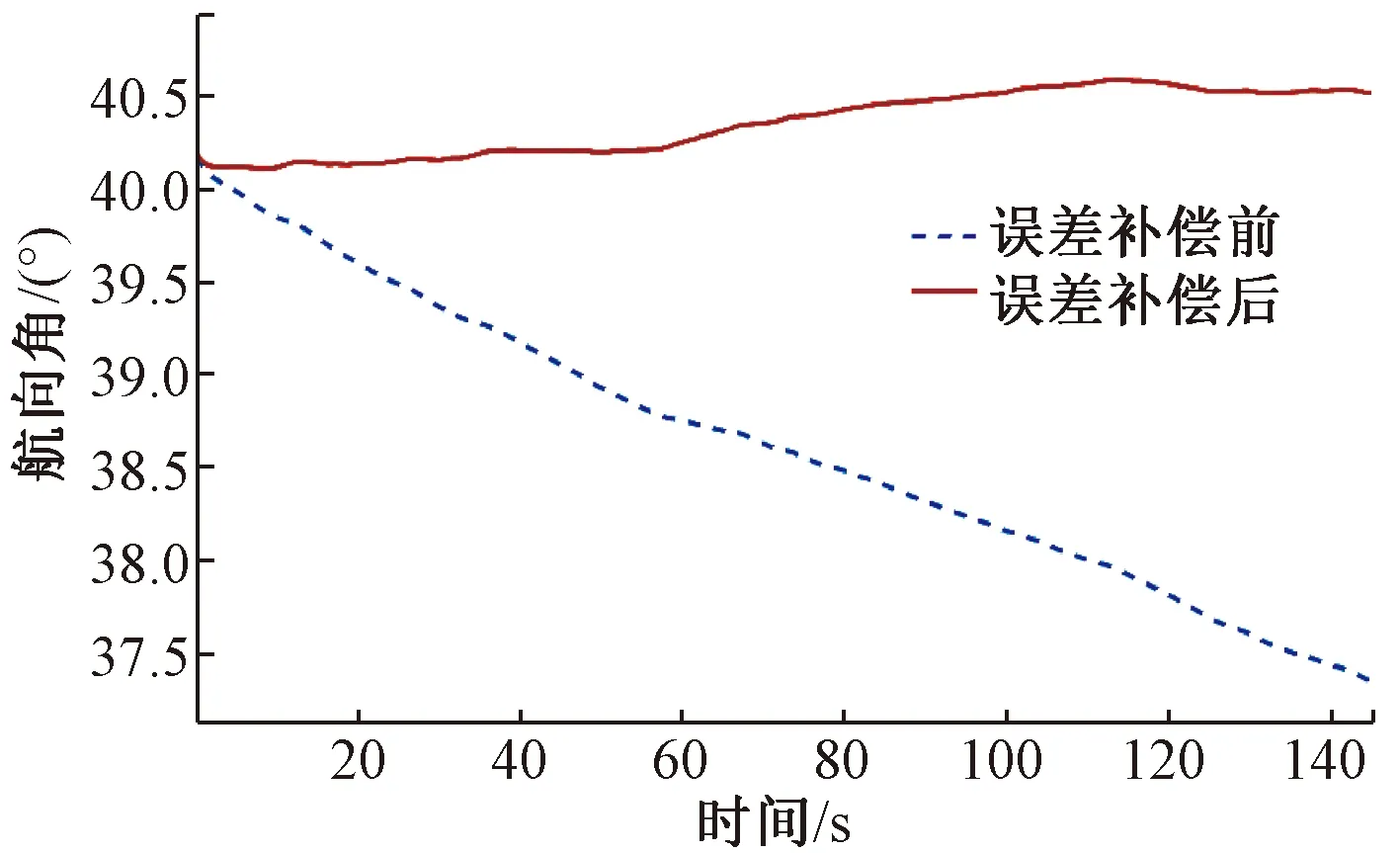
图4 静态航向角对比

图4通过比较陀螺补偿前后的航向角漂移，可以看出，误差补偿之前列车的航向角误差随时间增大而增大，经过140 s的运行最大误差达到3°。而误差补偿之后的航向角漂移较小，最大误差仅为0.4°，可以看出，陀螺补偿使静态姿态角精度提高86.67%。

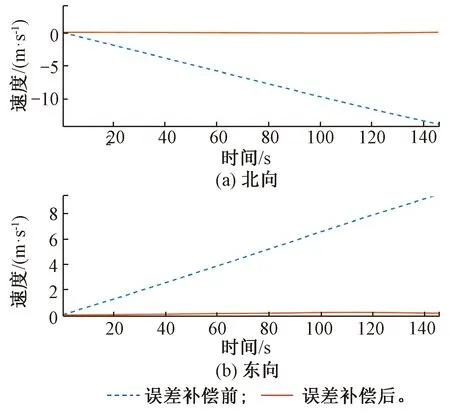
图5 静态速度对比

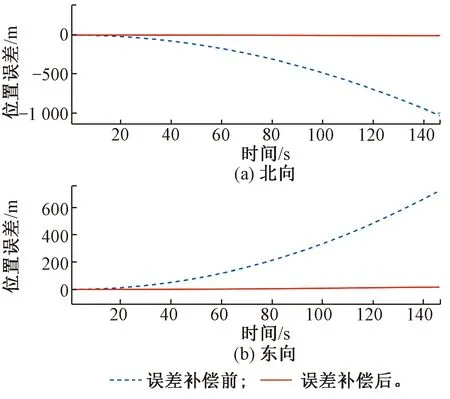
图6 静态位置误差

由图5可以看出，经过140 s的仿真时间，原始的IMU数据递推使得北向速度误差达到-13.26 m/s，东向速度误差达到9.202 m/s，速度漂移误差较大，并且随时间有递增趋势；而经过误差补偿之后，北向、东向速度误差分别为-0.016 85 m/s、0.149 1 m/s，说明加速度计的误差补偿极大地抑制了速度漂移。航向角和速度的改善直接影响最终定位精度，通过图6看到，整个运行过程惯性导航定位误差从百米数量级降低到10 m之内，极大地提高了定位精度。

综上所述，惯性器件的误差模型与标定方法有效且可行，通过标定补偿之后能有效降低静态定位误差。

3.3 动态试验结果

除了列车静态分析之外，还需验证列车处于运动状态补偿前后的各项参数的改进程度。动态试验路线位于阜新站到北票站之间，如图7红框区域，路线长约20 km，轨道航向变化范围在 -117°～-98°之间，为验证惯导系统导航解算和为IMU输出补偿提供有利的实验环境。当列车运行至该区域内，人为断开卫星信号，车载单元仅依靠惯性导航系统解算，列车在该段区域速度约为180 km/h，运行时间为7 min左右。

图7 现场实验线路

同时，列车上搭载战术级性能的IMU，与NovAtel的接收机组合为高精度SPAN (Synchronized Position Attitude &Navigation)系统，列车运行过程中位置、速度信息以它的输出作为参考,在GNSS信号失锁情况的误差如表4所示。

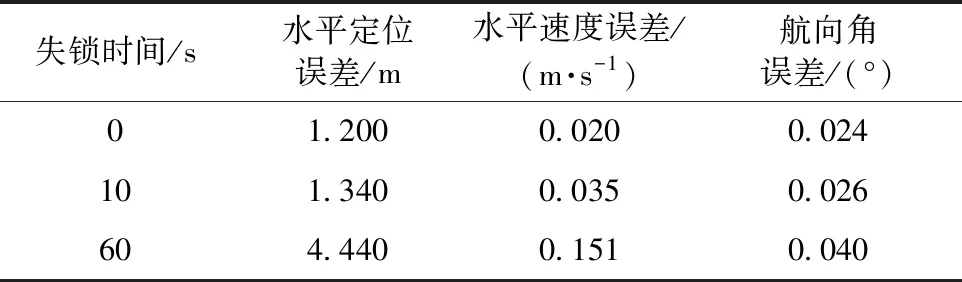
表4 SPAN系统在GNSS失锁条件下的误差

通过对数据结果分析可知，IMU误差补偿前后航向角、速度的结果对比见图8、图9。

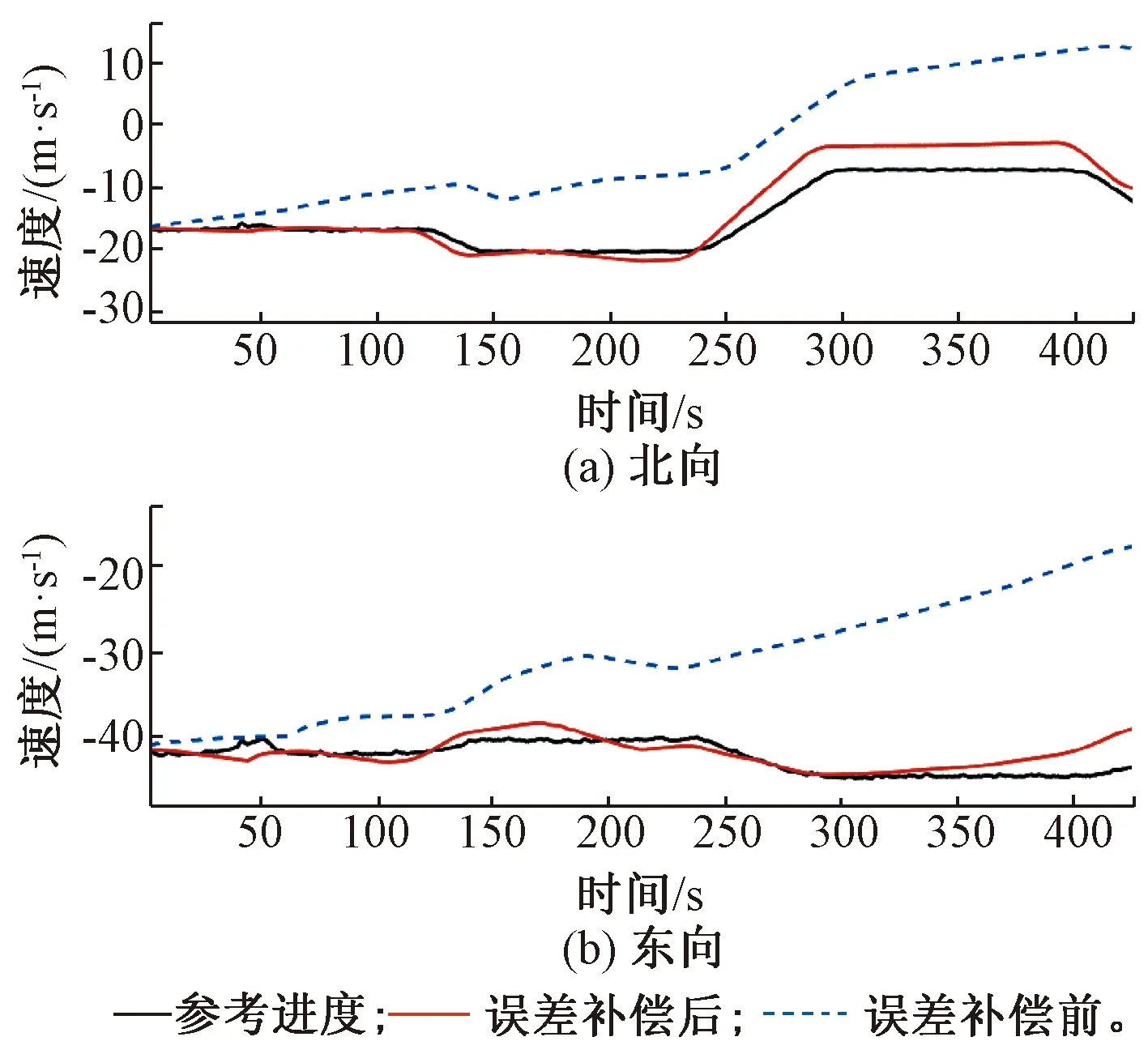
图8 速度对比

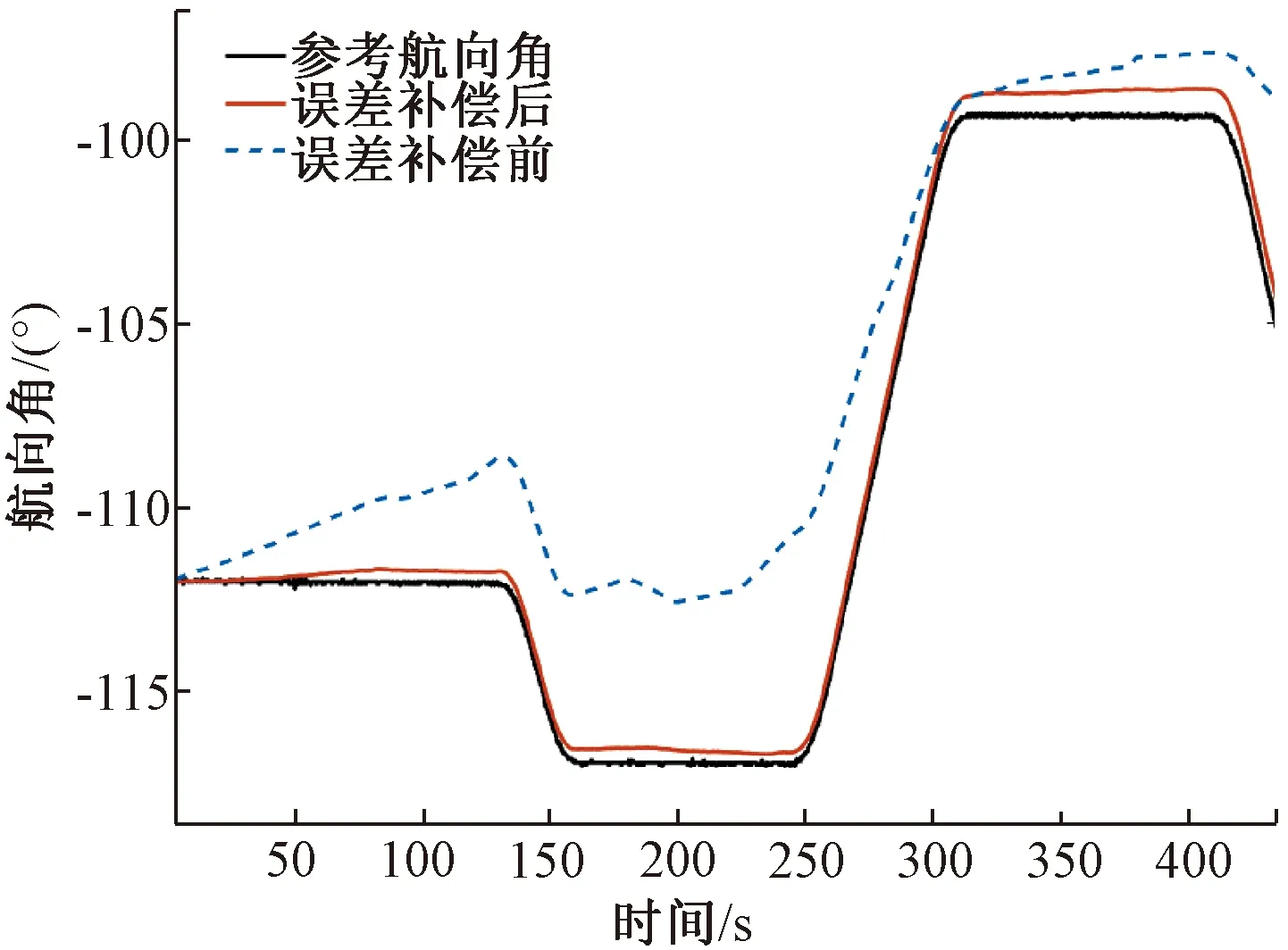
图9 航向角对比

从图8、图9整体来看，经过420 s的导航解算，惯性器件误差未补偿之前的速度、航向角均和真实值有较大误差：东向和北向的速度全程与实际速度不吻合并且最终误差均大于20 m/s；航向角在100～250 s内误差大于5°，整体误差较大。而补偿之后的速度曲线和实际速度曲线相对吻合，北向和东向速度误差最大均为2 m/s左右，航向角最大误差为0.8°。说明补偿之后的航向角和速度相较于未补偿的结果有了较大的提升。

图10是IMU误差补偿前后列车运行轨迹示意图，可以直观地看出误差补偿后列车运行轨迹更加贴合实际线路轨道。具体的列车水平位置误差见图11，可以看出经过补偿的位置误差累积较慢，动态下补偿效果明显。

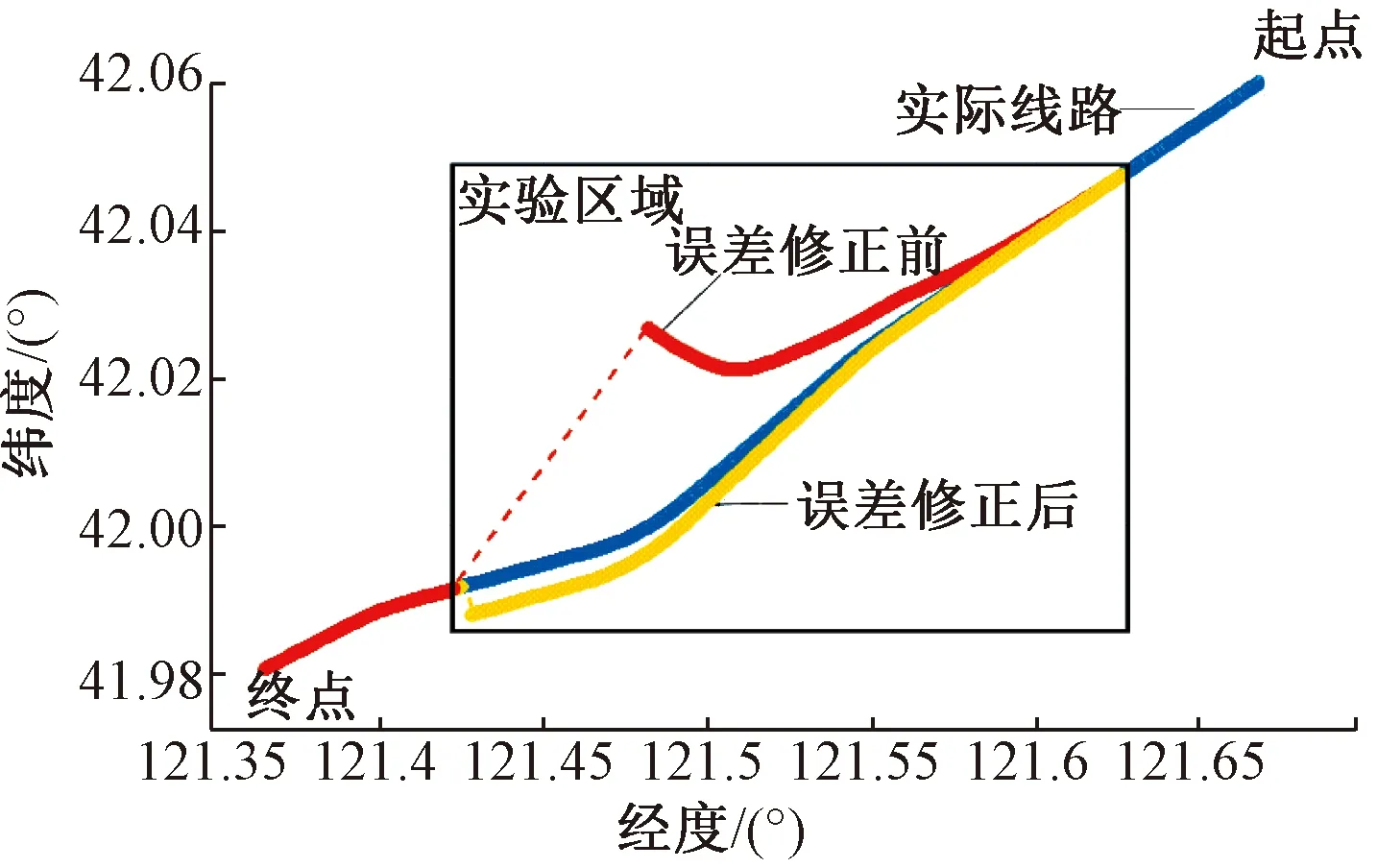
图10 列车运行轨迹

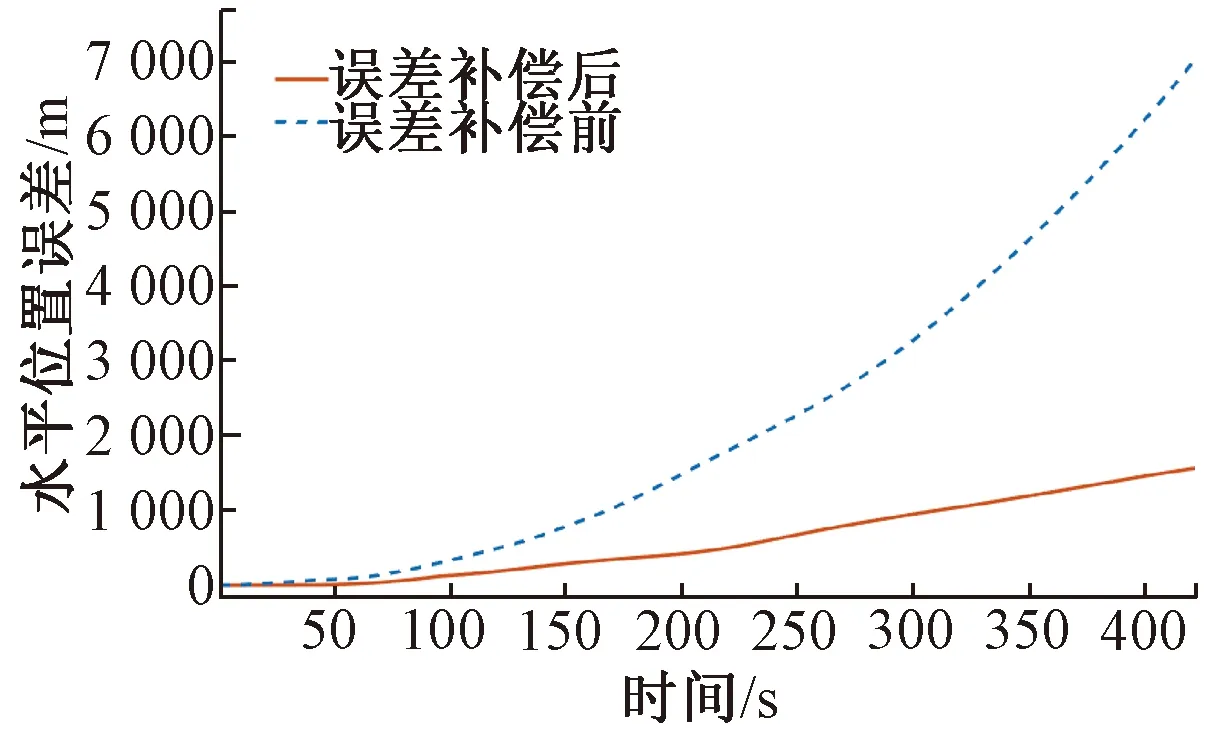
图11 水平位置误差对比

表5总结上述速度、航向角和位置误差，具体列出了GNSS失锁后第10、40、60 s误差补偿之后的各项误差。

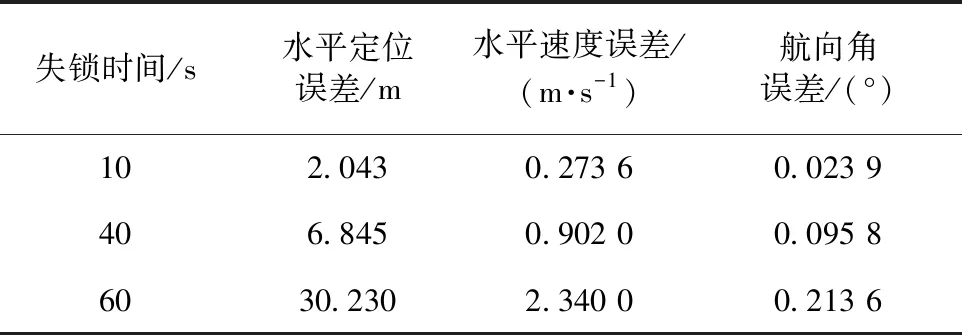
表5 误差补偿之后GNSS失锁条件下误差

可以看出，经过误差补偿之后，列车运行过程中在卫星信号完全失效40 s内能将速度误差控制在1 m/s之内，位置误差为6.845 m，而目前卫星导航也仅提供10 m级的定位精度[15]，相较于该系统，本文研究的误差补偿方法应用于MEMS捷联惯导系统在40 s内的定位精度与其相当，满足铁路应用需求。可以说，经过了误差补偿之后，延长了自主导航精度的保持时间,在不改变硬件的条件下，本方法不仅有利于提高组合导航的定位精度，还加强了组合系统在复杂环境的适应能力。

4 结束语

在现有的MEMS惯性器件精度基础上，误差补偿修正是提高导航精度的有效办法之一。本文为了解决列车车载设备应用GNSS/INS组合导航时，在经过林区、隧道等复杂环境时定位精度下降的问题，针对惯性器件的安装误差、标度因数、零偏误差进行建模，利用12位置法辨识加速度计的误差参数，并利用多速率正反转标定方法降低地球自转及其他外界因素对陀螺标定的影响，并详细推导标定原理，设计编排标定方案。通过将该结果应用于京沈高铁现场，由回放数据的分析结果可知，利用上述方法可以使低成本的MEMS-IMU测量精度明显提高，进而使MEMS捷联惯导系统能在卫星信号失锁40 s的时间内定位精度依旧满足铁路定位系统的需求。由于该误差补偿的方式能有效地降低定位误差，操作步骤也简单易执行，具有实际的工程应用价值。

当然，本文通过对IMU的补偿仅考虑了三项误差，环境带来的各项随机误差影响也不可忽视，通过对数学模型的改善并且在列车运行期间动态标定IMU，将极大改善定位精度。