波浪理论及其适用范围的探讨

海洋广袤无垠且极其神秘，可以给人类带来丰富的渔业、矿产资源和各种能源。但同时海洋又具有强大的破坏力，海上风浪可以毁船亡人，破坏各种海上工程结构。为了能够安全地利用海洋，近代以来人们不断地对波浪进行研究，因此出现了系统化的波浪理论。

现代波浪理论一般构建于势流理论基础之上，即认为水体无旋、无粘且不可压缩。工程上常根据相对水深的不同，把规则波分为三种状况：水深波、浅水波和介于二者之间的有限水深波。一般而言，认为深水波和有限水深波适用Stokes波理论，浅水波适用椭圆余弦波理论。但实际上对于有限水深波而言，在不同的水深中，根据波浪的相对波高不同，波浪的形态会发生变化，同样会出现椭圆余弦波的形态，简单地适用Stokes波理论会造成数值分析地错误。为此，本文将对两种规则波理论的适用进行讨论分析。

1.两种规则波理论简介

Stokes在1849年提出了Stokes理论。这种理论主要是通过波陡ε（以波高与波长之比）为小参数进行摄动展开，从而建立不同阶次的Laplace控制方程和边界条件，以此求得不同阶次的速度势。Stokes波的一阶理论由于忽略了高阶项，所推导出的波浪为正弦波浪，即线性波理论。二阶以上的Stokes理论则在不同程度上考虑了非线性的影响，波浪形态会发生变化。但对于浅水区的波浪，受水深影响显著，波浪形态发生巨大变化，Stokes理论会产生相当大的误差，因此Korteweg和 de Vries在1895年首次提出了以椭圆余弦函数来表示的浅水非线性波浪理论—椭圆余弦波理论。从KDV方程出发，并进行相应的数学推导可得到椭圆余弦波的波面函数。在推导过程中，很容易发现，影响椭圆余弦波非线性的参数是Ursell数，以相对波高与相对水深的平方的比值来体现的。

2.椭圆余弦波理论与Stokes波理论的界限讨论

由于波浪理论划分范围的基础是相对水深的大小，因此可将二阶Stokes理论波面对相对水深kd求导，进行分析。二阶无量纲Stokes波波面方程为

其中，G2为二阶周期项的传递函数，即

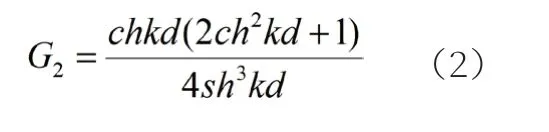
如果要让波面保持Stokes波的性质，即二阶周期项的幅值只和波陡k A有关，与相对水深kd无关，需要将上式对相对水深kd求导，并使导数趋近于0。

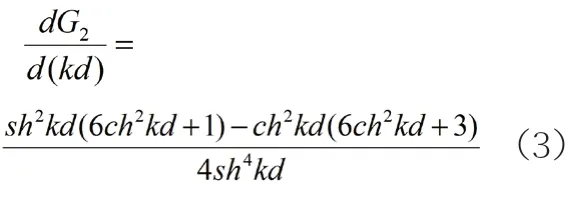
该函数的曲线如图1所示。

由图1可以看出，当kd≥1.4时，式（3）的值几乎为0，即二阶波幅与kd无关，此时只有波陡可以影响波浪的非线性，即完全适用Stokes波理论。

当kd＜1.4时，式（3）的值显然不为0，表现出非线性波浪的幅值要受到相对水深kd的影响，但是影响的大小需要进一步分析。下面举例说明：如图2所示，若k A=0.05时，在kd＜0.8的范围内，kd对幅值的大小有着明显的影响，此时采用只以波陡为非线性参数的Stokes波理论便会使结果失真；若kd＞0.8，kd几乎不影响波浪的非线性，此时使用Stokes波理论便比较合适。若波幅减小，如kA=0.008，此时kd大约以0.5为分界线，左侧需要考虑相对水深的影响，应采用椭圆余弦波理论，而图像右侧kd对结果影响不大，可采用Stokes波理论。

通过以上分析及两张图的比较可得到一个初步结论：当水深较浅时（如kd＜0.8），水深越小，Stokes波理论越只能在更小的波幅范围内适用。那么，在水深一定的情况下，Stokes波理论的适用范围应该取在多大波幅范围内需要更进一步的讨论。

在二阶Stokes波面表达式中，当kd＜0.8时，可以认为shkd≈kd，chkd≈1，则式（1）可改写为

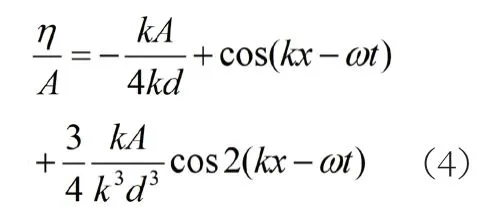
为了让上式满足Stokes波理论的要求，高阶项（右侧第三项）需为小量，其系数应满足

以上结论便成为判定Stokes波理论在有限水深中的使用依据。此外，也因此而定义了判断椭圆余弦波非线性大小的Ursell数，

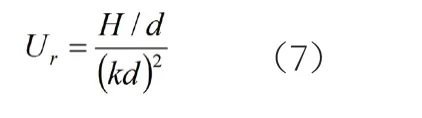
这样，可由Ursell 数判定理论的适用范围。在有限水深中（kd∈[0.3，0.8]时），当Ur＜＜1时，应采用Stokes理论；否则，应采用椭圆余弦波理论。

美国海军海岸工程研究中心曾发布了《The Shore Protection Manual（1984）》，给出了Stokes 波理论、椭圆余弦波理论等相应的适用范围，如图3所示。该图较好地反映出有限水深范围内相对水深kd和相对波高kH对波浪形态的影响，其结果与本文分析基本一致。

3.结论

Stokes波理论和椭圆余弦波理论作为非线性波浪理论的重要组成部分，理论表达、非线性参数完全不同，但两者的适用范围存在交叉，并泾渭分明之界限。首先，不能简单地认为有限水深波浪一定适用Stokes波理论。其次，应当充分考虑kd和k A 的关系，选用合适的理论。最后，最重要的是处理两种理论适用范围交叉区域内的波浪。在该区域内的波浪适用不同理论，会得到截然不同、甚至完全相反的结果，因此，应更谨慎地进行不同理论的适用对比。

图2 二阶Stokes波不同波幅对相对水深求导的函数图像

图3 《The Shore Protection Manual（1984）》给出的波浪理论适用范围