50 kg/m钢轨6号对称道岔脱轨分析及结构优化
李文博
(中铁宝桥集团有限公司,陕西宝鸡 721006)
1 概述
在铁路货运站场中,易发生脱轨的50 kg/m钢轨6号对称道岔一般铺设于编组站驼峰峰顶下咽喉处,往往和小半径曲线及较短的夹直线相连,线路条件较差,且该处车辆溜放速度在站场中是最高的,针对国内对称道岔存在的脱线问题,目前主要有以下措施缓解脱轨现象:
1)加强现场的养护、打磨。2)尖轨涂抹润滑脂、减小摩擦系数、降低脱轨系数。3)降低转辙器部分横向刚度,增大车轮过岔时轨距扩张,可降低脱轨风险。
上述第1,2条措施主要针对现场养护而言,第3条措施是从道岔结构上进行优化,以缓解车辆脱轨现象。在保证岔枕不变、可互换的前提下,对既有的60 kg/m钢轨6号对称道岔轨撑滑床板结构(如图1所示)进行优化,现有滑床板滑床台板采用刚性扣压基本轨,基本轨外侧采用轨撑支撑,其横向刚度较大,车辆通过时尖轨基本轨横向扩张较小,车轮容易爬上尖轨。优化后滑床板在保证扣压基本轨的情况下,提高横向变形,60 kg/m钢轨提速道岔用的弹片销钉式滑床板结构,在提速道岔上已大量使用,结构成熟可靠,本次改进借鉴该结构,改进后滑床板结构型式见图2,基本轨内侧采用弹片扣压,外侧取消轨撑,采用弹条扣压。
针对50 kg/m钢轨6号对称道岔出现的车辆脱轨掉道问题,从道岔结构自身出发,计算车辆通过转辙器前端时的脱轨系数及基本轨的轨距扩张量。

图1 轨撑滑床板结构
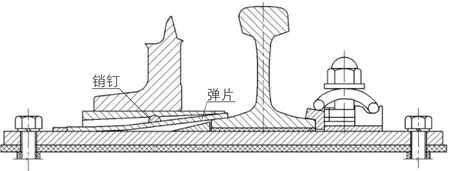
图2 弹片销钉式滑床板结构
2 脱轨系数计算
脱轨系数是指某一时刻车轮作用于钢轨的横向力与竖向力的比值H/P;我国对于常速铁路的脱轨系数规定是H/P的值等于1.2为危险限度,H/P的值等于1为容许限度[1]。
2.1 车辆通过转辙器时的横向力计算
在50 kg/m钢轨6号对称道岔中,设车辆以速度v通过,在车轮由基本轨进入尖轨的过程中,车辆速度将发生如图3所示的变化。

图3 车辆进入尖轨过程中速度的变化
如图3所示,尖轨前端直线段与基本轨的夹角β'为尖轨冲击角,当车轮由基本轨转向尖轨时,由于冲击角的存在,车轮速度的方向被尖轨强制改变,由原来的与基本轨平行的方向变为与尖轨前端平行的方向,在此过程中产生了大小为v sinβ',方向为垂直于尖轨向轨道中心的速度损失,这一部分速度损失正是由于尖轨强制改变车轮运行方向引起的,相反,在此过程中,车轮也会对尖轨产生与速度损失方向相反的冲击。
分析车轮在尖轨尖端的运行轨迹,对于50 kg/m钢轨6号对称道岔,车辆运行方向的改变是在尖轨尖端到尖轨顶宽20 mm这一段完成,该段长度为0.969 m,道岔设计速度为35 km/h。考虑到该道岔主要用于驼峰编组,计算时取最大速度为30 km/h。车轮前进方向被强制改变的时间约为0.116 s,设一个车轴所分担的车体质量为m,6号对称道岔的尖轨冲击角β'的大小为2°04'20″,根据动量定理:

可计算出车轮对尖轨冲击力F的大小为2.58 m。
在车辆通过岔内导曲线时,虽然该道岔设置了6 mm的曲线外轨超高,当车辆以30 km/h的速度通过时,依然存在未被平衡的离心加速度。

其中,R为道岔导曲线半径,180 m;g为重力系数,9.8 m/s2;S1为两轨头中心线距离,在50 kg/m钢轨6号对称道岔中为1 520 mm;由此,可计算出车辆通过曲线时未被平衡离心加速度为0.35 m/s2,因此,车辆通过曲线时的向心力为 0.35 m。
基于质点运动的特性[2]考虑车轮与钢轨之间的作用,则车轮对钢轨的横向力H由车轮速度改变时对尖轨的冲击力和通过曲线时的离心力两部分组成,因此某一点车轮对钢轨的横向力 H 的大小为 2.58 m+0.35 m=2.93 m。
2.2 车轮竖向力
设一个车轴所分担的车体质量为m,则单个车轮的轮载大小为 4.9 m。
2.3 脱轨系数计算
根据以上计算及脱轨系数的定义,当车辆通过50 kg/m钢轨6号对称道岔转辙器前端时,车辆脱轨系数:

通过脱轨系数的计算可以看出,在正常情况下车辆通过50 kg/m钢轨6号对称道岔时不存在脱轨的风险,然而,在车辆的实际运行过程中,引起脱轨的原因有很多,如线路状态不好、钢轨磨损严重等,尤其在编组站驼峰处,当空车溜放时,车轮可能会跳起,导致轮载减小,即使此时横向力不是很大,但脱轨系数增大[3],也可能引起脱轨,我国也以轮载减载率作为判别车辆是否存在脱轨风险的依据,认为轮载减载率 ΔP/P>0.6 即存在脱轨的风险[1]。
3 道岔结构优化后动态轨距扩张的计算
通过脱轨系数计算及脱轨现场分析,认为道岔转辙器部分的横向刚度过大,导致车辆通过时在车轮横向力作用下,轨道无法产生动态轨距扩张,从而导致车轮爬上尖轨也可能是引起车辆脱轨的原因。针对这种可能,对50 kg/m钢轨6号对称道岔转辙器部分的滑床板进行了优化,将原来的滑床板一侧刚性扣压改为弹片销钉扣压方式,同时取消基本轨外侧的轨撑,这种结构在60 kg/m钢轨提速道岔上已经取得了成熟应用,完全可以适应50 kg/m钢轨6号对称道岔。下面运用有限元软件ANSYS建立轨道模型,计算转辙器前端在横向力作用下轨距的动态扩张量。
3.1 计算参数的选取及计算
50 kg/m钢轨6号对称道岔转辙器部分基本轨外侧采用的是 B型弹条扣压,其节点扣压刚度为90 kN/m~120 kN/m,计算采用100 kN/m。
基本轨内侧是采用弹片销钉式的扣压,采用图4的加载方式,利用ANSYS软件建立模型对弹片的扣压刚度进行计算确定。

图4 弹片扣压刚度计算示意图
按照图2所示的约束及加载方式,建立ANSYS有限元计算模型,用Solid95单元划分网格,弹片的弹性模量取2.06E11Pa,泊松比为0.3。分别施加10 kN 和8 kN 的力,计算得到弹片扣压钢轨一端的位移分别为 4.051 mm和3.241 mm,如图5所示为施加8 kN的力后弹片的变形,最后可以得到弹片的节点扣压刚度为2.47 kN/mm。

图5 施加8 k N的荷载时弹片的变形
50 kg/m钢轨6号对称道岔一般为货车通过,取其轴重23 t,则作用于一根钢轨上的竖向荷载为115 kN,通过前面脱轨系数的计算,作用于钢轨上的水平荷载大小取为竖向荷载的0.6倍,大小为69 kN。按照图5所示的加载方式,在ANSYS中建立50 kg/m钢轨的有限元计算模型,假设车辆通过时作用于尖轨上的横向力全部传递到基本轨上,并引起基本轨的横向位移造成轨距扩张,因此计算模型取基本轨,加载及约束如图6所示,基本轨轨肢外侧固定约束,两边轨肢分别施加弹片和B型弹条的扣压刚度,轨下支承刚度取35 kN/mm;在水平荷载作用下,钢轨将会绕非工作边的轨肢转动,从而产生横向的轨距扩张。

图6 钢轨加载及约束示意图
3.2 轨距扩张量的计算
根据TB 2034《铁路轨道强度检算法》提供的关于轨道结构强度检算的连续支承梁模型法,对模型长度取7.2 m,充分消除模型边界效应的影响。采用Solid95单元对钢轨划分网格,用Combin39单元模拟弹片、弹条及轨下支承刚度。钢轨弹性模量取2.1E11Pa,泊松比0.3,计算得到钢轨顶部横向位移如图7所示。
根据有限元计算结果,在对50 kg/m钢轨6号对称道岔转辙器滑床结构进行优化后,当车辆通过转辙器部分时,基本轨由于横向力作用造成的侧翻会引起3 mm的轨距扩张,当车轮轮缘侧向挤压尖轨时,作用于尖轨上的横向力传递到基本轨上后,尖轨基本轨整体会向外侧退让3 mm,使得车轮轮缘爬上尖轨的趋势得到缓解,从而减小脱轨风险。考虑到基本轨挤压轨距块造成的横向位移,基本轨的整体横向位移可达到3 mm~5 mm,因此,结构优化后消除了设置轨撑和刚性扣压引起的基本轨横向刚度过大的问题,减小了由于没有轨距扩张而导致车轮爬上钢轨的风险。
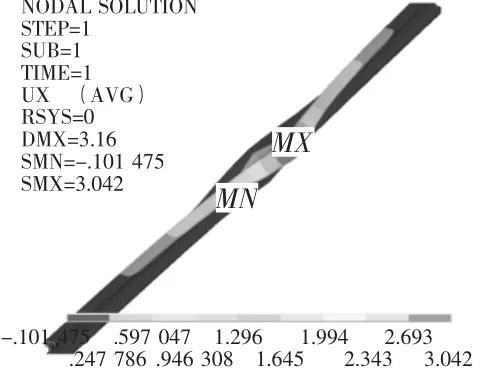
图7 基本轨横向扩张位移计算结果
4 结语
1)在线路和道岔状态良好的条件下,当车辆以30 km/h的速度通过道岔时,车轮的脱轨系数为0.6,理论上不存在脱轨的风险。
2)对50 kg/m钢轨6号对称道岔的滑床板进行结构优化后,减小了基本轨的横向刚度,在车辆通过时会产生不小于3 mm的动态轨距扩大,消除了因为轨距无法扩张而导致车轮挤上钢轨的风险。优化后的道岔在昆明东编组场的应用中尚未发生脱轨事故。
3)造成车辆脱轨的原因比较复杂,除了较大的横向力外,车轮的轮载减载率也是引起车轮脱轨的重要原因,当线路不平顺、轮轨磨耗严重,尤其编组站驼峰处空车溜放时,轮轨系统强烈振动,车轮有跳起的趋势,虽然此时横向力并没有增大,但是车轮作用于钢轨的荷载减小,进而导致脱轨系数增大,产生脱轨的风险。因此,不仅要从道岔结构设计上,更要在道岔的养护维修上重视防范车辆脱轨的风险。

