中外规范关于圆柱壳环向稳定承载力比较

俞栋华 吴金池

(湖北省工业建筑集团有限公司，湖北武汉 430064)

由于各个国家国情不同，钢结构设计分析和计算所依据的标准也有所区别。在钢结构工程中，圆柱壳已被广泛应用于海洋平台、塔桅结构、仓储、容器、烟风管道等。圆柱壳在风荷载或负压作用下容易发生局部失稳。目前，中国规范SY/T 10030—2004［1］中有圆管构件稳定计算的规定，德国规范 DIN 18800 Part 4［2］和欧洲规范 EN 1993－1-6:2007［3］中均有壳体稳定计算的规定。针对圆柱壳失稳这类工程情况，选取不同半径、厚度、长度、边界条件的圆柱壳，分别按照中国、德国、欧洲规范中的相关规定计算稳定承载力，分析总结它们之间的差异。

1 圆柱壳环向稳定承载力计算方法

关于圆柱壳环向稳定承载力计算，文献［1］引入临界环向屈曲系数Ch，该系数考虑了API Spec 2B［4］公差范围之内的初始几何缺陷的影响，未考虑边界条件的影响。文献［2］［3］都是在屈服强度基础上考虑一个折减系数，折减系数考虑了边界条件的影响，且文献［3］引入了与制造质量相关的弹性缺陷折减系数。各国关于圆柱壳环向稳定承载力的具体计算方法如下所述。

1.1 中国规范环向稳定承载力计算方法

根据文献［1］式 3.2.5-6，圆柱壳临界环向屈曲应力计算公式如下:

当 Fhe≤0.55Fy时:

当 Fhe＞6.2Fy时:

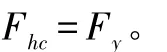
其中，Fhe为弹性环向屈曲应力，根据文献［1］式3.2.5-4计算如下:

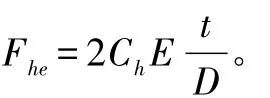
其中，Fy为钢材的屈服强度;E为钢材的弹性模量;D为圆柱壳外径;t为圆柱壳壁厚;Ch为临界环向屈曲系数，根据文献［1］式 3.2.5-5 计算如下:

其中，M 为几何参数，根据文献［1］式 3.2.5-5计算如下:

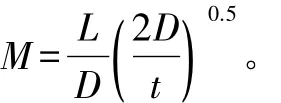
1.2 德国规范环向稳定承载力计算方法

根据文献［2］式44，圆柱壳环向屈曲应力计算公式如下:

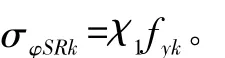
其中，fyk为钢材的屈服强度;χ1为屈曲折减系数，根据文献［2］式7计算如下:

当 λsφ≤0.4 时:

其中，λsφ为通用纤薄度，根据文献［2］式2计算如下:

其中，σφSi为理想弹性临界应力，根据文献［2］式 33～36计算如下:

其中，E为钢材的弹性模量;r为圆柱壳半径;t为圆柱壳壁厚;Cφ为和边界条件有关系数，两端铰支时取1，一端铰支一端嵌固时取1.25，两端嵌固时取1.5。

1.3 欧洲规范环向稳定承载力计算方法

根据文献［3］式8.12，圆柱壳环向屈曲应力计算公式如下:

其中，fyk为钢材的屈服强度;χθ为屈曲折减系数，根据文献［3］式 8.13～8.15 计算如下:

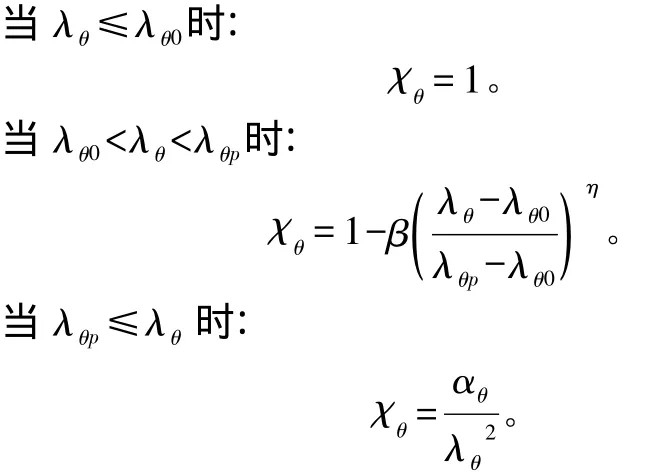
其中，λθ0为极限长细比，取 0.4;β为塑性区系数，取0.6;η 为交互指数，取 1.0;αθ为弹性缺陷折减系数，与制造质量有关，极好时取 0.75，高时取 0.65，一般时取 0.5;λθp为塑性极限相对长细比，根据文献［3］式8.16计算如下:

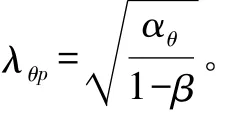
其中，λθ为相对长细比系数，根据文献［3］式8.17计算如下:

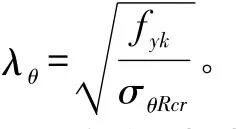
其中，σθRcr为弹性临界应力，根据文献［3］式 D.20～D.25计算如下:

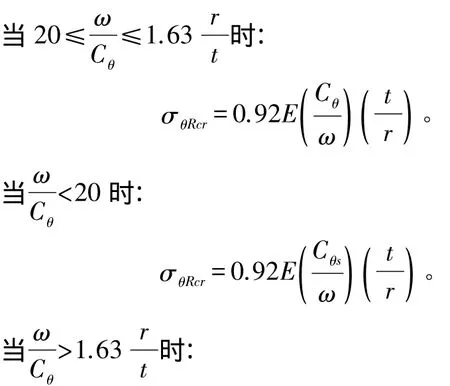
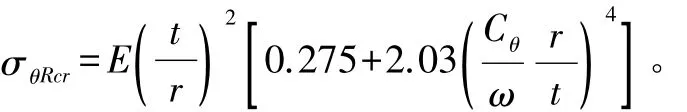
其中，E为钢材的弹性模量;Cθ为系数，两端铰支时取1，一端铰支一端嵌固时取 1.25，两端嵌固时取 1.5;Cθs为系数，按以下要求取值:

其中，ω为无量纲长度系数，根据文献［3］式D.19计算如下:

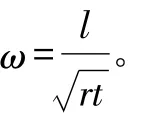
其中，l为圆柱壳长度。

2 圆柱壳环向稳定承载力算例

2.1 不同半径稳定承载力对比

选取厚度为12 mm，长度为7.5 m，边界条件为一端铰支一端嵌固，半径分别为 0.5 m，0.75 m，1 m，1.25 m，1.5 m，1.75 m的圆柱壳，根据文献［1］～［3］计算方法，分别计算各自环向稳定承载力，制成不同半径圆柱壳稳定承载力统计表，见表1。

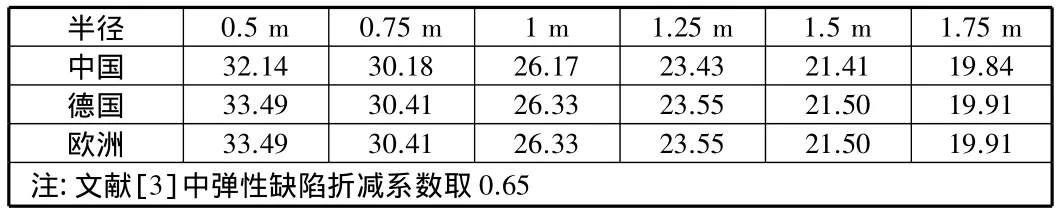
表1 不同半径圆柱壳稳定承载力 MPa

根据表1数据，制成不同半径圆柱壳稳定承载力折线图，见图1。

图1 不同半径稳定承载力折线图

由图1可知，中国、德国、欧洲规范计算的稳定承载力基本相等，且均与半径成反比。

2.2 不同厚度稳定承载力对比

选取半径为1 m，长度为7.5 m，边界条件为一端铰支一端嵌固，厚度分别为 8 mm，10 mm，12 mm，14 mm，16 mm，18 mm的圆柱壳，根据文献［1］～［3］计算方法，分别计算各自环向稳定承载力，制成不同厚度圆柱壳稳定承载力统计表，见表2。

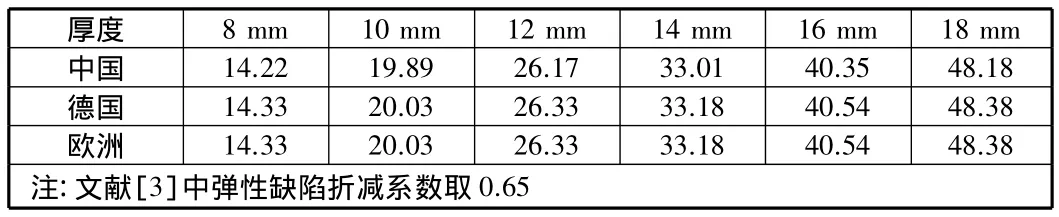
表2 不同厚度圆柱壳稳定承载力 MPa

根据表2数据，制成不同厚度圆柱壳稳定承载力折线图，见图2。

图2 不同厚度稳定承载力折线图

由图2可知，中国、德国、欧洲规范计算的稳定承载力基本相等，且均与厚度成正比。

2.3 不同长度稳定承载力对比

选取半径为1 m，厚度为12 mm，边界条件为一端铰支一端嵌固，长度分别为 2.5 m，5 m，7.5 m，10 m，12.5 m，15 m的圆柱壳，根据文献［1］～［3］计算方法，分别计算各自环向稳定承载力，制成不同长度圆柱壳稳定承载力统计表，见表3。

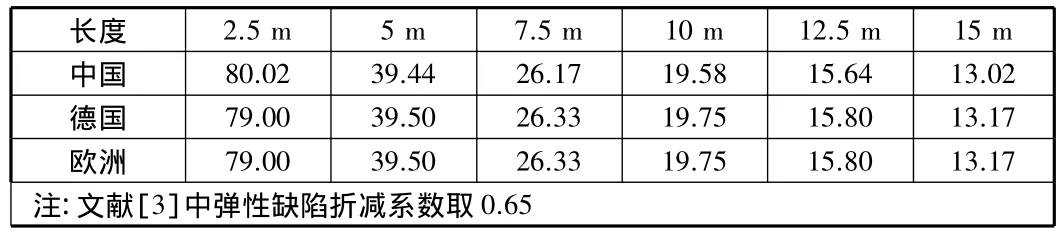
表3 不同长度圆柱壳稳定承载力 MPa

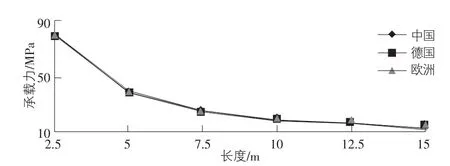
图3 不同长度稳定承载力折线图

根据表3数据，制成不同长度圆柱壳稳定承载力折线图，见图3。由图3可知，中国、德国、欧洲规范计算的稳定承载力基本相等，且均与厚度成反比。

2.4 不同边界条件稳定承载力对比

表4 不同边界条件圆柱壳稳定承载力 MPa

选取半径为1 m，厚度为12 mm，长度为7.5 m，边界条件分别为两端铰支、一端铰支一端嵌固、两端嵌固的圆柱壳，根据文献［1］～［3］计算方法，分别计算各自环向稳定承载力，制成不同边界条件圆柱壳稳定承载力统计表，见表4。

根据表4数据，制成不同边界条件圆柱壳稳定承载力折线图，见图4。

图4 不同边界条件稳定承载力折线图

由图4可知，中国规范计算的稳定承载力与边界条件无关，德国、欧洲规范计算的稳定承载力两端嵌固时最大、一端铰支一端嵌固时次之、两端铰支时最小。当半径、厚度、长度已定，两端铰支时，德国、欧洲规范计算的稳定承载力相等且小于中国规范计算值;一端铰支一端嵌固时，中国、德国、欧洲规范计算的稳定承载力基本相等;两端嵌固时，德国、欧洲规范计算的稳定承载力相等且大于中国规范计算值。

3 结语

1)中国规范计算的稳定承载力未考虑与边界条件的关系，计算结果与实际值存在差异。2)德国规范计算的稳定承载力与欧洲规范中弹性缺陷折减系数取0.65时计算值相等。当边界条件为一端铰支一端嵌固时，德国、欧洲规范计算的稳定承载力与中国规范基本相等。3)中国、德国、欧洲规范计算的稳定承载力均与半径成反比、与厚度成正比、与长度成反比。4)当半径、厚度、长度已定，中国规范计算的稳定承载力与边界条件无关，德国、欧洲规范计算的稳定承载力两端嵌固时最大、一端铰支一端嵌固时次之、两端铰支时最小。两端铰支时，德国、欧洲规范计算的稳定承载力相等且小于中国规范计算值;一端铰支一端嵌固时，中国、德国、欧洲规范计算的稳定承载力基本相等;两端嵌固时，德国、欧洲规范计算的稳定承载力相等且大于中国规范计算值。