城市公交线路运行可靠度分析及优化
王梦琪 蒙素兰 程铅 杜文凯 林淦
(河海大学土木与交通学院,江苏南京 210098)
1 研究背景
随着城市交通的发展,大力发展公共交通已成为共识。公交在运营过程中由于受到天气状况、道路状况等众多因素的影响,运行可靠度较差,具体表现为各站点到达或发车不准时、串车现象严重等问题。因此,需要从公交站点是否发生串车现象的角度考虑,判断公交路线运行可靠性高低,并借此优化公交运行。针对公交运行可靠性的研究,Avishai从可靠性的内涵出发,将公交服务可靠性定义为在一段时间内提供稳定服务的能力[1]。Tumnquist等提出公交服务可靠性是遵守时刻表或者保持规律的到站间隔的概率[2]。魏华构建了公交服务水平评价体系,并将可靠性定义为:公交系统在道路动态交通条件下,能够完成载客任务、给乘客提供一定水平服务的能力[3]。宋晓梅等借鉴可靠性理论定义了公交运行可靠性,从定性的角度分析了影响公共交通运行可靠性的因素,并针对这些因素提出了相应的改善策略[4]。针对公交运行可靠性的研究,评价指标的选取、可靠性评价等方面还不完善,需要进一步深入研究。故本文通过分析公交站点的串车现象评价公交线路运行稳定性并进行优化。
2 公交线路运行可靠性分析及优化模型建立
2.1 时段划分
由于道路交通的潮汐现象,公共线路行程时间会有时段变化特征,为避免或减弱这种现象的影响,本文将公交一天的运行时间划分为几个时段,如表1所示。

表1 时段划分结果表
2.2 评价指标选取
对于公交站点,串车现象是最直接反映公交站点可靠性的指标,而公交站点的可靠性又能进一步反映该公交线路运行可靠性高低,故选取判断串车现象发生频率的指标对公交运行可靠性进行分析。
根据《公共交通通行能力和质量服务手册》中对串车现象的描述——当实时的车头时距大于计划车头时距的1/2时,即可判断为串车现象。故选取车头时距变异系数Cov(h)对公交站点串车现象进行分析。
2.3 公交运行数据集搭建
通过公交实际运行数据对三个不同时段分别搭建数据集,包括每相邻两辆公交车到达各站点的车头时距及其平均值和标准差。
2.4 构建公交串车现象判断模型
2.4.1 计算公式
车头时距变异系数Cov(h)的计算公式如式(1)所示:

其中,Cov(h)为车头时距变异系数;Sh为车头时距的标准差;Dh为车头时距的平均值。
2.4.2 判断标准
判断公交站点是否发生串车现象的标准为,Cov(h)的值为0.00~0.21表示公交到达站点的车头时距与规定值非常一致,为0.22~0.30表示公交到达站点的车头时距稍偏离规定值,为0.31~0.39表示公交到达站点的车头时距经常偏离规定值,为0.40~0.52表示公交到达站点的车头时距波动大,部分车辆串车,为0.53~0.74表示公交到达站点会经常性串车,不小于0.75表示该站点绝大部分的车辆处于串车状态。数据来源:Transit Capacity and Quality of Service Manual-3rd Edition.
2.5 判断公交站点是否发生串车现象
2.5.1 指标计算
根据数据集中的数据通过式(1)计算不同时段内不同发车时间间隔下各站点的车头时距变异系数Cov(h)。
2.5.2 串车现象判断
通过计算出的车头时距变异系数Cov(h)的数值,判断在不同发车时间间隔下公交站点是否发生串车现象以及发生串车现象的频率。
2.5.3 优化方法
若该时段内在所有发车时间间隔下各公交站点发生串车现象的频率较高,则选取发生串车现象最少的发车时间间隔作为该时段最佳发车时间间隔,将该时段内公交发车时间间隔统一为该最佳发车时间间隔。
若该时段内在所有发车时间间隔下各公交站点发生串车现象的频率都很低,则说明该时段内该公交路线的公交运行可靠性高,无需进行优化。
2.6 验证优化方法
若对某时段内的公交发车时间间隔进行调整,以此来优化该公交路线的运行可靠性,则需要再次通过式(1)对该线路上各公交站点的车头时距变异系数Cov(h)进行计算,并进一步判断各公交站点发生串车现象的频率,以此判断通过调整发车时间间隔的优化方法是否有效。
3 实例验证
3.1 公交线路选取
选取南京市3号公交路线(往山西路方向)进行研究,该线路起始站以及终点站均为随家仓,为环形公交线路。
3.2 数据选择及指标计算
通过对选取线路进行实地公交运行数据调查,选取早高峰这一时段的数据集进行分析。
选取早高峰公交运行数据集G1中发车时间间隔分别为5 min,4 min的数据,计算对应的各站点的车头时距的平均值、标准差和车头时距变异系数Cov(h),分别见表2,表3。
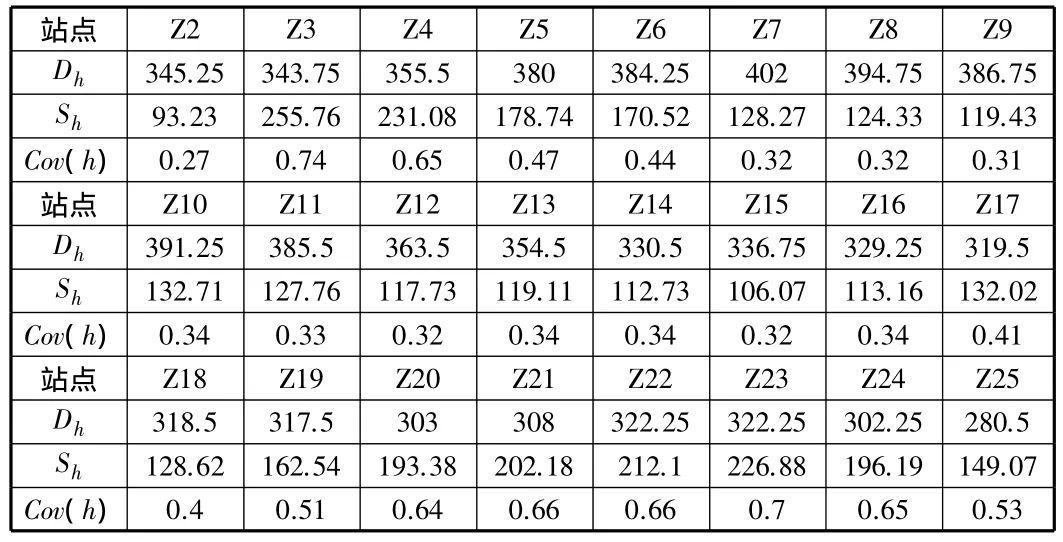
表2 发车间隔5 min数据计算表

表3 发车间隔4 min数据计算表
表中Z2表示该公交路线上的第2个公交站点,起始站为第1站。
3.3 串车现象分析及优化
根据表2可以看出,早高峰该公交路线发车时间间隔为5 min时,该公交线路上大部分站点的车头时距变异系数Cov(h)的值在0.31~0.39之间,根据评价标准,说明公交车在该站点的车头时距经常偏离规定值。还有一大部分站点的车头时距变异系数Cov(h)的值在0.53~0.74之间,说明该站点会有经常性的串车现象。故可以判断该公交线路上大部分站点会经常产生串车现象,说明该公交线路公交运行可靠性低,需进行优化。
据表3可以看出,早高峰该公交路线发车时间间隔为4 min时,该公交线路上大部分站点的车头时距变异系数Cov(h)的值在 0.00~0.21 之间,部分在 0.22~0.30 之间,根据评价标准,说明公交车在该站点的车头时距与规定值基本一致,有时会稍微偏离规定值,进一步说明早高峰时段内发车时间间隔为4 min时该公交路线的公交运行可靠性高。
根据两个发车时间间隔下该路线公交运行可靠性的高低比较,可知在早高峰时,若将所有公交车辆的发车时间间隔均调为4 min,会减少公交站点串车现象的发生,提高公交运行可靠性。
4 结论
本文通过对一天中划分的各个不同时段内公交线路上各公交站点发生串车现象的频率进行分析,判断某时段内公交路线运行可靠性高低,在此基础上,对可靠性低的时段进行发车时间间隔调整,不断调整发车时间间隔,直至找到使公交线路运行可靠性最高的发车时间间隔。该模型及优化方法有效地降低了公交站点发生串车现象的频率,提高了公交线路运行可靠性,对减缓交通流拥堵问题具有一定现实意义。

