对一类函数模型f(x)=ax+blnx+c的探究
孟 彪 许章永
(江苏省南京师范大学附属扬子中学 210048)
一、模型解析
通过对历年高考题及联考题、模拟题的分析可以发现,各地区高考、模拟考压轴题多以lnx、x、ex通过组合得到新的函数模型,本文将其抽象为f(x)=ax+blnx+c模型.这种模型看着复杂、难解,但是著名数学家华罗庚先生曾说过:对于复杂的问题要善于“退”,足够地“退”,“退”到最原始而不失重要性的地方,是学好数学的一个诀窍.
笔者所在学校于2019年10月开展了一场南京市专家视导教学,本次视导教学的主题是:研究函数f(x)=ax+blnx+c模型.笔者将这次视导的内容和研究心得整理后呈现给大家,供大家参考.为了研究的方便,先从模型的一种简单形式开始研究,令模型中的a=1,b=-1,c=-1进行研究.
问题探究f(x)=x-lnx-1,x∈(0,+)的性质.
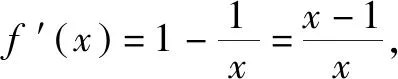
(1)函数:f(x)=x-lnx-1≥0恒成立,(2)不等式:x-1≥lnx,(3)方程:x-lnx-1=0的根是1.以上从函数、不等式、方程三个方面对模型进行分析研究.
将x用ex替换可得ex≥x+1,进一步又可以得到ex≥x+1>x>x-1≥lnx.这个不等式串是压轴题中常用的放缩形式.几何意义如图1所示:

评注让学生课前先探究f(x)=x-lnx-1,x∈(0,+)模型,课堂上加以引导可以得到函数、方程、不等式三者之间的关系,然后让学生将x用ex替换可得到一系列不等式串,这是从数的角度理解,为下面的专题中的放缩作铺垫,再引导学生从形的角度加以解释,即得到图1的函数图形.
本文通过一个典型的例题来阐述这一函数模型:f(x)=ax+blnx+c,然后进行推广,例题如下:
例1 已知函数f(x)=ax-lnx-a,
(1)若函数f(x)≥0恒成立,求a的值;
(2)若a>0时函数f(x)有且只有一个零点,求a的值;
解析(1)问,方法1:分参,f(x)≥0⟺a(x-1)≥lnx.
当x=1时,f(x)=0,此时f(x)≥0恒成立.综上,a=1.
方法3:数形结合法,a(x-1)≥lnx可以理解为函数y1=a(x-1)图象在y2=lnx的图象上方,由图2可知a=1时y=x-1是y=lnx在(1,0)处的切线,a为其他值均不满足.
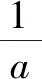
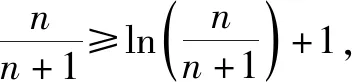
评注本题常规做法学生首先会想到用数学归纳法来证明,但是证明过程繁琐、易错,这里不再呈现.但是如果知道探究的两个不等式模型就可以快速构造函数解决问题.
二、模型推广
函数模型f(x)=ax+blnx+c中的x用x2代替,可得f(x)=ax2+blnx2+c,化简可得f(x)=ax2+2blnx+c,进而可以将模型的次数升高、形式复杂化,这种形式备受命题者青睐.将f(x)=ax+blnx+c中的x用ex代替可得f(x)=aex+blnex+c将其化简变形可以得到f(x)=aex+bx+c,由此得到x、ex的组合函数形式.无论如何变化,但“万变不离其宗”,本源还是来至于模型:f(x)=ax+blnx+c.因此,只要将本模型f(x)=ax+blnx+c研究透彻,就可以解决这一系列问题.
三、考题再现
例1(2017年高考全国Ⅱ卷理数)已知函数f(x)=ax2-ax-xlnx,且f(x)≥0.
(1)求a;(2)略.
解析本题中f(x)看着形式比较复杂,直接分参或者讨论单调性均难以得到正确答案,但是分析发现,只需要对f(x)形式稍作处理就能快速得到答案,f(x)=x(ax-a-lnx)≥0,x>0可以转化为f(x)=ax-a-lnx≥0,x>0,同例1(1)问,这里不再赘述.
评注洞察题目的本质,发现其本源所在是提高解题能力必不可少的一步,本题稍加处理后即转化为例1研究的模型,一个复杂函数问题可转化为一个熟悉、简单的模型,问题迎刃而解.
例2 (湖北省武汉市2012年高三调研)已知函数f(x)=lnx-kx+1.
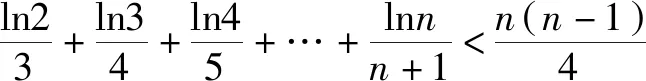
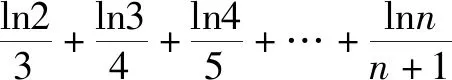
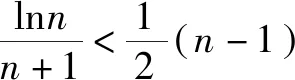
lnx
评注本题证明题看着形式很复杂,学生遇到后很可能第一选择是数学归纳法,但是证明复杂,不易得分,如果洞悉本题的本质,只需构造一个不等式模型即可解决,而这个不等式正是探究中研究过的形式,下面的解题思想与例1(3)思想如出一辙.
例3 (2019年南京六校联合体考试)已知函数m(x)=x2,函数n(x)=alnx+1,a∈R.若函数f(x)=m(x)-n(x)有且只有一个零点,求实数a的取值范围.
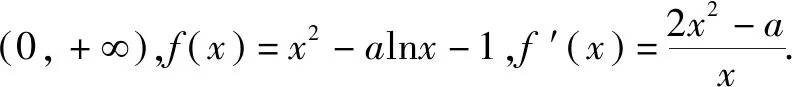
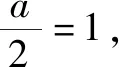
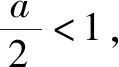
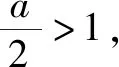
综上,a∈(-,0]∪{2}.
评注本题的难点在于突破“隐零点”,(ⅱ)中利用“局部为零法”思想发现令x=e-1/a时f(x)的值大于零,由零点存在定理可知不符合题意,这里x还可以取e-1/2a,e-1/3a,….对于(ⅲ)需要找出f(x)大于零的部分,常规做法很难处理,但是利用本探究的“不等式放缩法”lnx≤x-1很轻松地就能解决问题.
例4 (2018 年全国新课标卷Ⅰ)已知函数f(x)=aex-lnx-1.
(2)证明:当a≥e时,f(x)≥0.
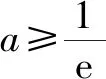
评注本题表面来看是由lnx、x、ex组合而来的复杂形题目,但是分析后利用“不等式放缩法”转化为本文探究的模型.因此,本体的主要工作就转化为证明构造的不等式,而这个不等式的证明很简单.
四、反思总结
以上通过具体实例阐述了函数模型f(x)=ax+blnx+c,并得到两个常用不等式:x-1≥lnx,ex≥x+1.可以用这两个不等式解决恒成立问题、“隐零点问题”、“极值点难求问题” ,证明数列不等式等.在历年的各类考试中, 压轴题以lnx、x、ex组合为背景命题,屡见不鲜, 值得广大师生重点关注.而在解决此类问题时, 需要从多个角度, 发散思维的考虑问题,注意回归本源,不能生搬硬套模型、解题方法和技巧,需要在实践中多次尝试、领悟, 方能在解题中提高自身的能力,达到提升学生数学运算、逻辑推理、数学抽象的核心素养.

