追踪考题 晒晒考点
——“复数”高考考点题型归类析与练
杜红全
(甘肃省康县教育局教研室 746500)
复数是高考的热点内容,以选择、填空的形式出现,题目难度不大.通过对复数历年高考试题的研究,发现考点题型有以下几个方面,供同学们在复习时参考.
一、复数的概念问题
例1(2016全国Ι卷,文2)设(1+2i)(a+i)的实部与虚部相等,其中a为实数,则a=( ).
A.-3 B.-2 C.2 D.3
解析原式=(a-2)+(2a+1)i,由已知得a-2=2a+1,解得a=-3,故选A.
点评本题考查复数的实部和虚部的概念.解此类题的关键是先把原式变形为a+bi(a、b∈R),然后再根据复数的相关概念来求解.
跟踪练习1 (2016江苏,理2文2)复数z=(1+2i)(3-i),其中i为虚数单位,则z的实部是____.
(答案:5)
二、复数的相等问题
例2 (2015全国Ⅱ卷,理2)若a为实数,且(2+ai)(a-2i)=-4i,则a=( ).
A.-1 B.0 C.1 D.2
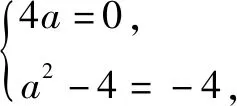
点评解本题的关键是先将(2+ai)(a-2i)进行运算,变形为a+bi(a、b∈R)的形式,然后根据复数相等的条件列出关于a的方程即可.

(答案:2)
三、求复数或共轭复数的问题

A. -1+2i B. 1-2i C. 3+2i D. 3-2i
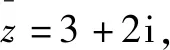

跟踪练习3 (2015全国Ⅰ卷,文3)已知复数z满足(z-1)i=1+i,则z=( ).
A.-2-i B.-2+i C. 2-i D. 2+i
(答案:C)
四、求复数模的问题
例4 (2016全国Ⅰ卷,理2)设(1+i)x=1+yi,其中x,y是实数,则|x+yi|=( ).

点评解本题的关键是根据复数相等的条件列出关于x,y的方程组,求出x,y的值,然后再利用求复数模的公式计算即可.

(答案:A)
五、点的位置问题
例5 (2016全国Ⅱ卷理1)已知z=(m+3)+(m-1)i在复平面内对应的点在第四象限,则实数m的取值范围是( ).
A.(-3,1) B.(-1,3)
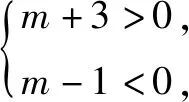
点评解本题的关键是先把复数化为a+bi(a、b∈R)的形式,再根据点所在的象限,列出不等式组求出实数m的取值范围.
跟踪练习5 (2016北京,理9)设a∈R,若复数(1+i)(a+i)在复平面内对应的点位于实轴上,则a=____.
(答案:-1)
六、复数的运算问题

A.1 B.-1 C. i D.- i



A. i B.1+ i C. -i D. 1-i
(答案:A)
七、复数的一元二次方程求根问题

A.b=2,c=3 B.b=-2,c=3
C.b=-2,c=-1 D.b=2,c=-1

点评本题主要考查的是实系数方程根的性质及根与系数的关系、实系数方程的虚根成对,难度不大.
跟踪练习7 (2012湖北,理1)方程x2+6x+13=0的一根是( ).
A.-3+2i B.3+2i C.-2+3i D.2+3i
(答案:A)
八、复数与其它知识的综合
例8 (2015陕西,理11)设复数z=(x-1)+yi(x,y∈R),若|z|≤1,则y≥x的概率为( ).
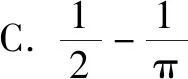


点评本题将复数与几何概型交汇,考查数形结合的思想.解决本题的关键是准确画图,根据图形容易看出面积关系,还省去了求∠OBA,直观看出其大小为90°.
跟踪练习8 (2014浙江,理2)已知i是虚数单位,a,b∈R,则“a=b=1”是“(a+bi)2=2i”的( ).
A. 充分不必要条件 B. 必要不充分条件
C. 充分必要条件 D. 既不充分也不必要条件
(答案:A)

