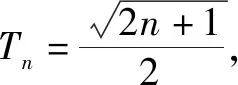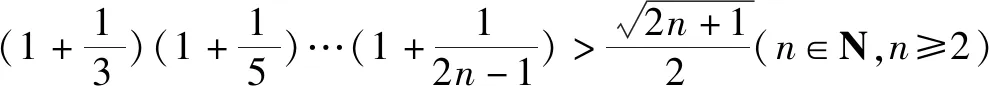构造函数证明数列不等式问题
朱东海
(云南省蒙自市第一高级中学 661199)
在本刊2016年第34期、2018年第10期、2019年第13期中,我们分别谈了一元函数不等式、二元函数不等式和与零点有关的函数不等式的证明方法,本文中我们来看如何构造函数证明数列不等式.
一、项与项之间的不等关系
对项与项之间的不等关系可以先将不等式变形后,直接把正整数n换成x,转化为一元函数不等式来证明.

(1)求函数f(x)的单调区间;
(2)设m>0,求f(x)在区间[m,2m]上的最大值;

解(1)f(x)的定义域为(0,+),

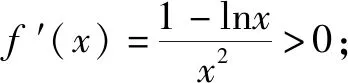
所以函数f(x)在(0,e]上单调递增,在[e,+)上单调递减.

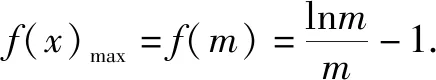

(3)由①知,当x∈(0,+)时,所以在(0,+)上,恒有即且当x=e时等号成立.
因此,对∀x∈(0,+),恒有



二、数列的前n项的和与f(n)的不等关系
1.f(n)不是常数
若f(n)不是常数,则把f(n)看成数列{bn}的前n项的和,求出数列{bn}的通项公式,再用作差或导数等方法证明an与bn的大小关系,最后累加就能得出结论.


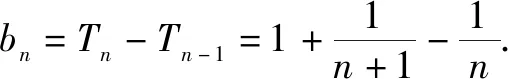
而n≥2时
令f(x)=3x+2-2x(x+1)(x≥2),则有f′(x)=3xln3-4x-2>3x-4x-2.再设
g(x)=3x-4x-2(x≥3),g′(x)=3xln3-4>3x-4>0(x≥3),
∴g(x)在[3,+)是增函数.但g(3)=13,因此当x≥3时,g(x)>0,
也就是说当x≥3时,f′(x)=3xln3-4x-2>g(x)>0,f(x)在[3,+)是增函数,
∵f(3)=25,当x≥3时∴f(x)>0,即n≥3时an>bn.

∴a1+a2>b1+b2.
又当n≥3时an>bn,

在证明an与bn的大小关系时,若能变形,则先变形后再证明.
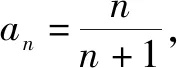

当n≥2时,bn=1+ln(n+1)-ln(n+2),我们只需证明当n≥2时an 令f(x)=ln(1+x)-x(x>0), 而f(0)=ln1-0=0,∴当x>0时ln(1+x) 2.若f(n)是常数 若f(n)是常数,则利用当n取第一个数时,不等式两边之差来加强不等式,再用上述方法证明. 例3 (2008年辽宁高考题第二问)已知an=n(n+1),bn=(n+1)2(n∈N*), ∵(n+1)(2n+1)-(n+2)(n+3)=n2-2n-5=(n-1)2-6, 对于数列{an}的前n项的积与f(n) 的不等关系的证明的一般方法是,把f(n)看成数列{bn}的前n项的积,求出数列{bn}的通项公式,再借助作差或导数等办法来比较an与bn的大小. 而当n≥3时, ∴a4>b3,a5>b4,…,an>bn-1.又a3>an+1>bn, ∴a2>T2,则有a2a3…an>T2b3…bn.
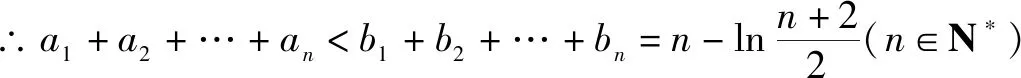





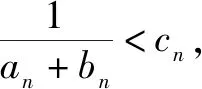

三、数列{an}的前n项的积与f(n) 的不等关系