考虑多级价格折扣的二级分销系统库存成本优化研究

戴浩亮 （上海大学 管理学院，上海200444）

0 引 言

随着物流的发展，越来越多企业逐渐意识到竞争不止局限于企业之间，同时也存在与企业通过合作形成的供应链之间。那么如何在供应链的角度下合理配置库存量是现在急须解决的问题。一直以来，库存成本占到企业总成本的30%左右，如果能很好地解决供应链下库存难题，就能很大地提升供应链的灵活性与机动性[1]。

Banerje 以买卖双方合作的角度，建立一种联合经济批量模型。在确定性条件下，计算买方和卖方的联合总相关成本，以制定合适的订货策略和价格[2]；Diks 和Lagodimos 通过分析安装库存策略和梯队库存策略两种策略，分析供应链中的买卖双方的服务水平与总成本的关系，以便以最小的成本满足预定的外部服务目标[3]；Hsin Rau 建立了多级供应链下易腐产品的集成库存模型，通过对生产率和需求率的灵敏性分析，证明了将供应链作为整体考虑的情况下供应链总成本最优[4]；邵晓峰等人研究了非合作博弈和合作博弈两种情况下的最优经济订货批量，分析比较得出供应链的竞争关键在于供应链各成员能否紧密合作，共享信息， 消除供应链中的不确定性因素[5]。随着库存研究的不断深入，库存控制由原有的单级库存控制方法转向基于整个供应链角度的库存控制方法。

随着消费者需求的日益多样化和多变化，零售商拥有更多的话语权。因此本文在多级库存模型的基础上，对下游分销系统进行研究，并考虑零售商批发价格随着订货数量变化的多级折扣问题。最后利用遗传算法得到总成本最小的最佳经济订货批量。

1 二级分销系统模型

1.1 基本问题描述

在非合作情况下，分销中心与零售商都是从自身的成本最优制定决策，难以实现整体最优。当分销中心与零售商作为供应链的子系统，以供应链整体成本最优为目标，同样也难以实现整体最优。因为分销中心与零售商处于不同的地位。当分销中心降低批发价格时，虽然增加了零售商的利润，但是增加了自身成本；同样，零售商增加订货量时，也会损害到自身利益。因此，不同于普通的多级库存模型，本文更加注重分销中心与零售商之间的互动关系。通过引入多级价格折扣，对增加订货批量的零售商进行价格补偿。并且多级价格折扣的引入也使得模型更加符合实际。

本文研究的对象是使用中心化库存控制策略的下游分销系统，其中包含1 个分销中心和n个零售商，并且使用Q，（ ）

R盘点策略，即零售商和分销中心分别对各自的库存水平进行连续性观察，当库存水平降低到订货点R时开始订货，订货批量为Q[6]。

1.2 基本假设

（1） 在下游分销系统中，订购的产品是单一品种；（2） 零售商对自己的库存水平进行持续监测，当库存水平降低到一定水平时，及时、主动地向上级供应商请求供货；（3） 分销中心能满足零售商的所有供货要求；（4） 零售商每次的订货量小于

其最大的库存容量；（5） 不允许缺货；（6） 不同零售商之间以及同一零售商的不同时期的需求都是独立的；（7） 消费者购

买时间具有随机性且服从泊松分布，且每个顾客的需求是一个随机整数。

1.3 成本模型建立

（1） 分销中心的成本模型

由假设7 可知，单位时间内，第n处的零售商面对的消费者数量服从参数为λ 的泊松分布。假设On为n处零售商的消费者的需求量，f（n，On）为n处零售商的需求量On大于0 的概率，且f（n，On）服从几何分布。所以在单位时间内，零售商n需求量的均值μ 和方差分别为：

因此，零售商n在分销中心提前期内的需求均值和方差为：

同时，根据提前期内的需求可以确定再订货点：

其中：k是服从标准分布的服务水平α 的分位数。

根据周期T期初与期末的库存期望值：

确定周期内，分销中心的期望库存持有成本为：

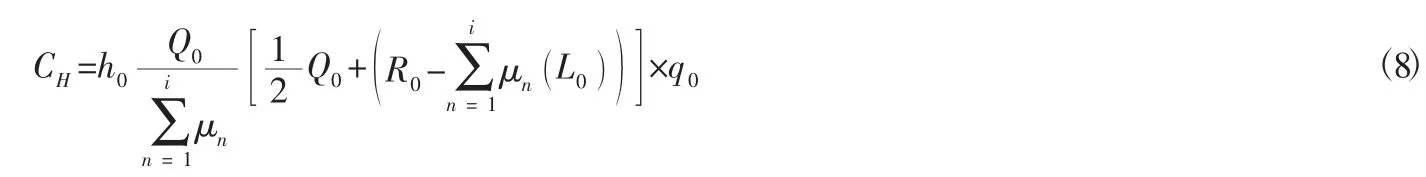
其中：h0为分销商单位库存持有成本率，q0为采购单位产品的费用。

分销中心单次订购产品的数量为Q0，购买单位产品的花费q0，并且单次购买所需要的固定成本为C0，所以订购成本为：

因此，单位时间内分销中心的库存总成本为：

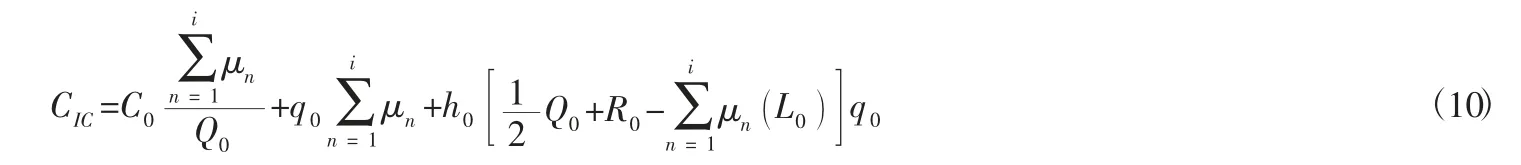
（2） 零售商成本模型

分销中心用于满足零售商的需求，因此，应该考虑到零售商受到分销中心的影响程度。

由于零售商固定向分销中心订货，故产品的价格有折扣。因此在本文中，假设折扣价格与订货量有关，当Qn-v1时，折扣价格为p0；当v1＜Qn ＜v2时，v1单位的货物价格为p0，Qn-v1单位货物的价格为p1；当vi ＜Qn ＜vi+1时，v1单位的货物价格为p0，v2-v1单位货物的价格为p1，vi-vi-1单位的货物价格为pi-1，Qn-vi单位货物的价格为pi。

因此，零售商单位货物的购买费用如下：

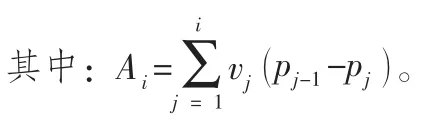
同样，考虑提前期内消费者、分销中心的需求，零售商的再订货点为：

所以零售商n的库存维持成本为：

零售商的订购成本为：

所以零售商n的库存成本为：

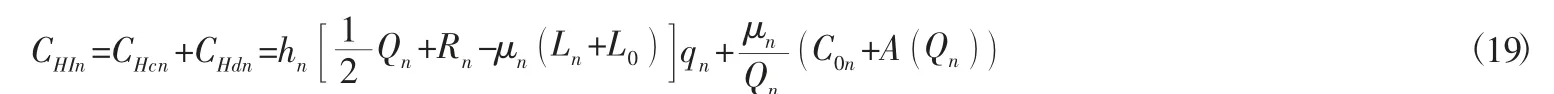
其中：qn为产品批发价格。

因此二级分销系统的总库存成本模型为：

2 遗传算法设计

（1） 确定编码方式。编码是遗传算法首要解决的问题，常见的编码方式有格雷码编码、实数编码、二进制编码、符号编码方式[7]。

（2） 初始化种群。在可行范围内，创造一定规模、数量的随机的原始种群。原始种群中含有个体的数量会对最后的结果产生影响。一般种群的数量在50～200 之间，这里个体数量为100。同时，本文采用最简单和最普遍的产生初始种群的做法，即在各个变量的可行范围内随机产生一定数量的染色体，并以此基础进行迭代。

（3） 确定适应度函数。遗传算法根据适应度来评价解的好坏程度，由于这里成本控制模型的目标是成本最小，而遗传算法的目标为最大值，因此要进行如下转换：

其中：z（x）和Z（x）分别表示目标值和适应度，Cmax是最大的目标值。

（4） 选择与复制。根据适应度函数，计算每个个体的适应度，并且按照某种概率进行选择，将适应度大的个体作为新一轮的父代，开始下一轮的进化。本文采用的是轮盘赌方法来进行选择。

（5） 基因交叉。交叉是指按照某种方法，将两个DNA 交换部分碱基对，相互配对，从而形成新的个体的过程。本文中将交叉概率设为0.8。

（6） 变异。为了产生更丰富的染色体种群，需要通过实值变异来保证实现。

（7） 循环。循环步骤4～6，直到满足终止条件，得到最优解。

3 实证分析

本文选取某物流公司上海地区的分销中心进行研究。该分销中心分配给四家大零售商产品。已知零售商一个月内平均需求为λ1=20，λ2=40，λ3=40，λ4=50。并且零售商n处，消费者需求服从

分销中心提前期L0=1（周），零售商提前期服从正态分布N（0.18，0.01 ），C0=150，C1=C2=C3=C4=120，q0=30，q1=q2=q3=q4=50，h0=0.1，k=1.28，并假设库存约束maxQ0=2 000，maxQ0=800（n= 1，2，3，4 ）。同时，零售商的多级折扣批发价格如下所示：

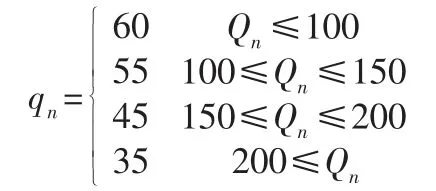
通过遗传算法进行迭代计算，并设置参数：种群规模为100，交叉率为0.8；变异率为0.03；进化代数为500，运用Python 进行求解。可以得到结果如图1 所示：

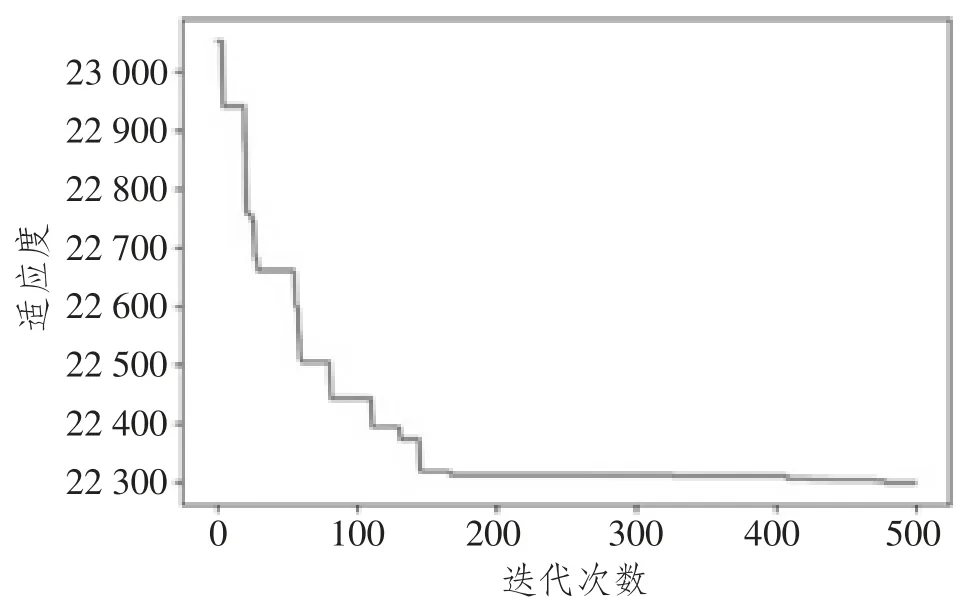
图1 适应度关于迭代次数变化图

从以上运行结果，可以知道分销中心和各个零售商的最优订货批量以及库存总成本。同时在非合作情况下，计算分销中心和零售商的经济订货批量。

（1） 零售商的经济订货批量

由第二小节可知，第n处零售商的成本，并由可得每个零售商的经济订货批量为

（2） 分销中心的经济订货批量

表1 最终结果

4 结 论

企业之间越来越注重供应链的竞争，成本的考虑也不再局限于单个企业。库存作为供应链中重要的一环，过多会导致成本的增加，过少则会影响服务质量。因此，如何合理订货和控制库存成为企业及其供应链需要解决的问题。将分销中心与零售商作为一个整体对总成本进行优化，并考虑分销中心与零售商之间博弈关系引入多级价格折扣。最终应用于某具体企业的库存成本分析之中。结果表明，相较于传统的经济订货批量，本文中的二级分销库存模型能有效减少成本，合理配置各级企业的订货批量。