考虑多成本的多车型多种类生鲜农产品配送模型研究

周 彤，卫少鹏 （贵州大学 管理学院，贵州 贵阳550025）

0 引 言

生鲜农产品容易变质、时效性强、对于运输方面的要求高，现有农产品配送信息化管理不完善、冷链技术较落后[1]，充分考虑影响农产品配送的因素，降低农产品配送成本和时间成为了亟待解决的问题。生鲜农产品属于必需消费品，需求量大、种类多，由于产品本身具有活性，使其在运输过程中对时间、温度等要求较高。同时，生鲜农产品门类众多，可替代消费品很多，如何在市场占据一席之地，除了产品本身质量，价格也是很重要的一个因素。

王邦兆等[2]针对生鲜产品零售点分散而造成成本高的问题，以系统整体的眼光看待生鲜农产品配送并运用遗传算法对整个配送网络进行了优化。范林榜等[3]、高敏等[4]根据农产品在电子商务环境下供应链的发展情况提出了自身看法并提出解决方案，为生鲜农产品双渠道供应链的协调发展提供了理论参考。王淑云等[5]探究了在生鲜农产品库存和利润的影响因素中，保鲜努力水平内在关联性，有利于总利润的提升。黄灏然等找出了生鲜农产品配送环节中的错误现象，并通过错误函数等提出了能够有效避免错误剔除不可行方案模型，有利于提高配送效率。王恒等[6]为了保证生鲜农产品准时到达消费者手中，综合考虑了道路状况、时间窗等因素并运用自适应遗传算法验证有效性。Lu Liu 等[7]考虑消费者对生鲜农产品成熟度的要求，在配送中严格考虑了时间因素，有效地减少了物流损失。Lila Rajabion 等[8]以绿色供应链视野通过模型和问卷数据分析等方法得出了对绿色供应链农产品城市配送成功的因素。Jiani Wu 等[9]开发了一个合适的考虑货运的农产品物流方案，为研究人员和实践者在面对可持续性挑战时处理此类问题提供了实用的指南和见解。Yandra Rahadian Perdana 等[10]提出了农业物流信息系统对供应链管理中的重要性，并叙述了系统所需的体系结构。J.Mehmann 等[11]整合了德国农业散货物流领域第四方物流服务供应商的服务模式，证明了第四方物流服务提供商的方法中采用可持续性供应链管理可以产生额外的价值。Christina Wiederer 等[12]通过对具体国家的农产品物流进行差异分析，为改善吉尔吉斯共和国农产品供应链提出了7 条政策建议。

关于生鲜农产品物流方面的研究，国内外学者大都聚焦于行业整体或归结为车辆路径规划等方面进行优化，大都把生鲜农产品归类为一种东西，但生鲜农产品种类与种类之间差异巨大，受地区、气候、季节等因素影响很大，还少有学者考虑生鲜农产品多种类运输方面的问题。另外，此类研究中采用的运输车辆大都为一种类型，但实际运输当中所用的厢式货车载重量有差别，不同产品所需的车型也有所不同。本文提出多车型多种类农产品配送模型能很好地为实际农产品配送调度提供决策素材。

在目标函数方面，很多学者加入了路况、时间窗、顾客满意等因素，但对于实时路况方面还未有较细致的描述。车辆行驶的成本有固定成本、路径成本、等待成本、过路费等，本文都有考虑。

1 问题描述

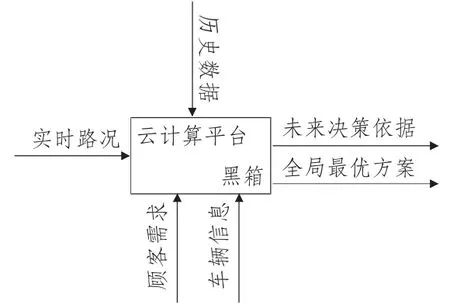
图1 新型地图软件决策模型

路径成本、等待成本等受时间段、季节、天气等因素影响较大，路径选择也会受到实时路况的影响，本文拟提出一种地图类软件的新择优路径模式（如图1 所示）。模型描述：云计算平台黑箱：此实体即地图软件背后的计算平台。实时路况：根据司机及卫星数据记录道路拥堵及道路质量情况。顾客需求：消费者根据需求选择路费、路径及时间。车辆信息：车辆年限、车辆型号、耗油情况、实时运作能耗及磨损等。历史数据：历史数据统计出的堵车及事故等。未来决策依据：堵车信息及车辆运作情况作为今后选择路线的依据。全局最优方案：不止局限于此次行车最短时间或路径，而是基于车辆系统运作及消费者实时需求的全局的、有利于长期出行的推荐路径。在此基础上尽量保证地图数据库的更新和完整。

本文以多种类农产品配送出发，采用多种类车型进行调度，结合实时路况全方位考虑生鲜农产品运输成本，并以此为优化目标，有很强的实际意义。

模型相关解释如下：

（1） 实时路况：考虑等待时间、路径、路费成本的目标函数。

（2） 多车型：多种容量的厢式货车。

（3） 多种类农产品：同时配送一种以上农产品。为了体现多品种运输，本文把厢货车进行分厢，例如载重1.5t 的厢货车，令0.5t 为一个隔厢，每个隔厢可装相同或不同的农产品，理想需求量为隔厢重量的总数。

农产品配送网络：V=｛i、j|0，1，2，3，…，n｝表示零售点的集合，顶点0 表示农产品物流中心是各农产品零售点及物流中心之间的路径集合，dij表示i到j之间的距离；用M=｛m|1，2，3，…，w｝表示农产品集合，零售点对于农产品m的需求量为qim≥0。K表示所有配送车辆的集合，H表示配送中心车辆车型的集合，车型h∈H的固定派车成本为Fh，平均油耗成本为Ch，等待成本为Th，路费成本为Rij，Ah为隔箱集合，研究对象暂为一个周期的配送。为方便研究，假设如下条件：

（1） 订单配送不采取先订先送，均假设各零售商前一天根据销售情况下订单，物流中心第二天统一进行派送。

（2） 假设各种厢式货车每0.1t 为一个隔厢，每个隔厢满载一种农产品，且零售点需求量为隔厢载重的整数倍。

（3） 不同农产品的配送优先级不同，易腐坏、保质期短的先配送，本文假定均为同类型生鲜农产品，不区分优先级。

（4） 配送过程为：物流中心→各零售点→物流中心。

（5） 每个配送过程一旦开始便不中断，不考虑紧急订单插入的情况。

（6） 厢式货车车型为：1.5t、2t、3t、5t。

2 考虑实时路况的多车型多种类生鲜农产品配送模型

决策变量符号说明如下：

Bkh∈｛0，1 ｝，Bkh=1 车辆k∈K属于车型h，否则=0。

Ykaim∈｛0，1 ｝，Ykaim=1 表示车辆k的隔厢a在零售点i需求的农产品种类m，否则=0。

qkaim≥0，表示车辆k的隔厢a在零售点i卸货农产品m的重量。

L

ij表示节点间距离矩阵。

Xij∈｛0，1 ｝，xij=1 表示节点i的下一个节点是j；Xij=0 表示节点i的下一个节点不是j。

tij表示节点间等待成本时间矩阵。

mij表示节点间过路费成本矩阵。

nij∈｛0，1 ｝，nij=1 表示i到j间有过路费；nij=0 表示i到j间无过路费。

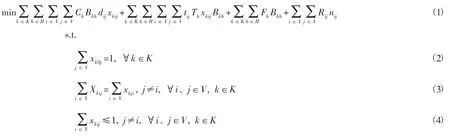
农产品配送模型如上：（1） 为目标函数，表示成本最小，分别包括行驶路程成本、等待时长成本、固定派车成本及过路费成本。（2） 表示所有厢货车均从物流中心出发。（3） 表示厢货车送完一个零售点后离开配送下一个零售点。（4） 表示每个零售点每天只配送一次。（5） 表示厢货车只为经过的零售点进行配送，不接受临时紧急订单。（6） 表示零售点每种农产品需求量不得多于每个隔厢可配送量。（7） 表示每辆车经由的零售点的总需求量不得多于该车的总载重量。（8） 表示每个零售点所需农产品量均被配送。（9） 为适应编程的子回路消除约束。（10） 表示每辆厢货车的每个隔厢只能装一种农产品。（11）表示每辆厢货车型号固定。（12） ～（15） 表示各个变量的约束。

3 基于遗传算法算例分析

生鲜农产品配送问题属于NP-hard 问题，很难短时间运用普通的求解方式得出最优解，本文选用改进型遗传算法进行求解。遗传算法具有并行性、鲁棒性强、利于全局择优等优点，同时也存在易出现未成熟收敛，在快要接近最优值时收敛速度慢、效率低等问题[13]。为了使算法能更好地说明问题，采用实数编码方式。为了使选择算子能兼顾到多样性，让算法的搜索空间大幅度增加，选择锦标赛选择法来进行选择环节。为了增加搜索广度，采用区域重组交叉方法改进交叉算子。改进遗传算法设计如下。

3.1 染色体编码及解码规则

为了更直观地解释改进遗传算法过程，更好地使编码贴近问题，假设为单品种农产品运输，采用实数编码，将所有车辆按照车型排成隔厢等编码，将所需配送的农产品零售点编码。设一个保有6 辆厢货车的农产品配送点给7 个零售点配货，厢货车及零售点信息如表1、表2 所示：

表1 厢货车信息表

表2 零售点信息表

本问题的一个可行解为：2 车负责派送零售点4，路径为0-4-0；4 车负责派送零售点5 和6，路径为0-5-6-0；1 车负责派送零售点7，路径为0-7-0；5 车负责派送零售点1 和2，路径为0-1-2-0；3 车负责派送零售点3，路径为0-3-0。

按照遗传算法实数染色体编码规则，不影响可行解的编码采用随机排序，得出货车编码串和零售点编码串分别为：241536，467123。

解码规则同编码规则，从最终编码串中分出货车编码串及零售点编码串，在满足零售点需求且不超过每辆货车载重量的情况下对应解出所需车辆数及型号，通过零售点编码顺序确定配送顺序。

3.2 适应度函数

适应度函数是将遗传算法与待解决具体问题连接的媒介，代表种群中每个个体对所在环境的适应程度，与目标值存在对应关系。因为最终的优化目标函数为求成本最小，则定义适应度函数为目标函数的倒数[14]。为了计算本例中的是适应度，给出以

下成本计算数据。

配送距离数据（假设来回选择路径相同） 及配送等待时间数据如下：

假设整体运输中过路费50 元，根据模型中目标函数得出总费用如下：（1） 固定费用：260+350+200+260+200=1270。（2）路程成本：（20+20+10+18+25+24+24+12+30+35+15+15）×4=992。（3） 等待成本：（10+15+5+15+20+10+15+12+18+24+6+10）×3=450。总成本：50+1270+992+450=2 762。适应度为：1/2762=0.00036。

3.3 遗传算子

3.3.1 选择算子

传统的轮盘赌方式选择算子容易过早收敛，这里结合锦标赛选择法进行选择。每一次迭代中选择优秀个体，设置权重，令轮盘赌和锦标赛各选择部分个体进入下一代，能够明显增加搜索的广度。当出现算法过早收敛或早熟现象时，可选择排除非劣解进行竞争的权利，或重新洗牌来增加种群多样性[13]。

3.3.2 交叉算子

采用区域重组交叉方法改进交叉算子：随机选取位置及长度，随机排到其他解得前段，在解后部分寻找重复字符删除。例如：上文另一个可行解货车编码串及零售点编码串为：132546，537124。两个可行解交叉方式如下：

货车编码串选取的随机数为2，长度为2；零售点编码串随机数为3，长度为3。

将选中的字符串分别提到另一个可行解的开头，得到下列编码串。

将后续字符串中重复的内容去掉得到子代编码串。

3.3.3 变异算子

为了防止在迭代时陷入过早收敛或早熟情况，当种群中个体适应度差异小趋于局部最优时，增加变异概率，种群适应度发散时可减少变异概率，防止优良基因不能良好的遗传。可用下列可变变异概率来实现自适应变异算子：

If（个体适应度＞平均适应度）then Pm取值很小（0.002） 或为零；

Else Pm取值相对很大（0.08）。

可以较好地防止过早收敛或陷入局部最优，还可以防止优良基因被破坏。

4 算例分析

P 市X 区有猪肉屠宰场ZJ 厂，负责该区大型商场的冷鲜猪肉供应。共需配送的商场有20 个，分别为YYC 商场、XL 商场、WD 商场、SN 商场、HX 商场、YH 商场等。现该猪肉屠宰场冷藏运输车为同一型号，最大载重量1.5t。ZJ 市场坐标为（2745，4032），该地区生鲜肉需求点集合及各零售点坐标如图2、表3 所示。

ZJ 物流中心冷鲜猪肉平时的配送均为人工安排，现通过遗传算法优化，设置种群规模为100，交叉概率为0.75，变异概率为0.1，最大迭代次数为200，共动用冷藏货车5 辆，人工车辆调度与算法优化后路径及成本对比如表4 所示，由于实时路况无法获得数据，暂不考虑等待时间成本，假设所选择的路径均为城市路径，无收费路径，设单位运输成本为5 元/km。

MATLAB 仿真轨迹及寻优过程如图3 所示。

通过上述求解可以看出，人工安排和遗传算法求解对比，可以发现所需要的货车数量减少2 辆，每次配送成本下降近30%，优化结果良好。从左边优化过程可以看出，经过几次局部最优后通过变异等方式脱离了局部最优最终达到了全局最优，说明算法有效。

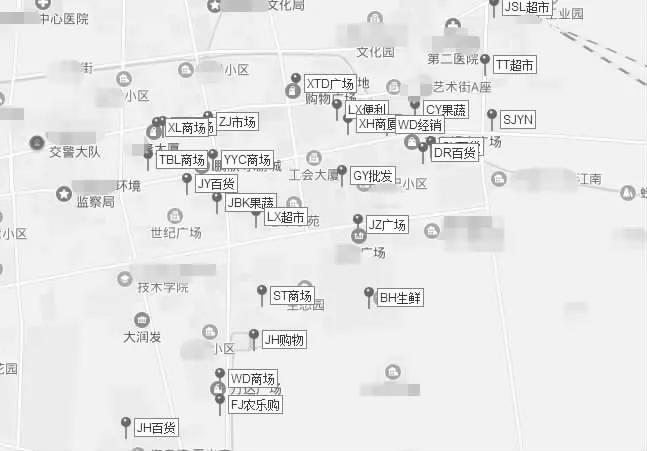
图2 该地区生鲜肉需求点集合

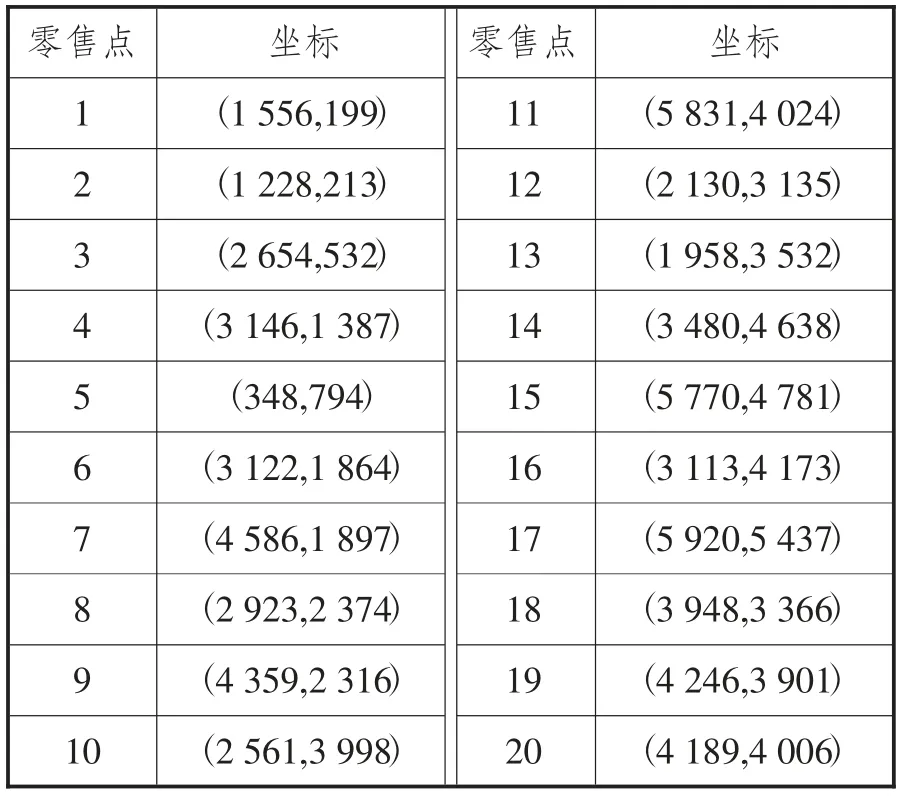
表3 各零售点坐标

表4 优化前后车辆配送信息

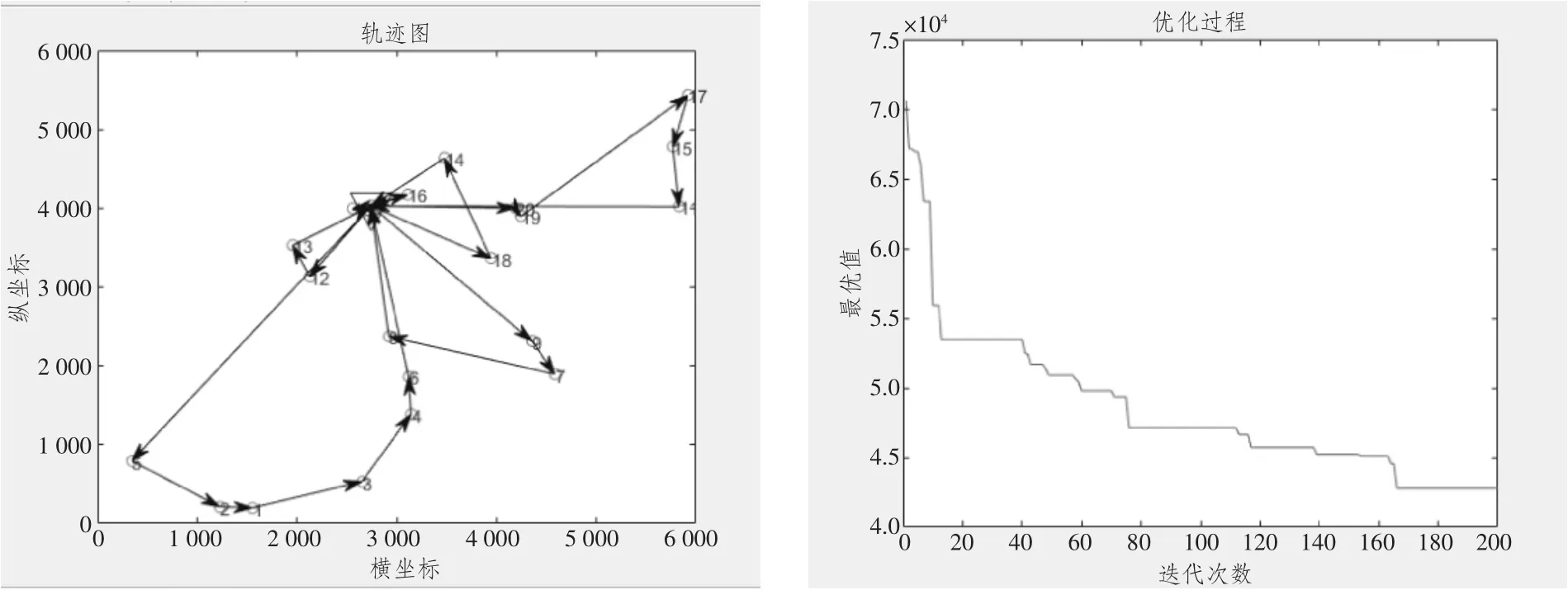
图3 MATLAB 仿真轨迹及寻优过程

5 结 论

本文提出了考虑实时路况的多车型多种类生鲜农产品配送模型，为了更好地表达多品种的思想，将厢货车按照载重量分成相等隔厢，将每个零售点需求量采用隔厢数量的方式表达，较好解决了现实中生鲜产品多产品配送问题。运用改进选择算子遗传算法对算例进行求解，说明MATLAB 仿真后得出的优化结果比人工调度成本降低了近30%，同时配送需求的货车减少了2辆，减少了物流中心固定成本的投入，为现实生鲜农产品配送提供了一定的决策依据。