面向震灾的应急救援物资调配模型研究

赵明雪，毛雪岷，章 震 ZHAO Mingxue， MAO Xuemin， ZHANG Zhen

（合肥工业大学 管理学院，安徽 合肥230000）

0 引 言

全球气候目前呈现不断变化的趋势，各种重大灾害事件频频发生，严重阻碍了我国社会经济的发展。应急管理部和国家减灾委办公室联合多部门对2018 年全国自然灾害情况进行了讨论分析，经核定，2018 年我国各类自然灾害共造成全国1.3 亿人次受灾，589 人死亡，46 人失踪，524.5 万人次紧急转移安置，直接经济损失2 644.6 亿元[1]。尤其是这些年地震带来巨大的损失，其中包括人民基本身命安全和财产的损失。如：2008 年5 月12 日四川汶川、北川发生8.0 级地震，地震造成69 227 人遇难，374 643 人受伤，17 923 人失踪。2010 年4 月14 日青海省玉树藏族自治州玉树县发生7.1 级地震涉及玉树州6 个县19 个乡镇，此次地震造成2 698 人遇难、270 人失踪。由此可知，地震灾害严重威胁了我国社会经济发展和人民生命财产安全，同时国家减灾部门在应急救灾方面也面临着重大挑战[2]。

在地震发生后，及时、准确掌握震区情况，科学有效地进行应急救援物资的调配，才能及时阻止灾情进一步蔓延。有关应急救援物资调配的问题，国内外的学者都已展开很多的研究，并且一直是公共安全、物流学等领域研究的热点之一[3]。范杰构建了基于配送时间周转量最小和物资短缺程度最小的双目标配送模型[4]。其中最关键的问题是怎样构建“最优目标数学模型”来研究应急救援物资调配模型。郭子雪等从费用最小、时间最短以及公平性的角度研究应急物资配送问题[5]。王宏伟认为决策者需要制定合理的调配方案，确保储备库中的救援物资能够顺利运达灾地区，从而减少灾害带来的损失[6]。姜海秋、Yushimito W F 等研究了自然灾害应急物资的集散地选址方法，以此确定最优的调配方案[7-8]。唐志星等研究了有限运力条件下的救灾物资调度问题[9]。Rawls C G， Tzeng G H 等对应急救助物品短期调配问题和受灾地区满意度问题进行了深入研究[10-11]。陈钢铁等研究震后应急道路抢修和应急物资配送优化调度问题，建立一个以紧急道路抢修和应急物资配送时间最小为目的多目标混合整数模型[12]。王旭坪等将受灾群众的损失用应急物资未满足率的形式量化，建立了使灾民损失和车辆调度费用最少为目标的整数规划模型[13]。在已有的研究中大多是考虑救援点到受灾点物资调配总费用最少或者运输总时间最短，很少考虑到当出现多个受灾点时，如何确定不同受灾点救援物资需求紧迫程度，从而按照应急物资需求紧迫程度的大小公平公正的合理安排应急救援物资。

地震的发生打破了受灾群众原本的生活环境，使得他们在生理和心理上产生恐慌，此时对获得的应急物资量尤为关注。因此，本文将在应急救援物资调配中引入如何确定不同受灾点救援物资需求紧迫程度的概念，构建一个运输成本最低、最大程度满足受灾点应急救援物资需求的数学模型，以芦山地震一些受灾点的数据为例采用表上作业法求解模型，以此验证模型的有效性，最后加以总结和分析。

1 构建模型

1.1 基于TOPSIS 法的多受灾点救援物资需求紧迫程度评估

理想点法的含义为根据有限个评价对象与理想化目标的接近程度进行排序的一种方法，在现有对象中进行相对优劣评价。理想化目标包括最优目标和最劣目标[14]。

由于基于TOPSIS 法的多受灾点救援物资需求紧迫程度评估误差较小，故使用此方法进行评估，具体步骤如下：

（1） 构建初始矩阵。假设有n个待评价的受灾点，m个评价因素，设受灾点i的第j个评价因素值为x ij（i=1，2，3，…，n；j=1，2，3，…，m），n个受灾点构成的初始矩阵为X。X表示如下：

（2） 构建加权标准化矩阵。德尔菲法（专家法），方法原理是集中专家知识与经验以此明确各评价因素的权重，采用Delphi 法来确定各评价因素的权重信任度较高。权重矩阵表示为将初始矩阵与权重矩阵相乘得到加权标准化矩阵B。B表示如下：

（3） 确定正负理想解。根据（1） 和（2） 得到正负理想解：

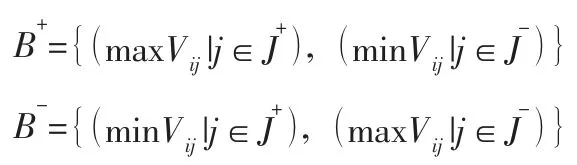
（4） 计算距离。根据欧式距离公式可知：

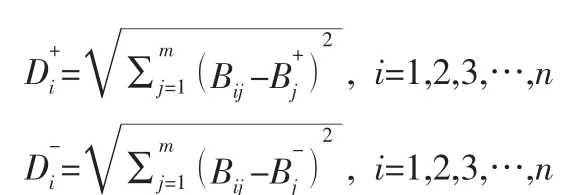
（5） 计算相对接近度并对物资需求紧迫程度大小进行排序。根据值的大小确定受灾点物资需求紧迫程度的大小对受灾点进行排序。表示如下：

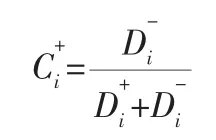
1.2 数学模型

假设某种救援物资从m个救援点Ei（i=1，2，3，…，m）运到n个受灾点Pj（j=1，2，3，…，n），cij表示从Ei到Pj的运输单价，yij表示从Ei到Pj的救援物资的数量，具体信息如表1、表2 所示。

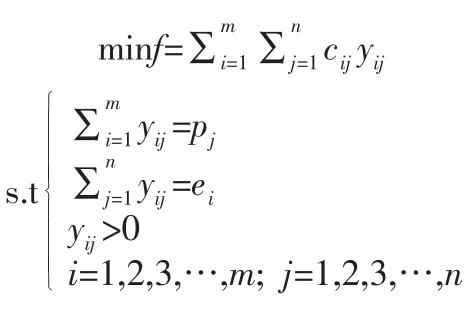
由于应急救援物资调配中还可能存在其他两种情况，第一种情况是救援物资的总量大于受灾点所需物资数量，第二种情况是救援物资的总量小于受灾点所需物资数量，而这两种情况都可以转换成上述供求相等的情况解决。

对于第一种情况供大于求，可以假设一个受灾点Pn+1，其运输单价为0，增加一个约束条件就转化为供求相等的问题，约束条件为：

对于第二种情况供小于求，我们可以假设一个救援点Em+1，其运输单价为0，增加一个约束条件就转化为供求相等的问题，约束条件为：

表1 运输问题数据表

表2 运输方案表

2 模型求解

2.1 表上作业法

上面所述的求解运输成本最低的数学模型可以看作是m×n个变量、m+（ ）

n个约束条件的线性规划问题[15]，故可用单纯形法中求解物资调配时一种经过简化的方法来求解，即表上作业法。具体求解步骤如下：（1） 画出供求平衡表。（2） 供求相等问题总有可行解，在供求平衡表里填入m+n-1 个数字格，其余非数字格为非基变量，得到初始基可行解。（3） 求解非基变量检验数，即算出表中空格的检验数。目的为：判断现在求得的解是否已经是最优解。如果是最优解，终止计算；若不是，进行下一步计算。（4） 找出换入和换出变量的空格。（5） 沿闭回路对运输数量θ 进行调整。（6） 重复步骤（3） ～（5），直到所有空格的检验数都为非负，此时得到最优方案。

2.2 确定初始解并检验

确定初始可行解一般有两种方法，最小元素法和伏格尔法。本文采用伏格尔法确定初始解。伏格尔法的计算原理可以这样解释：若一个救援点的应急救援物资不能够按照运费最小值配送，就得选择次小值，这样就形成了运费差额。差额越大代表着当不能按照最小运费调配时计算值增加越大。因此选择差额最大者，选择最小的运费向受灾点运送。具体步骤为：（1） 在表2，运输方案表的最右边增加一列ui，最下边增加一行vj，ui表示行位势，vj表示列位势。计算各行、各列最小和次小运费差额。（2） 在新增的行列中找出差额最大的，在其所在的行或者列中找到数字最小者消去该数字所在的行或者列。（3） 接着对未划去的元素计算各行、各列次小和最小运费差额，填进新加的行列中。重复（1）、（2），直到得出初始解。

对初始的运输方案进行最优性检验，可转化成对非基变量检验数σij的计算。判别最优解有两种方法：闭回路法和位势法。由于位势法步骤简洁，大多数情况下都采用位势法进行判别。本文也采用位势法求解检验数。

令u1=0，由ui+vj=cij（i，j∈N），求出ui，vj。由σij=cij-（ui+vj）（i，j∈N）计算出所有检验数，若所有非基变量检验数σij非负，则达到最优。

2.3 调整初始运输方案

如果σij＜0，说明目前得到的运输方案不是运费最低的，要调整此方案，详细步骤为：（1） 在表格中，若yij的检验数小于零，则采用闭回路法调整，把yij所在格作为调入格，以此格为出发点，作一条闭回路。（2） 计算调入量θ，即在一个闭回路中，奇数数字格中的最小者，按闭回路上的正或负号，加上或减去θ，这里统称为调入量，其余数字格不变。（3） 重复（1）、（2） 直到全部非基变量的检验数σij都非负，终止计算，求得最优运输方案。

3 实例分析

经过查阅资料文献[14]、新闻专访和查询中国地震网有关信息获得2013 年芦山地震受灾点的一些数据信息，选取其中9 个受灾点进行研究得到表3 相关信息。

根据表3 信息，通过计算选择出需要救援物资紧迫程度较大的几个受灾点，把剩余受灾程度不严重的受灾点看作是救援点。这样做的原因有两个方面：一方面是这属于就近调配，能够及时快速地运送救援物资到受灾点，对安抚民心有重要意义，另一方面是能够降低运输费用，最大程度满足受灾点的应急物资需求。

计算受灾点物资需求紧迫程度，将受灾区域平均烈度乘以10，受灾人数除以1 000，经济损失除以1 亿，受伤人数除以10。采用Delphi 法，通过专家打分得到权重矩阵为= （0.3，0.2，0.2，0.3 ）。经过归一化处理，计算得到加权标准化矩阵，计算B+、B-，得B+= （0.1253，0.0990，0.1808，0.2649 ），B-= （0.0836，0.0383，0.0004，0.0015 ），计 算 各 受 灾 点 救 援 物 资 需 求 紧 迫 程 度（0.8755，0.3886，0.2666，0.0034，0.2274，0.0883，0.0651，0.1206，0 ），因此受灾点物资需求紧迫程度由大到小的排序是：芦山县、宝兴县、天全县、雨城区、浦江县、荥经县、汉源县、名山区、丹棱县。所以前4 个地区是非常急需救援物资，看作是受灾点，而其他5 个地区受灾程度较弱，将它们看作是救援点进行救援物资配送。

假设在此次地震中某种救援物资H 在救援点的储存量和受灾点的需求量（储存量与需求量不相等），以及救援点到各受灾点的单位运输成本如表4 所示。

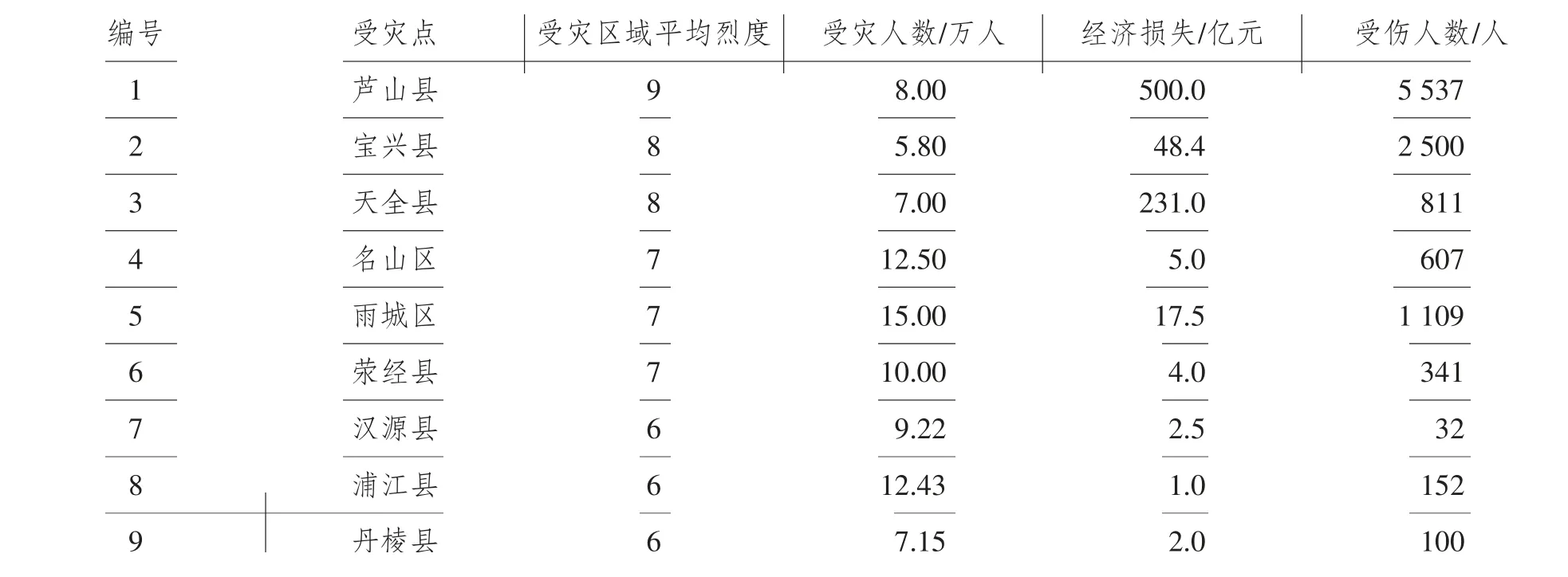
表3 受灾点相关信息

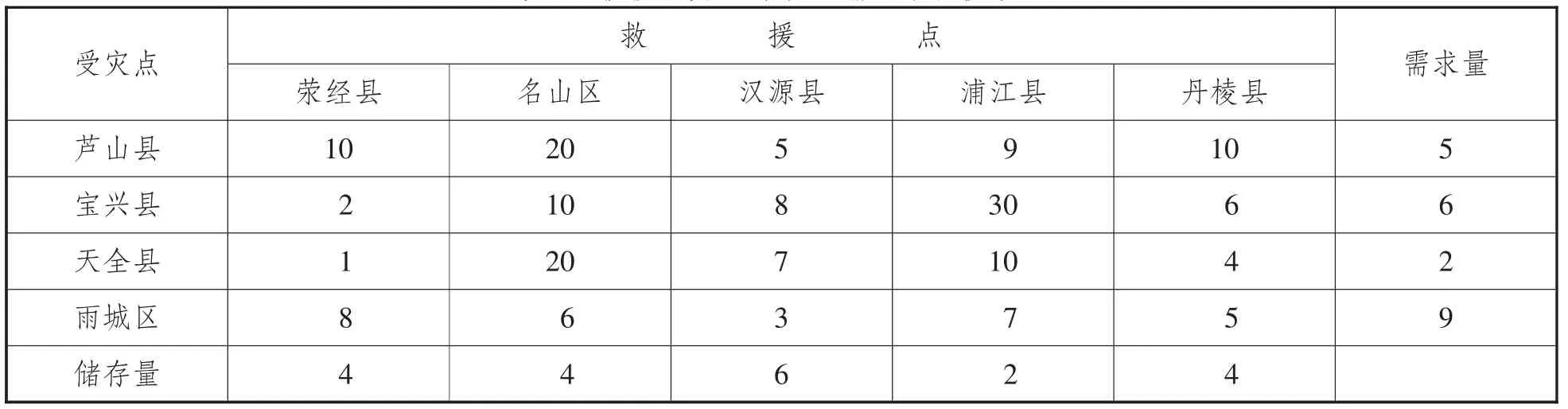
表4 救援物资H 单位运输成本和供求量

利用Lingo 软件求得救援物资H 最优运输方案如表5 所示。

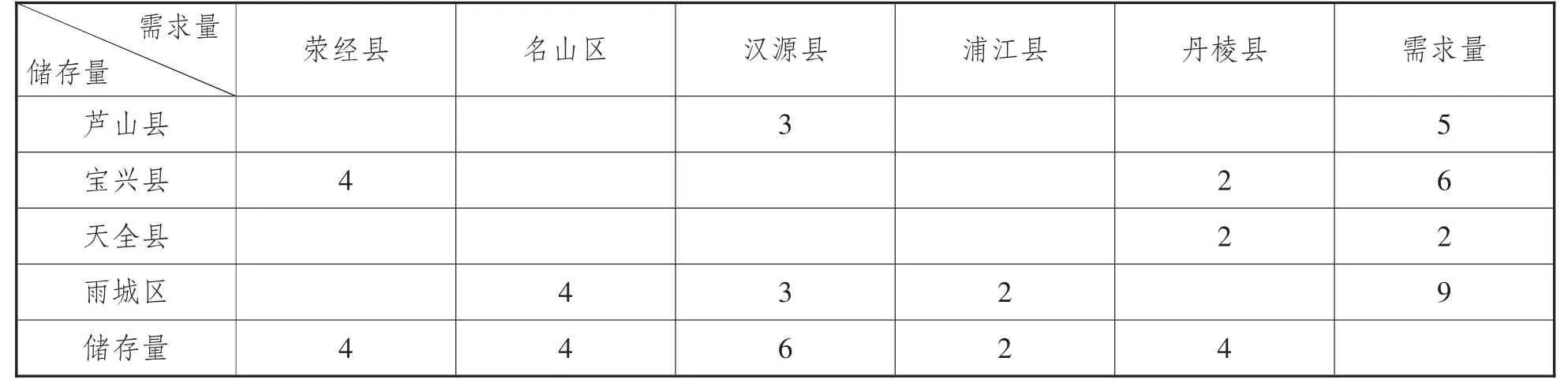
表5 救援物资H 运输方案

由于此问题有无穷多最优解，表5 所示的运输方案为其中一种，总费用为：minf=90。

4 结 论

鉴于地震的发生会带来社会各界的恐慌和不安，尤其是受灾群众。由于震级不同，不同地区的受灾程度也不同，对应急救援物资的需求量也有所不同，所以需要对受灾点救援物资需求紧迫程度进行评估。这样就可以从相邻受灾较轻地区对应急物资需求紧迫程度高的受灾点进行物资优先配送。以芦山地震一些受灾点的数据为背景设计算例，当某种应急救援物资的储存量与需求量不相等时，采用表上作业法求解该模型，通过确定初始解、对初始运输方案进行最优检验、调整初始运输方案，到最后得到总费用最小的最优运输方案。同时可以发现受灾地区的道路损毁程度和受灾点之间的地理位置也影响着最优运输方 案的选择。

由于最优运输方案的选择直接决定了应急救援物资能否及时运送到受灾地区，同时最大程度满足受灾点的应急物资需求。因此，本文首先进行基于TOPSIS 法的多受灾点救援物资需求紧迫程度评估，然后建立运输成本最低、最大程度满足受灾点应急救援物资需求的数学模型，最后的计算结果从理论和实际两个方面证明了该模型具备切实性和有效性，完成了面向震灾的应急救援物资调配模型研究。该模型为重大自然灾害应急救援物资调配方案的选择提供借鉴。本文考虑的是单个救援物资调配，由于篇幅限制没有研究多救援物资如何调配，后续学习研究中将考虑如何使多救援物资调配费用最少、时间最短，且使灾民心理满意度较高等方面问题。