关于哥德巴赫猜想

西北工业大学附中 李一霖

一、准备：(字母均表示正整数)

“一切大于等于6 的偶数，均可表示为两个质数的和‘等价于’一切大于等于3 的质数，可以表示大于等于6 的全体偶数”。以下给出几个定义及性质定理：

定义：在质数集中(设质数为an，n为质数编号，恒有an＜an+1)，将{ai}(i∈[1，n])称为n个已知质数，已知质数从质数列由小到大顺次取得(如已知2、3、5 时，{ai}增加一项只可为7)，这n个质数各自倍数集的并集A在N＊中补集称为n阶已知质数列，记为{xn}，其中n为阶数，也为已知质数数量。

二、n 阶已知质数列的性质

1.{xi}中xi+1-xi的值是循环的，循环节长度(即第m个循环节首项与第m+1 循环节首项差之绝对值)为an的阶乘。

证明：由互质知，设{ai}所有项最小公倍数为bn=an！，{ai}各项倍数集都包含kbn(kN＊)，n个倍数集均出现的数是且仅是bn的倍数集。对{xn}中任一项xi(i表示项的序数)，由最小公倍数为bn，每项xi+mbn必然也在该数列中，故{xn}每个以bn为长度的循环节内递增速度循环，n一定时，循环节固定。

2.n阶已知质数列中一项xi必然为真实质数(在正整数集中恰有两因数，即确实为质数)的充分条件是xi＜an2(an为{ai}中最大一项)。证明：设{xn}中任一项xi＜an2，分解因数得xi=p1p2……pr，(r≥2)，其中pi为质数且pi≥an，则m≥an2，这与m＜an2矛盾。故xi分解所得至少有一项pi≤an，则这样的xi应已被筛除，故任一项xi＜an2均不可质因数分解。故{xi}中取任一项xi＜an2，xi为真实质数。

3.n阶已知质数列在n递增时，逐渐筛除已知质数列各项。新增已知质数an+1，只可能筛除xi＞an2，由质因数分解得数项存在某一项pi≥an可得该性质。

4.定义{xn}在第m区间中的任一项满足xi∈( ， )。当n递增至正无穷，{xn}将趋向真实质数列。由上知，新增已知质数an+1能确定第n区间的真实质数，第n-m区间(m≥1)真实质数已由ai(i≤n)确定。

三、真实质数列与两项差数列

定义：设{xn}中两邻项xi+1、xi(i∈N＊)，取全部yi=xi+1-xi，yi由y1始顺次排列称n阶两项差数列，记为{yn}，n为阶数。

注：{xn}在m区间内所有项对应所得的{yn}，称为第m区间内的{yn}。将第二部分中的性质推广到{yn}：易知{y1}中yi=2，{y2}中有y2i-1=2，y2i=4，n给定时，{yn}各项固定，且n递增时对{xn}筛除xi，使得xi在{yn}中对应的前后两项yi与yi+1相合为一项yi+yi+1。由上可知n给定时，设{yn}的固定循环节为Yn，且n增大时{xn}中所有项xi(满足xi＞an2)对应的yi某些对邻项相合，使得其遵循循环Yn+1，且不会对xi(满足xi＜an2)对应的任一yi产生影响。

定义：k个已知质数顺次增加t个，导致第m区间内，{yk}升阶为{yk+t}，导致某些邻项相合为一项，称为t次相合。

相合性质：①在m区间内对{yk}进行t次相合，所得{yk+t}所有项之和不变，即{yk}与{yk+t}在第m区间内所有项和相同。

证明：设{yk}与{xk}中任一项yi=xi+1-xi，设{ai}中新增ak+1，即相合一次。

当m≤k-1 时，第m区间中，{xk}中任意xi＜ak2，由上，ak+1不会对{xk}及{yk}造成影响，即相合前后第m区间内{yk}所有项和相同，所有项均不变。

当m≥k时，第m区间中{xk}满足任意xi＞ak2，设{xk}中有xi+n数项(n为定值且n≥1)，对应{yk}中yi+n数项。由上性质，若ak+1筛除xi+t(t∈[2，n-1])得到xi+1、xi+n，相应地，{yk}中各项yi+n相合为yi+1+yi+2…+yi+n一项，即此时仅有{yk}所有项相同。相合1 次可递推至t次。

定义：展开是相合的逆向变形，在第m区间中k个已知质数由大到小减少t个，每次减去最大一项，使得{yk}降阶为{yk-t}，称为对{yk}t次展开。

展开与相合证明同理，其性质为：对第m区间内{yk}t次展开，所得{yk-t}在该区间内各项和不变，m≤k-t-1 时，各项相同，m≥k-t时，部分项各自展开为和不变的一列顺次排列的项，代替原数位置。

两项差数列及其循环节的性质：由{yk}升阶为{yk+1}，循环节长度变为原本的ak+1倍，其性质如下：①记{yk}循环节为Yk，由上，Yk+1为Yk重复ak+1次并对某些项相合所得，且Yk+1中相邻两个Yk中相合的两项在各自所在Yk中所处位置不同(yi到自身所在的循环节Yk首项间所有项之和看作yi在循环Yk中的位置)。

证明：设{xk}循环节长度为bk=ak！，又设{xk}与{yk}中yi=xi+1-xi，当{xk}升一阶，{ai}中新增ak+1使得xi被筛除，使得{yk}中yi-1与yi相合。由Yk长度为bk，故{xk}中，xi在下一个循环节相同位置的数为xi+bk(xi丨ak+1)，由bk与ak+1互质，又ak+1丨xi，故xi被筛除时，xi+bk不被筛除。经递推，其对t次相合同样适用。

四、等价命题证明

定义：从{xn}中选取一个固定的数q，称为基数，q顺次加上{xn}所有项，所得数列称为基数x的n阶基数和列，记为{zn}=q+{xn}。

由数学归纳法：当{an}中n=1 时，{x1}中任一项xi=2i-1，{yi}中任一项yi=2。取{x1}中3 为q1，q1+{x1}=2i+2，又i∈N＊，故{x1}中取两数可表示一切质数ai(ai≥6)，但所取两数不一定均为质数。

当{an} 中n=2 时，{x2} 任 一 项x2i-1=6i-5，x2i=6i-1，{y2} 任 一项y2i-1=4，y2i=2， 以3 为q1，q1+{x2} 中z2i-1=6i-2，z2i=6i+2. 与正偶数列相比，6i+4 未表示，更换基数q2=5，q2+{xn}为z2i-1=6i，z2i=6i+4，则6i+4 得到表示，则在{x2}中取两项求和可表示6 以上全体偶数。

故若能证明“在已知质数筛除过程中，基数q的m阶基数和列中每一个筛除的偶数均可通过更换基数得到表示”，则“一切大于等于3 的质数，可以表示大于等于6 的全体偶数”。下述证明过程通过图形理解为(下行为上行邻项差)：

{xk}：q3→q3+d…xi+1-d←xi+1、xi+2、xi+3

{yk}：…d………………d、yi+1、yi+2

证明如下：设yi=xi+1-xi，对于给定的k，设{xk} 中有三项xi+m(m∈[1，3])，在{yk} 中 对 应 两 项yi+m(m∈[1，2])，当{ai} 中新增ak+1，使得xi+2被筛除，则升阶前基数q3与xi+2相加所得偶数xi+2+q3，升阶后xi+2+q3无法表示，不妨设xi+2≥q3。在{xk}中，取整数d，使得xi+2-d也在{xk}中，对应地，{yk}中取得顺次相邻数项yi+n(n≤1)其和也为d，将和为d的这部分项yi+n记为A。记q3位于第r-1区间，是{xr}的一项。将A在和为d不变时，经过k-r次展开得{yr}相同位置的对应部分D，可能有部分项各自拆分为两邻项。D是Yr的一部分，与{yr}中每个循环节相同位置的数项完全重合，由此可在D不变的前提下转移D在{yr}中所在的循环节，但在各自循环节中位置固定。设D首项为s，转移D在{yr}中所在的循环节，使q3与q3在{xr}中下一项之差为s，即使得在{xr}中q3对应{yr}中的s。这一过程可行性后文论证。用q3顺次加上D的所有项，可知q3+d存在于{xr}。故q3+d在{xr}中，xi+2-d在{xk}中，由xi+2≥q3，q3所在区间不高于xi+2所在区间，由性质知r与k充分大时，存在d使得q3+d、xi+2-d均在{xk}中，即从{xk}中，取q3+d、xi+2-d相加可得偶数ak+1+x。k增大时，重复执行该过程，使得由筛除而无法表示的偶数得到表示。

论证以上内容中的q必然可以取到，如下：对于给定基数q，{xk}升一阶后筛除的质数ai+2，不妨设x≤ai+2，设q位于第r-1 区间，是{xr}中一项，设{yr}循环节为Yr，有r≤k。如下图，一个Yr循环用相邻两条“丨”之间所有项表示，将{yr}升阶为{yk}，由相合性质得相邻两竖线间的各项和相等，故设n表示各自所在循环节的第n项，且规定：若n项前有邻项相合，该项的序号n不变，即项数相同时，该项所在循环节中该项前所有项和相同，即位置相同。nm表示第m个循环的第n项。下图每两行为一横行，一行为{yr}，第二行为对应的{xk+1}，↓下方为箭头左右两项之差。

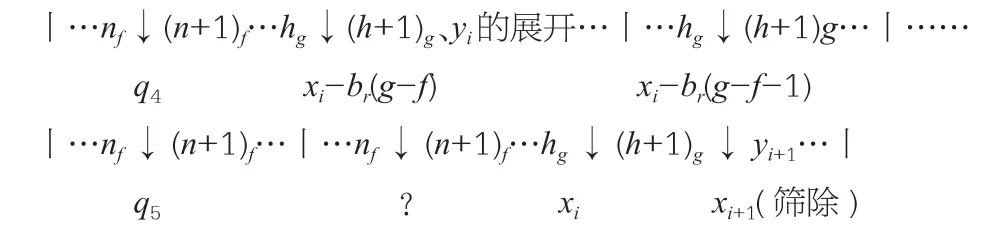
设循环节长度为br=ar！，设图中首个循环节为第f个，末尾为第g个。第g个循环节中hg、(h+1)g两项在第f个循环节中可找到相同位置完全相同两项，或相邻三项(或以上)可相合后变为hg、(h+1)g两项，故将hg、(h+1)g转移至第f个循环中，得到相同位置两项或以上的相合.不妨设所得项在nf、(n+1)f后方，如图所示，其对应{xk+1}中项为ak-br(g-f)，若取△1=xi-br(g-f)-q4，△代表{yr}中q4至xibr(g-f)所有项之和，将△1转移至第g个循环中从(h+1)g向前排列，且由相合性质可保证在和不变时(项可能相合)但项数均不变，在第g个循环中，△1排列得nf.(n+1)f.但由于f到g所在区间提高，新增质数可能导致？处质数被筛除，需讨论：①nf、(n+1)f之间的质数未被筛除，则△1作为③中的d，xi-br(g-f)作为新基数，？处的质数与新基数相加，最终表示筛除的偶数xi+q4。②nf、(n+1)f之间质数被筛除，则将hg、(h+1)g转移到第f+1 个循环，如图，同理得△2，将△2转移至g与g-1 个循环节中，若第g个循环节中？处质数被筛除，则第g-1 个循环节中，相同位置两项nf、(n+1)f不会进行相合，则此时q5必存在于{xk+1}中，可见③中d必然可以取到。

综上，由数学归纳法得“在{ai}中项增多，即{xn}被筛除过程中，{zn}中每个被筛除的偶数均可通过更换q表示”，即有“一切大于等于3两个的质数之和可以表示大于等于6 的全体偶数”，等价于“一切大于等于6 的偶数，均可表示为两个质数的和”，证毕。